算法合集之《浅谈部分搜索+高效算法在搜索问题中的应用.pdf

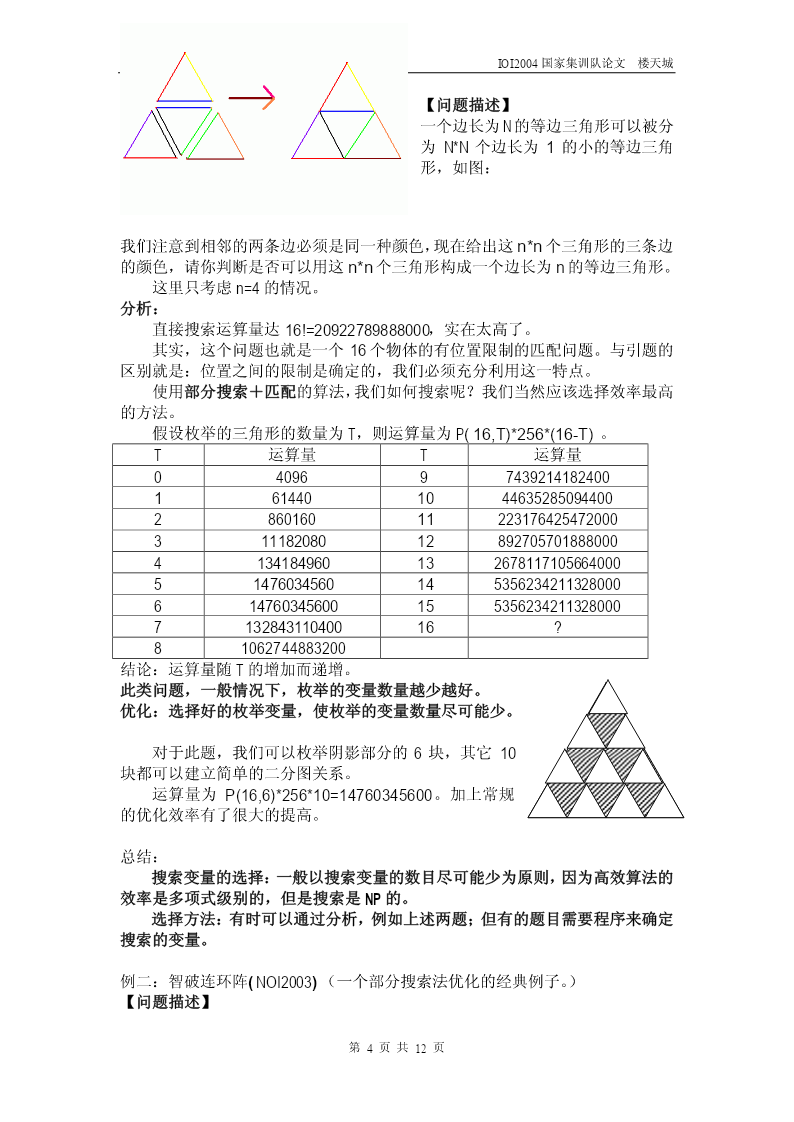
IOI2004国家集训队论文楼天城

浅谈部分搜索+高效算法在搜索问题中的应用
浙江省杭州第十四中学楼天城

摘要：
本文从有位置限制的匹配问题的搜索谈起，通过对题目MilkBottleData的
分析，提出了深度优先搜索的一种非常规搜索——部分搜索+高效算法。然后通
过部分搜索在TriangleConstruction和智破连环阵两题中的应用，探讨了部分搜
索方法通用的主要优化方法，并从此方法本质分析其高效的原因所在和应用需要
满足的要求和限制。
关键字：
部分搜索、高效算法
正文：
很多题目，如果我们可以建立数学模型，应该尽量用解析法来处理，因为简
单的模型更清晰地反映了事物之间的关系。
但是，并不是所有的题目都可以建立简单的数学模型。我们这时必须使用搜
索的方法，也就是枚举所有可能情况来寻找可行解或最优解。
由于搜索建立在枚举之上，所以搜索常常和低效是分不开的。有时搜索的运
算量实在太大，实在是一件痛苦的事情。
于是我们需要利用很多技巧来提高效率，可行性剪枝，最优性剪枝和调整搜
索顺序等方法都很有用，在它们的帮助下，我们可以大大提高搜索的效率。
而有些题目，这些常规的优化方法很难有用武之地。这是我们必须使用一些
非常规的搜索方法。本文中我们将讨论非常规搜索中的一种——部分搜索+高效
算法。

引题：
N个物品与N个位置，给定每个物品的可能放的位置集合，要求寻找一一
对应的关系，但还给出物品位置之间的限制（例如：如果1放在3则2不能放在
1），求一组可行解，或给每一种对应关系一个权，求满足条件的最优解。
由于事物之间的限制关系非常复杂，很难建立简单的二分图关系，或者用网
络流来解决。
面对这一系列类似的问题，我们一般只有搜索，如何搜索又如何优化呢？

简单分析：
如果我们枚举每一个物品的位置，然后判断，这样的时间复杂度为O(N!)。
好像似乎也只能这样。

进一步分析：
我们看一个例子，N=6：
其它限制有4条(a,b,c,d)表示如果a放在b则c不能放在d
1356
2253
3141
3262

IOI2004国家集训队论文楼天城

后来我们发现，如果我们一旦确定了3和5的位置，其它4个物品的位置之
间已经没有限制关系了，这样其它4个物品的位置可以通过匹配来解决。
这时我们可以发现一个新的搜索模式：部分搜索。
部分搜索：搜索一部分变量，使得余下的变量之间的关系简化，然后通过
一些高效算法（一般有匹配、解方程、贪心、动态规划等）完成余下问题。
就本题而言：先搜索一定数量（而不是全部）的物品的位置，使问题内物品
的关系简化为二分图关系，用二分图匹配来解决余下的物品。
本质：
其实，例如上面的例子，如果我们先知道了3和5的位置后，不用匹配，其
实我们是在用搜索来求匹配，效率当然不会高。
通过部分搜索为其它高效算法提供条件（例如上面的例子创造二分图关
系），而其它高效算法代替搜索，高效地完成余下的任务。
部分搜索的方法充分发挥了搜索和其它高效算法的优势。搜索的优势在于
应用性广，可以克服复杂的情况，其他高效算法的优势在于效率高。两者相互
促进，同时也弥补对方的不足。这也是这个方法的成功的关键。
部分搜索+其它高效算法已经在很多题目中得到了应用。我们通过几个例子
来探讨这种搜索方法的应用和优化技巧。

先看一个应用的例子。
MilkBottleData(ACM/ICPCAsiaRegionalShanghai1996)
【问题描述】
一个被分为N*N个网格的盒子，每一格有可能包含一瓶牛奶或者什么都没有。
史密斯先生对每行从左到右记下牛奶的情况，同样对每列从上到下记下牛奶的情
况。每一条记录包含N的数字，0表示没有牛奶，1表示有牛奶。不幸的是，2*N
条记录的顺序被打乱了，有些数字也模糊不清。
现在史密斯先生请你恢复原来盒子的牛奶情况。
输入：
第一行：一个整数N，然后的2N行，每行有N个数字，0表示一定没有牛奶，1
表示一定有牛奶，2表示不能确定。
样例：
input
5
01210
21120
21001
12110
12101
12101
00011
22222
11001
10010
output
98627

IOI2004国家集训队论文楼天城

410110
1010010
101110
301001
511101
数据范围：1<=N<=10
初步分析：
行列之间的限制关系非常复杂，很难找到多项式算法。（网络流！？）
可以用(2N)!的深度优先搜索，依次枚举每行和每列的记录编号，然后判断
是否产生了矛盾。
判断方法：
设：第i条记录的第j个数字为A[i,j]。
如果第a行选择第x条记录，第b列选择第y条记录，那么矛盾的条件就是：
((A[x,b]<>2)and(A[y,a]<>2)a