ch6 Bézier曲线与曲面.ppt

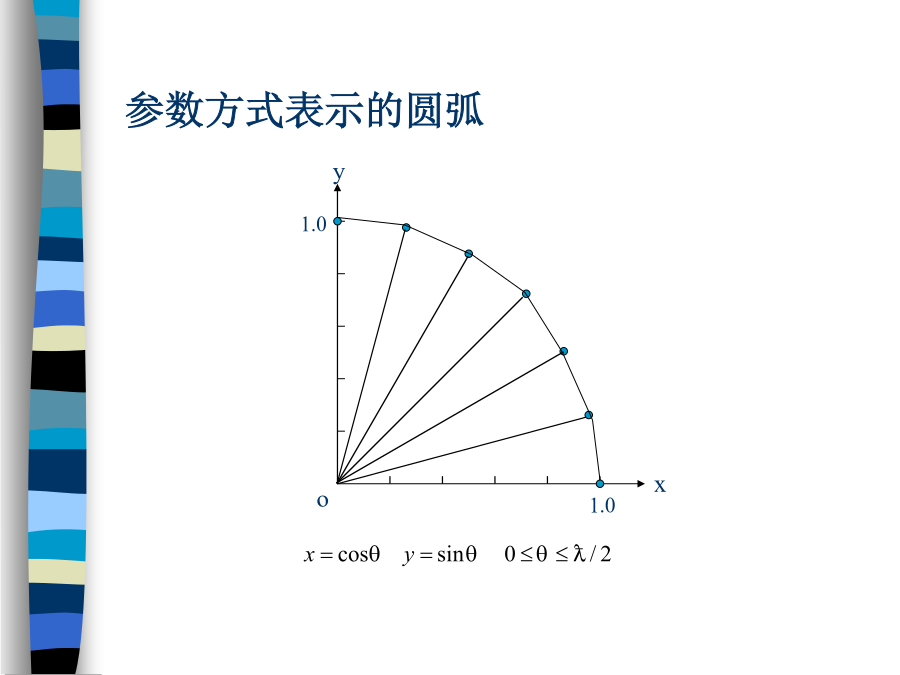
计算机图形学曲线和曲面1：曲线、曲面研究的发展过程1972年，德布尔(deBoor)给出了B样条的标准计算方法；
1974年，通用汽车公司的戈登(Gordon)和里森费尔德(Riesenfeld)在B样条理论的基础上，提出了B样条曲线、曲面；
1975年，美国的佛斯普里尔(Versprill)提出了有理B样条方法；
80年代后期，美国的皮格尔(Piegl)和蒂勒(Tiller)将有理B样条发展成非均匀有理B样条(NURBS)方法；2.曲线、曲面参数表示的基础知识2.1显式、隐式和参数表示隐式表示
隐式的非参数方程一般形式为：f(x,y)=0；如二阶隐式方程的一般式可写成：

通过定义不同的方程系数a,b,c,d,e,f，即可得到不同的圆锥曲线，如抛物线，双曲线和椭圆等。参数表示
在平面曲线的参数表示中，曲线上每一点的坐标均要表示成一个参数式。如用参数t表示，则曲线上每一点坐标的参数形式是：

曲线上一点坐标的矢量表示是：

如用`表示对参数的求导，则参数曲线的切矢量或导函数是：y参数方式表示的圆弧参数方式表示的圆弧参数表示的优点2.2参数曲线的定义及切矢量、曲率切矢量曲率2.3插值、逼近、拟合和光顺线性插值线性插值抛物线插值(2)逼近最小二乘法解决逼近问题最小二乘法解决逼近问题(3)光顺(4)拟合2.4参数曲线的代数形式和几何形式几何形式表示几何形式表示2.5调和函数2.6曲线段的连续性定义曲线段的连续性曲线段的连续性3.Bézier曲线和曲面Bézier曲线的定义和性质Bezier曲线示例Bernstein基函数性质Bernstein基函数性质Bernstein基函数性质Bezier曲线的性质Bezier曲线的性质Bezier曲线的性质Bezier曲线的性质Bezier曲线的性质Bezier曲线的性质Bezier曲线的性质