高斯光束及其传播特性的仿真.ppt

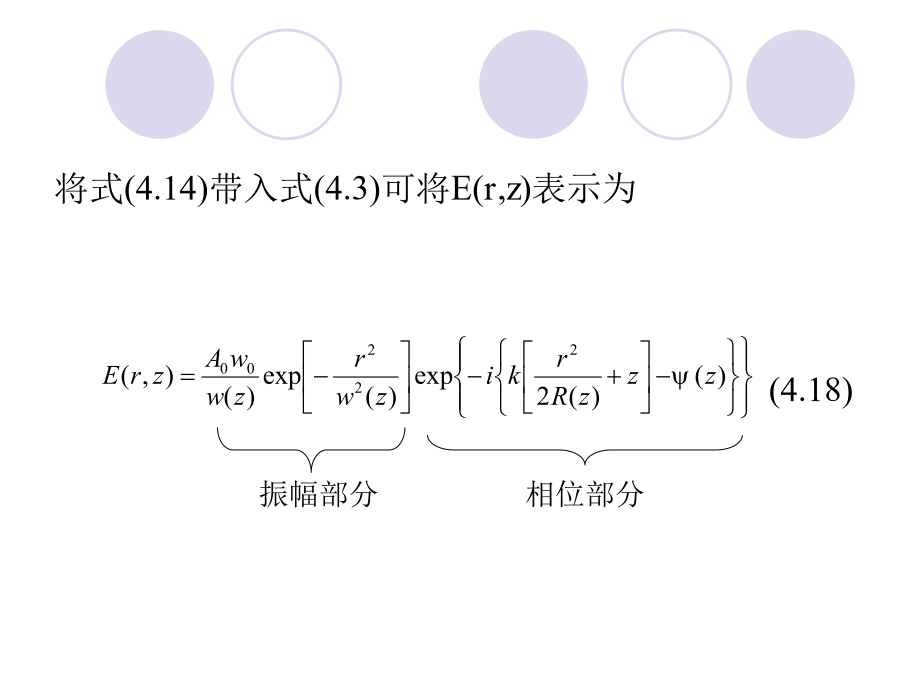
高斯光束及其传播特性的仿真高斯光束的基本性质式(4.13)可改写为

(4.14)
式中，w(z)为高斯光束的束宽，R(z)为高斯光束的等相面曲率半径，Ψ(z)为高斯光束的相位因子，表达式分别如下：

(4.15)
(4.16)
(4.17)将式(4.14)带入式(4.3)可将E(r,z)表示为

(4.18)
高斯光束的复参数表示和ABCD定律这样高斯光束可由复参数q确定。当q已知时，R(z)、w(z)可按下式求出：

(4.30)

(4.31)
其中，Re表示复数取实部；Im表示复数取虚部运算。
2、高斯光束的ABCD定律
高斯光束复参数q通过变换矩阵的光学系统的变换遵守ABCD定律：

(4.32)
如果复参数为q的高斯光束顺次通过变换矩阵M1、M2，…，Mn的光学系统后变为复参数为q的高斯参数，利用矩阵乘法易证，此时ABCD定律亦成立。
当q和M1、M2，…，Mn为已知时，原则上由ABCD定律可求出任意z处的q，再由式(4.30)和(4.31)做复数运算分离实部和虚部得到R和w。
现在以高斯光束在自由空间传输为例说明ABCD定律的应用。设在z=0处有一等相面为平面的高斯光束：

(4.37)
在自由空间中传输距离z后，设其复参数为q。因为自由空中的传输矩阵为，由ABCD定律可得

(4.39)将(4.27)、式(4.37)代入式(4.39)中做复数运算，可以得到

(4.40)

(4.41)
高斯光束通过复杂光学系统的变换实际工作中最感兴趣的是X1=X2=0，即研究入射与出射高斯光束束腰间的变换问题，此时式(4.46)简化为

(4.49)

当n2=n1=1时，式(4.49)可写成

(4.52)

高斯光束通过薄透镜的变换项目一：根据高斯光束的特性，在MATLAB中作出束腰半径为0.5mm的高斯光束在束腰处的三维光强分布图。
项目二：在MATLAB中编程，作出高斯光束在通过薄头镜变换时，取不同的归一化参数Z01/f（0,0.2,0.4,0.5,1.5）的情况下，归一化物距参数s0/f随归一化像距参数si/f的变化曲线。
项目三：作出物象比例wi/w0和归一化物距s0/f的关系曲线。