高斯光束的matlab仿真.pdf

高斯光束的matlab仿真

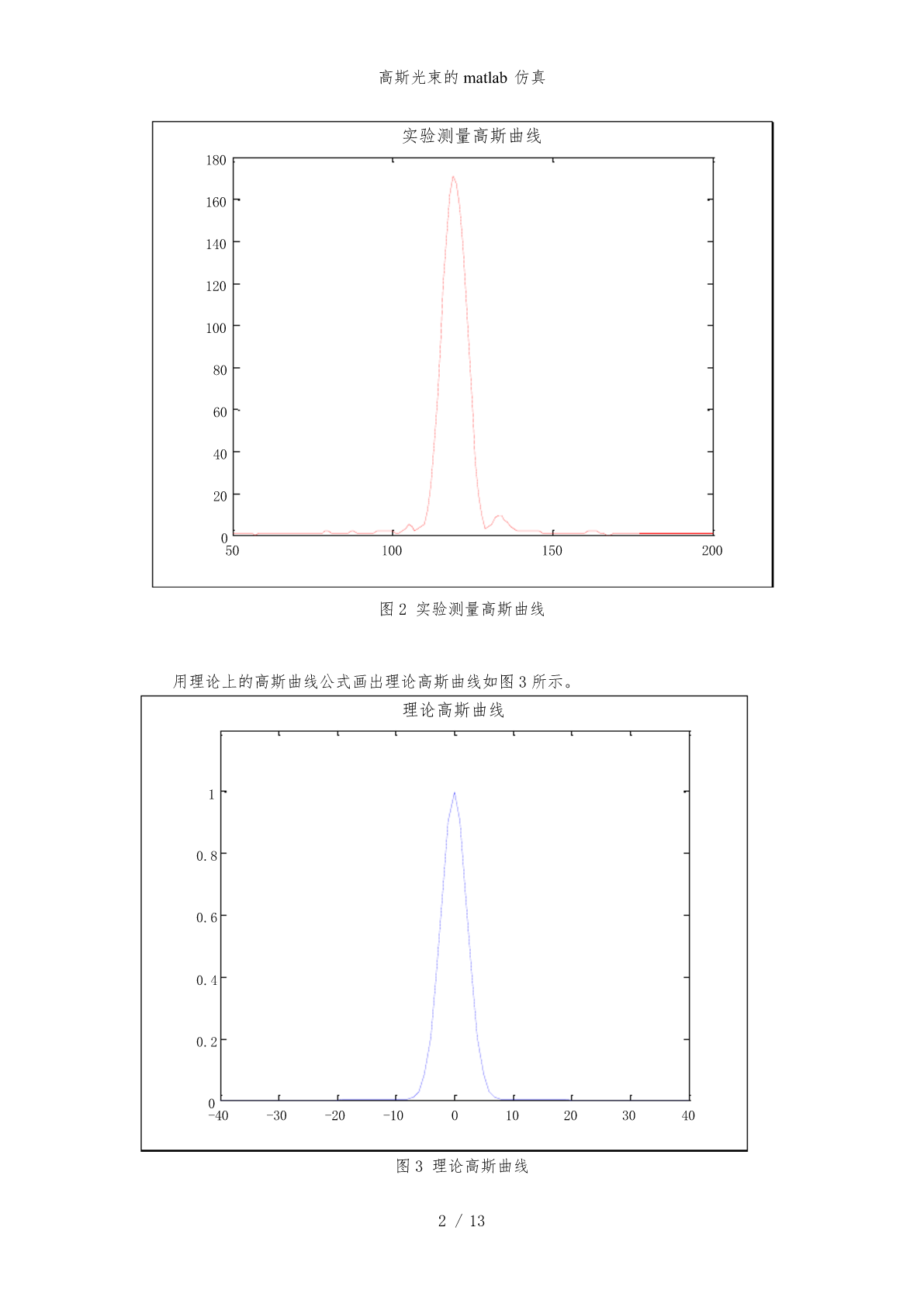
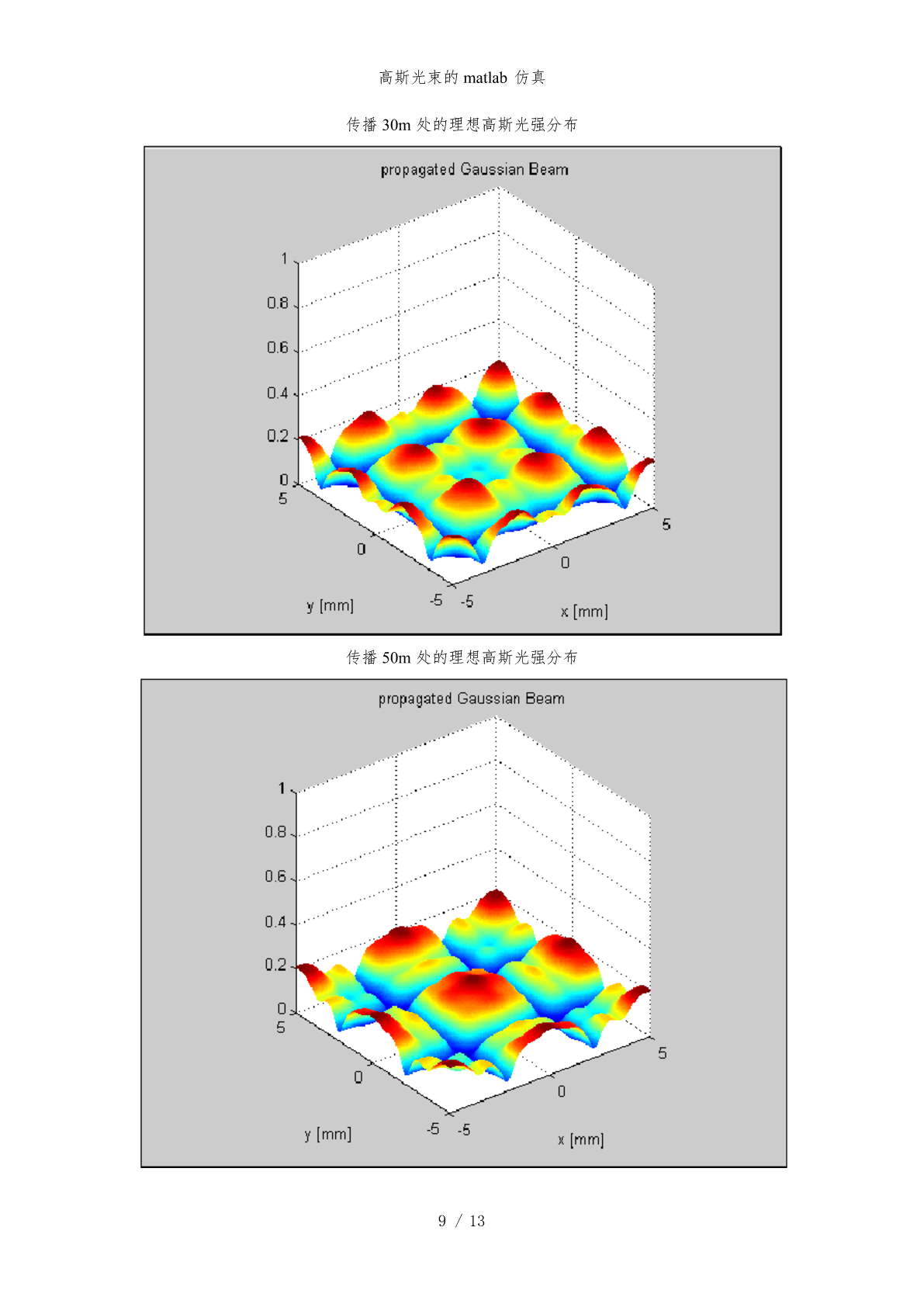
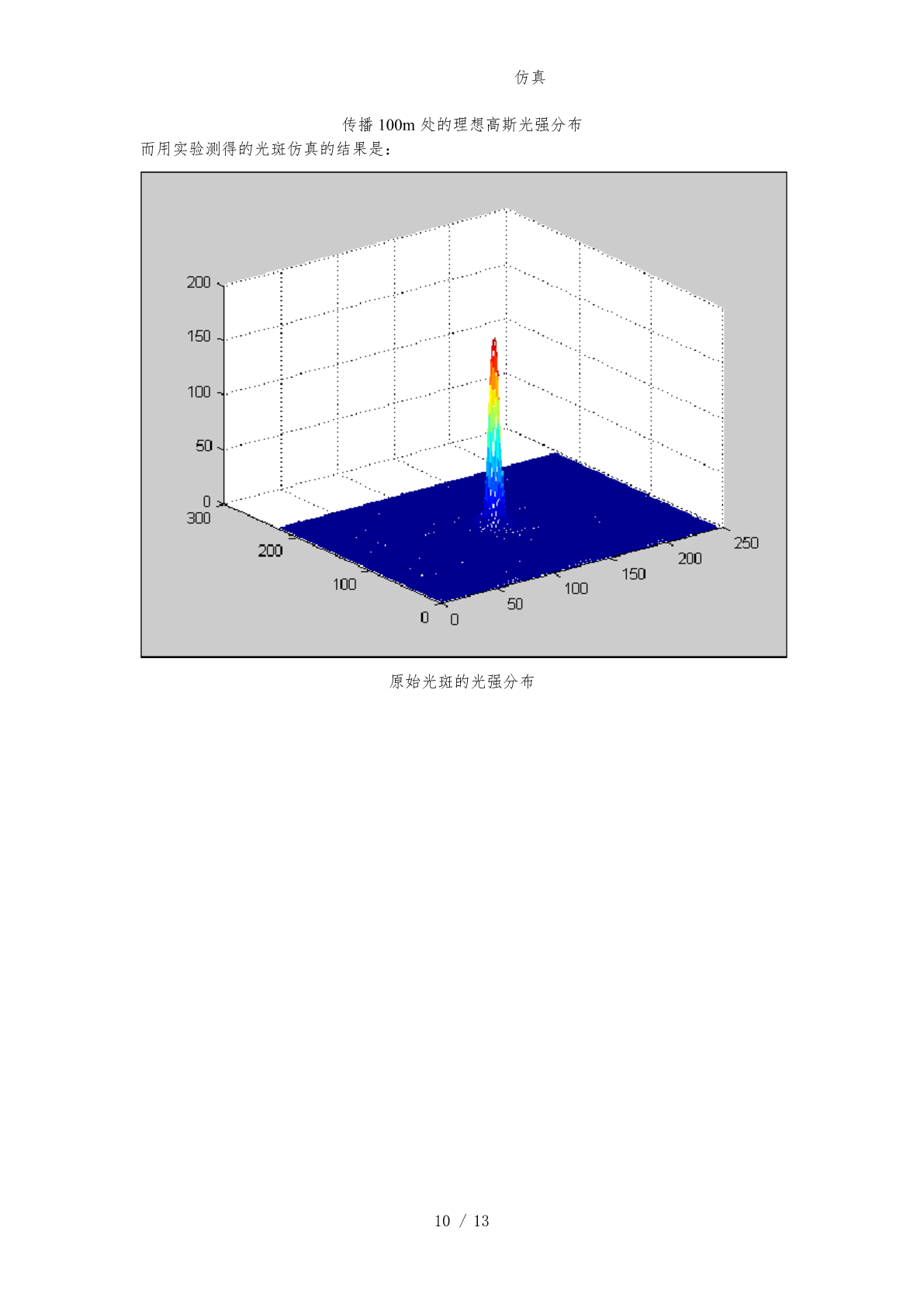
题目：根据高斯光束数学模型，模拟仿真高斯光束在谐振腔中某一位置处的归一化强度分布

并给出其二维、三维强度分布仿真图；用Matlab读取实际激光光斑照片中所记录的强度数

据（读取照片中光斑的一个直径所记录的强度数据即可，Matlab读取照片数据命令为imread）,

用该数据画出图片中激光光斑的强度二维分布图，与之前数学模型仿真图对比。（如同时考

虑高斯光束光斑有效截面半径和等相位面特点，仿真高斯光束光强、光斑有效截面半径以及

等相位面同时随传播距离z的变化并给出整体仿真图可酌情加分。）

原始光斑如图1所示，用imread命令读入matlab后直接用imshow命令读取即可，

CCD采集的高斯光束光强分布

图1CCD采集的高斯光束强度分布

读入的数据是一个224X244的矩阵，矩阵中的数值代表光强分布。用读入的数据取中间一
行（122行）画出强度分布如图2所示。

1/13
高斯光束的matlab仿真

实验测量高斯曲线
180

160

140

120

100

80

60

40

20

0
50100150200

图2实验测量高斯曲线

用理论上的高斯曲线公式画出理论高斯曲线如图3所示。
理论高斯曲线

1

0.8

0.6

0.4

0.2

0
-40-30-20-10010203040

图3理论高斯曲线

2/13
高斯光束的matlab仿真

M文件如下：
A=imread(作业激光原理与应用高斯.bmp');
A1=A(:,122);
x1=1:1:224;
x2=-100:1:100;
a2=exp(-x2.^2/10);
figure
imshow(A);
axisoff
title('ontsize{12}CCD采集的高斯光束光强分布');
figure
plot(x2,a2,'linewidth',1,'color','b');
axis([-404001.2])
title('ontsize{12}实验测量高斯曲线')
figure
plot(x1,A1,'linewidth',1,'color','r')
title('ontsize{12}理论高斯曲线')
axis([502000180])

画三维强度分布。取图片矩阵的中间层，用mesh命令画出三维图如图4所示。

图4三维强度分布
由于读入的图片有一行白边，需要手动去除掉，否则三维图会有一边整体竖起来，影响观察。
最终的M文件如下。
作业激光原理与应用高斯.bmp');
[high,width,color]=size(A);
x=1:width;
y=1:high-1;
mesh(x',y',double(A(2:224,:,1)));
gridon
xlabel('x'),ylabel('y'),zlabel('z');

3/13
高斯光束的matlab仿真

title('三维强度分布');

再用matlab仿真理论上传播过程中高斯光束的变化
这次先给出M文件：
%Gaussian_propagation.m
%SimulationofdiffractionofGaussianBeam
clear;
%GaussianBeam
%N:samplingnumber
N=input('Numberofsamples(enterfrom100to500)=');
L=10*10^-3;
Ld=input('wavelengthoflightin[micrometers]=');
Ld=Ld*10^-6;
ko=(2*pi)/Ld;
wo=input('WaistofGaussianBeamin[mm]=');
wo=wo*10^-3;
z_ray=(ko*wo^2)/2*10^3;
sprintf('Rayleighrangeis%f[mm]',z_ray)
z_ray=z_ray*10^-3;
z=input('Propagationlength(z)in[mm]');
z=z*10^-3;%dx:stepsize
dx=L/N;
forn=1:N+1
form=1:N+1
%Spaceaxis
x(m)=(m-1)*dx-L/2;
y(n)=(n-1)*dx-L/2;
%GaussianBeaminspacedomain
Gau(n,m)=exp(-(x(m)^2+y(n)^2)/(wo^2));%Frequencyaxis
Kx(m)=(2*pi*(m-1))/(N*dx)-((2*pi*(N))/(N*dx))/2;
Ky(n)=(2*pi*(n-1))/(N*dx)-((2*pi*(N))/(N*dx))/2;
%Freespacet