内容提供者
二次函数y=ax²＋k的图像和性质.ppt
2024-08-19
10金币
903KB
9页
dc****76
实名认证
内容提供者
1/9
2/9
3/9
4/9
5/9
6/9
7/9
8/9
9/9
在线预览结束，喜欢就下载吧，查找使用更方便
相关资料
二次函数y=ax²＋k的图像和性质.ppt
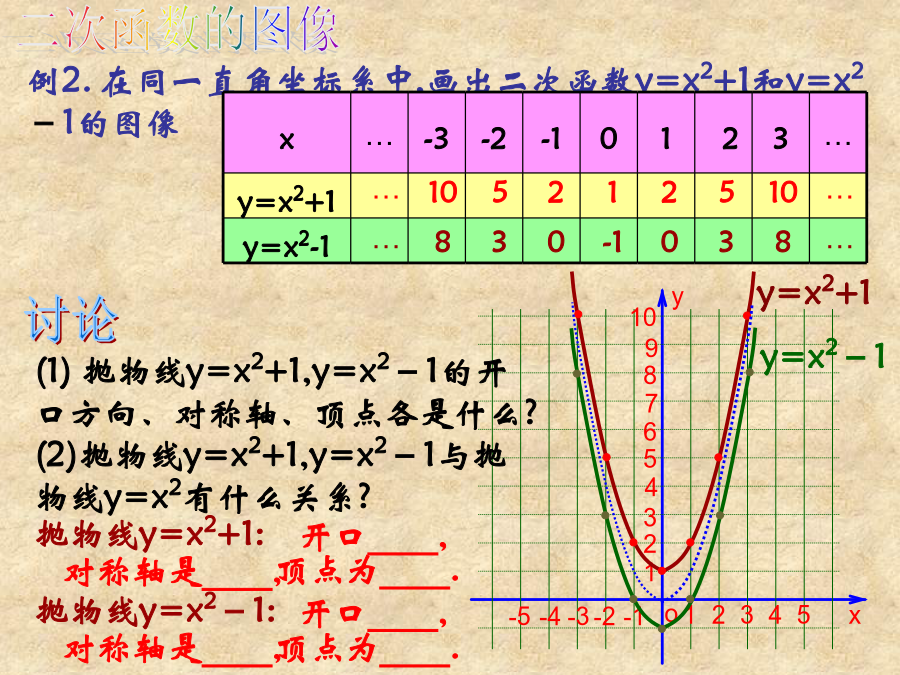
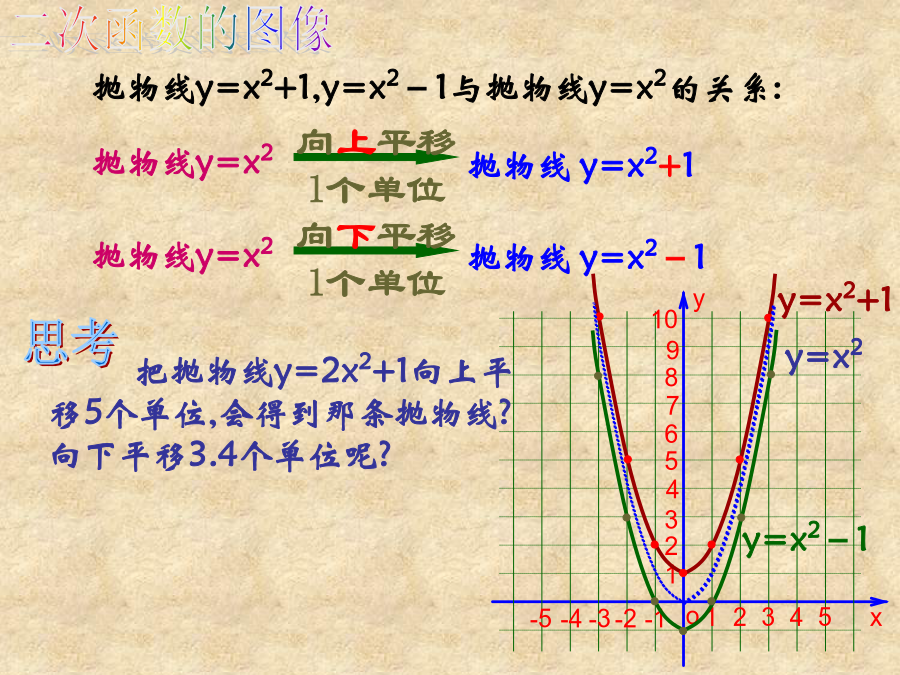
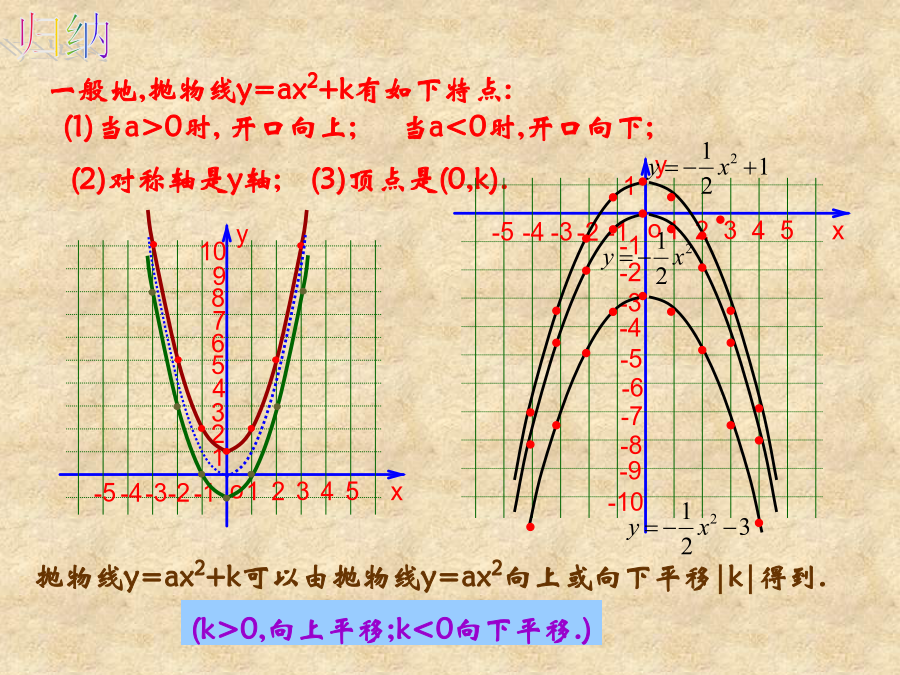
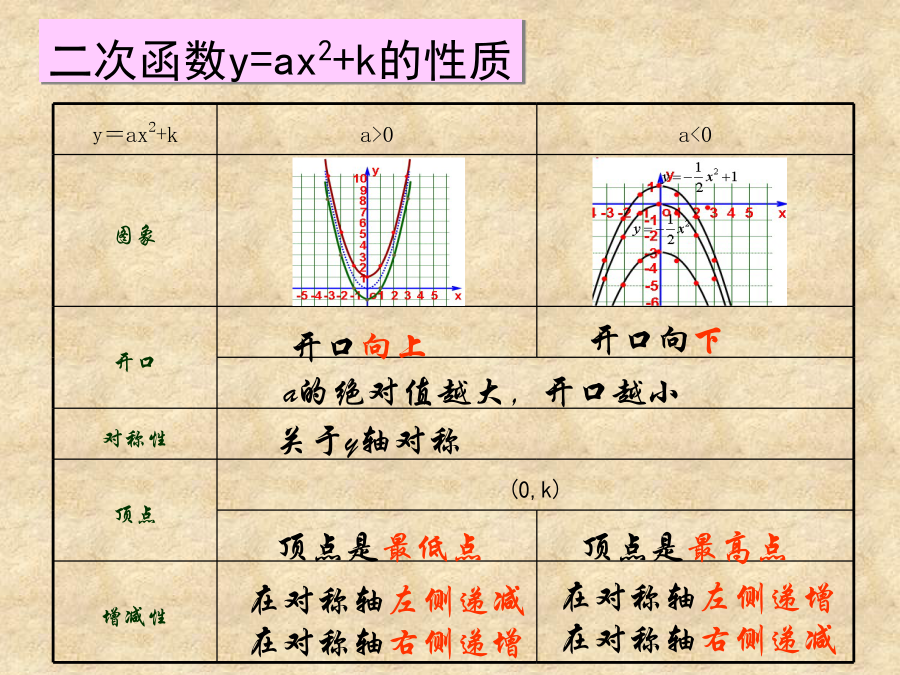
26.1二次函数y=ax2+k图象和性质回顾：二次函数的图像二次函数的图像归纳y＝ax2+k（1）抛物线y=−2x2+3的顶点坐标是,对称轴是，当X___时，y随着x的增大而增大；在___侧，y随着x的增大而减小，当x=___时，函数y的值最大，最大值是,它是由抛物线y=−2x2线向___平移___个单位得到.4、按下列要求求出二次函数的解析式：（1）已知抛物线y=ax2+c经过点（-3，2）（0，-1）,求该抛物线线的解析式。
2024-08-19
10
903KB
二次函数y=ax2+k的图像和性质.doc
课题：§22.1.3二次函数y=a(x-h)2+k的图像和性质主备人：何永红教学目标1.会用列表描点法画二次函数的图像.2.掌握二次函数y=ax2+k（a≠0）的基本性质.3.进一步渗透数形结合的数学思想，增强一定的问题探究、合作意识，培养细心观察、理性归纳的数学思维品质.教学重点二次函数图像的画法及其性质教法学法个人自学、小组交流、合作、探究教学准备活动单、课件活动方案导学策略个性调整【活动方案】活动一：探究y=ax2+k（a≠0）的图像和性质.1.运用列表描点法在同一直角坐标系中画二次函数y=x2，y
2024-11-01
8
1.5MB
二次函数y=ax^2+k的图像和性质.ppt
根据左边已画好的函数图象填空：（1）抛物线y=2x2的顶点坐标是,对称轴是，在侧，y随着x的增大而增大；在侧，y随着x的增大而减小，当x=时，函数y的值最小，最小值是,抛物线y=2x2在x轴的方（除顶点外）。有一条抛物线形状的隧道，隧道的最大高度为6m，跨度为8m，把它放在如图所示的平面直角坐标系中。（1）求这条抛物线所对应的函数关系式；（2）若要在隧道壁上点P处安装一盏照明灯，灯离地面高为4.5m，求灯与点B的距离。2021/5/6课堂小结练习：已知点（x1，y1），（x2，y2）均在抛物线y=x2－1
2024-01-17
11
1KB
22131二次函数y=ax2+k的图像和性质-.doc
昂思多初级中学九年级数学教案课题22.1.3.1二次函数y=ax2+k的图像和性质课时第三课时教学目标1、使学生能利用描点法正确作出函数y＝ax2＋b的图象。2、让学生经历二次函数y＝ax2＋bx＋c性质探究的过程，理解二次函数y＝ax2＋b的性质及它与函数y＝ax2的关系。重点：难点：会用描点法画出二次函数y＝ax2＋b的图象，理解二次函数y＝ax2＋b的性质，理解函数y＝ax2＋b与函数y＝ax2的相互关系是教学重点。[来源:Zxxk.Com]正确理解二次函数y＝ax2＋b的性质，理解抛物线y＝ax2
2024-06-06
10
81KB
22131二次函数y=ax2+k的图像和性质.doc
旦马乡初级中学教学方案授课题目22.1.3.1二次函数y=ax2+k的图像和性质授课班级九年级授课时间2016.授课教师武学鹏教学目标及教学过程教学目标知识与能力目标使学生能利用描点法正确作出函数y＝ax2＋b的图象。方法与情感目标让学生经历二次函数y＝ax2＋bx＋c性质探究的过程，理解二次函数y＝ax2＋b的性质及它与函数y＝ax2的关系。教学重点会用描点法画出二次函数y＝ax2＋b的图象，理解二次函数y＝ax2＋b的性质，理解函数y＝ax2＋b与函数y＝ax2的相互关系。[来教学难点正确理解二次函数
2024-06-05
10
131KB