量子理论--微观粒子的波粒二象性.ppt

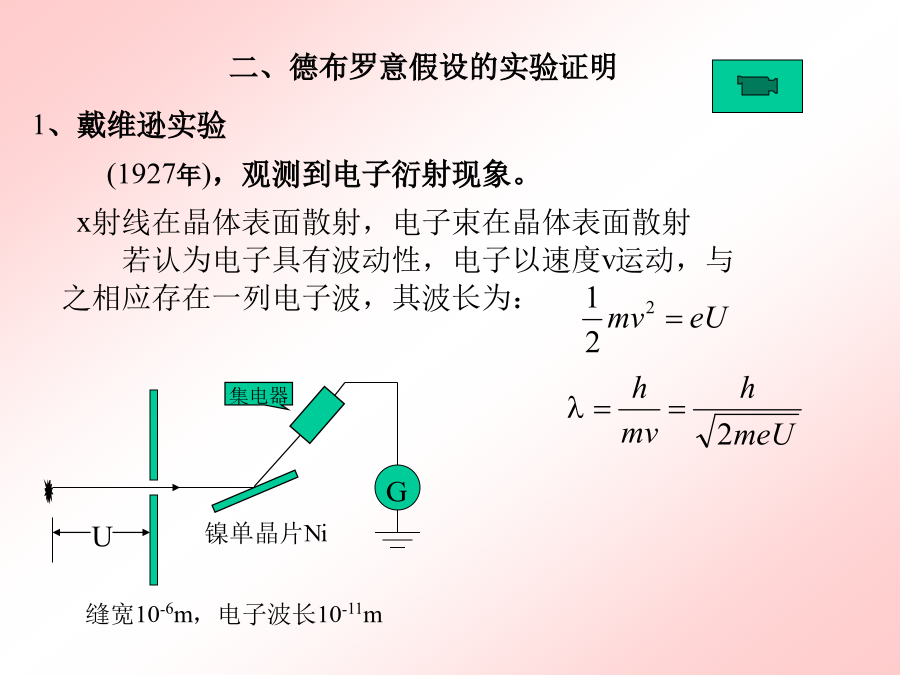
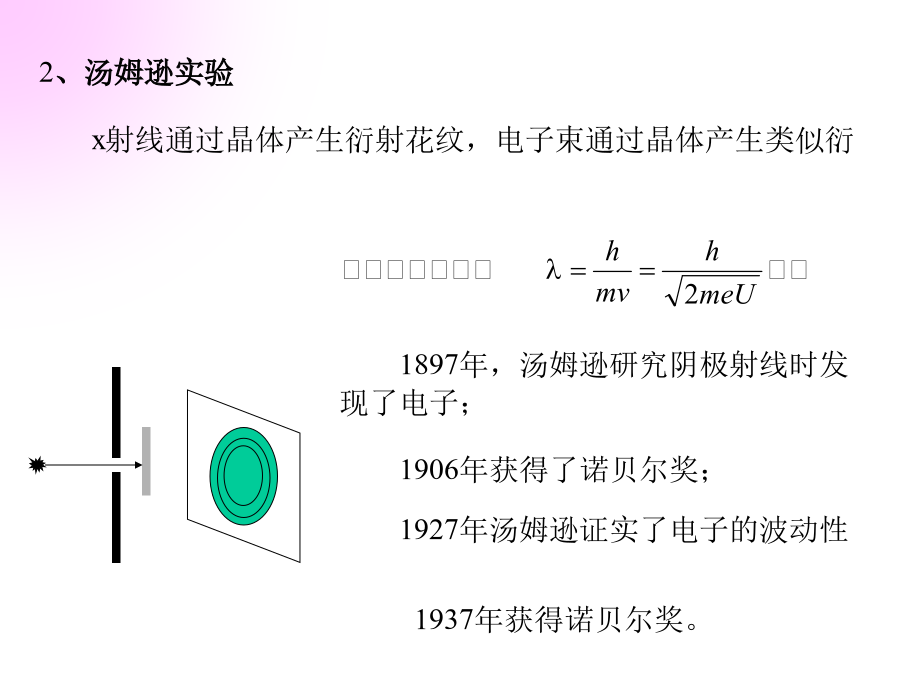
第五节1924年，德布罗意在光的波粒二象性的启发下，提出一个大胆的假设：波粒二象性不是光才具有，一切实物粒子(电子、质子、中子……)均具有波粒二象性。自然界的对称性的又一重大表现。德布罗意假设：不仅光具有波粒二象性，一切实物粒子如电子、原子、分子都具有波粒二象性。二、德布罗意假设的实验证明X射线2、汤姆逊实验电子的单缝、双缝、三缝和四缝衍射实验e德布罗意获1929年诺贝尔物理奖其它粒子波动性的实验证明
1930年，斯特恩作了分子波动性的实验
用氟化锂对H2和He分子散射时出现了极大值
我们引用斯特恩论文中一组实验数据来说明按麦氏分布最大能量概率正比于例：m=0.01kgv=300m/s的子弹1.单电子双缝实验
现代实验技术可以做到一次一个电子通过缝随着电子数目的增多
在屏上逐渐形成了衍射图样

说明“一个电子”就具有的波动性3)结论：
微观粒子在某些条件下表现出粒子性
在另一些条件下表现出波动性
两种性质虽寓于同一体中
却不能同时表现出来计算经过电势差U1=150V和U2=104V加速的电子的德布罗意波长（不考虑相对论效应）。四、德布罗意波与玻尔量子化假设五、不确定关系的表述和含义
海森堡（Heisenberg）在1927年提出微观粒子运动的基本规律
包含多种表达式其中两个是WernerKarlHeisenberg
德国人
1901-1976
创立量子力学六、不确定关系的简单导出若想得到单色光即要求严格的理论给出不确定性关系:三、能量与时间的不确定性关系例1.原子中电子运动不存在“轨道”
分析:即x=0.0001m电子的横向弥散可以忽略轨道有意义1)从量子过渡到经典的物理条件例3：判断电子不是原子核的基本成份
(电子不可能稳定在原子核内)
分析:
原子核线度这样的动量对应的电子能量有多大？例4估算一些物理量的量级
估算H原子的轨道半径r
H原子最稳定的半径--玻尔半径假设核静止按非相对论
电子能量为最稳定即能量最低例题波长=500nm的光波沿x轴正向传播，如果光波波长的不确定量(谱线宽度)=10-4nm，求光子位置、坐标的不确定量(xpxh)。例二、已知=500nm，光沿x轴传播，如果光波长的不准确度为已知/=10-7，求光子位置的不确定量x。例四写出实物粒子德布罗意波长与粒子动能Ek和静止质量m0的关系，并证明：例在电子单缝衍射实验中，若缝宽为a=0.1nm(1nm=10-3m)，电子束垂直射在单缝上，则衍射的电子横向动量的最小不确定量py=________N·s(普朗克常量h=6.6310-34J·s)(1)粒子的动量不可能确定。例题已知某电子的德布罗意波长和光子的波长相同试证：如果确定一个运动的粒子的位置时，其不确定量等于这粒子的德布罗意波长，则同时确定这粒子的速度时，其不确定量将等于这粒子的速度(测不准关系式x·pxh)。