方法确认等[1].ppt

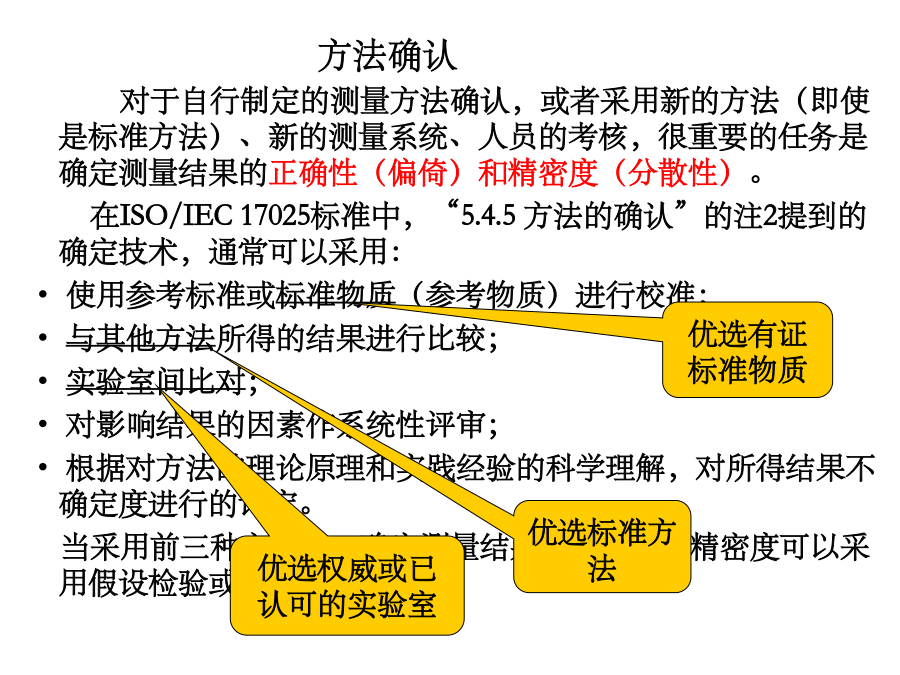
方法确认
对于自行制定的测量方法确认，或者采用新的方法（即使是标准方法）、新的测量系统、人员的考核，很重要的任务是确定测量结果的正确性（偏倚）和精密度（分散性）。
在ISO/IEC17025标准中，“5.4.5方法的确认”的注2提到的确定技术，通常可以采用：
使用参考标准或标准物质（参考物质）进行校准；
与其他方法所得的结果进行比较；
实验室间比对；
对影响结果的因素作系统性评审；
根据对方法的理论原理和实践经验的科学理解，对所得结果不确定度进行的评定。
当采用前三种方法时，确定测量结果的正确性和精密度可以采用假设检验或其他统计方法。1.系统偏差的检验
一般测量可采用正态检验和t检验。
当总体标准偏差σ已知（如规范规定了该测量的标准偏差或重复性限，或者通过以往大量实验资料统计得到最佳测量能力等。）时，可采用正态检验；
当总体标准偏差σ未知时，可采用t检验。
1)使用参考标准或标准物质（参考物质）进行确认
这是对新方法正确性（系统偏差）最可靠的确认，因为参考标准或标准物质的值，可看作相对真值。
当σ已知时，可采用正态检验。
对参考标准或标准物质进行n次重复测量，求得平均值。
作统计量：

、分别为参考标准或标准物质的已知值和标准偏差。通常显著水平取，若≤1.96，则新方法正确性可接受。
如果参考标准或标准物质的标准偏差可忽略，则上式不计，统计量变为：

当σ未知（通常是这样），可采用t检验。
对参考标准或标准物质进行n次重复测量，求得平均值和标准偏差S。作统计量：

显著水平如果取，则查表得到置信概率95%，自由度为的t分布临界值，若，则新方法正确性可接受。2)与其他方法所得的结果进行比较
由于其他方法所得的测量结果不一定是确定值，所以新方法的正确性仅仅是相对于其他方法的正确性而言，因此最好选择与标准方法所得的结果进行比较。
当σ已知时，可采用正态检验。
用两种方法分别对同一样品进行重复测量，设新方法标准偏差为，测量样品次，求得平均值；其他方法标准偏差
，测量样品次，求得平均值。作统计量：

通常显著水平取，若≤1.96，则新方法正确性与其他方法正确性一致。
当σ未知，可采用t检验。
用两种方法分别对同一样品进行重复测量，设新方法测量样品次，求得平均值和标准偏差；其他方法测量样品次，求得平均值和标准偏差。
作统计量：

显著水平如果取，则查表得到置信概率95%，自由度为的t分布临界值，若
，则新方法正确性与其他方法一致。
如果两种方法重复测量次数相同，统计量简化为：
（自由度仍为）
3)实验室间比对
一般两个实验室间比对所得的结论，也仅仅是两个实验室之间正确性的一致程度，因此最好参加实验室间比对计划，或优先选择权威实验室或已认可的实验室进行比对。
当σ已知时，可采用正态检验；当σ未知，可采用t检验。统计量及确认方法同上述《2)与其他方法所得的结果进行比较》。

2.标准差假设检验
通常可采用检验和F检验。
假设检验，可以判定重复多次测量的标准偏差S与规定的标准偏差σ（总体标准偏差已知）是否一致；
F假设检验，可以判定两个独立的重复多次测量标准偏差
与是否一致。
(1).检验
1).分布
若ν个随机变量均服从标准正态分布N（0，1），则其平方和是参数为ν的随机变量。
分布密度函数为:
ν=1
ν=2
x>0ν=6
数学期望为：
方差为：
标准差σ为：

2）.检验
检验是检验一组数据的标准差是否等于所规定的，即假设

的否定域的否定域

可取统计量

检验的否定域为:

检验的否定域为:(2).F检验
1).F分布
两独立分布随机变量除于各自自由度商的分布,分子、分母的随机变量的自由度，按次序为F分布随机变量的自由度。
分布密度函数为:

方差为：

标准差σ为：
(2）.F检验
F检验适合于两个正态总体方差是否一致的比较。
即:采用两种方法对同一样品进行检测，如果方差比的统计量服从F分布，则两种方法检验的测量列均服从正态分布。
取统计量

若显著水平取，当时，则两方差符合，即两种方法分散性一致。
若或，则两方差不符合。

由两种方法测量的自由度、和显著水平，查得
值，而值由下式得到。
例1.实验室对某标准物质中A成份进行7次测定，得：16.9、
14.3、17.6、16.5、15.5、17.0、15.9。有证标准物质给出的值为
，标准偏差。
试检验该实验室检测的（正确性和精密度）是否达到要求。
该实验室检测结果平均值为

标准偏差为

设显著性水平α=0.05，
该实验室总体标准差已知，检验正确性采用正态检验，统计量：

因为0.62<1.96，所以该实验室检测的正确性可以接受。为检验该实验室重复多次测量的标准偏差S与规定的标准偏差是否一致，可采用假设检验。
设显著性水平α=0.05，有统