
数学建模-最优化模型.ppt

kp****93









亲,该文档总共47页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

数学建模中的优化模型.ppt
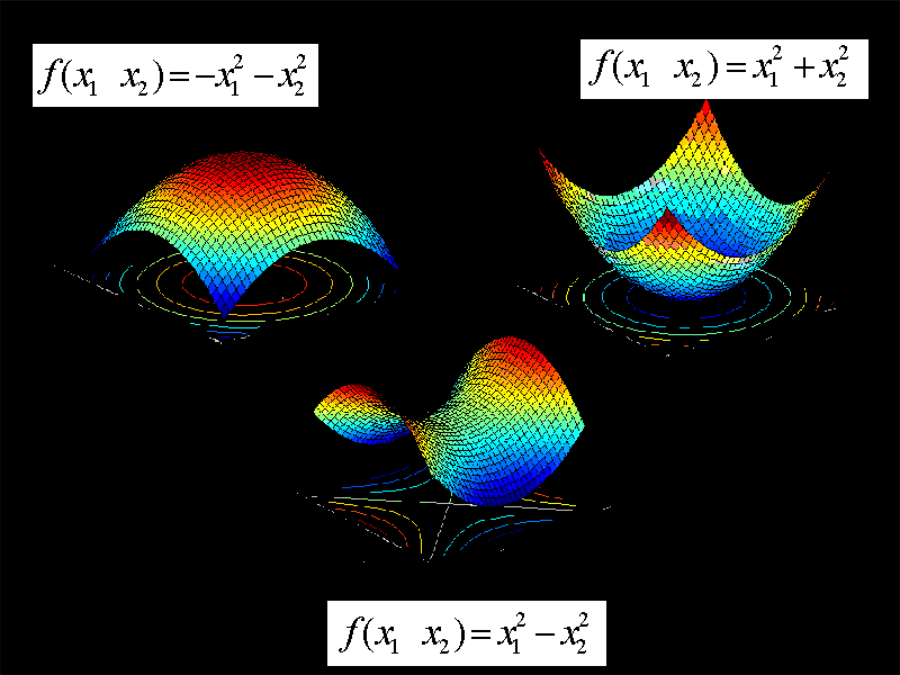
1.优化模型简介优化问题的一般形式无约束优化:最优解的分类和条件约束优化的简单分类优化建模如何创新?建模时需要注意的几个基本问题常用优化软件2.简单的优化模型——生猪的出售时机求t使Q(t)最大敏感性分析敏感性分析强健性分析3.数学规划模型如果生产某一类型汽车,则至少要生产80辆,那么最优的生产计划应作何改变?设每月生产小、中、大型汽车的数量分别为x1,x2,x3模型求解IP可用LINGO直接求解其中3个子模型应去掉,然后逐一求解,比较目标函数值,再加上整数约束,得最优解:LINGO中对0-1变量的限定:

数学建模培训_优化模型.ppt
..............
数学建模-最优化模型.ppt
最优化模型最优化方法概述在实际生活当中,人们做任何事情,不管是分析问题,还是进行决策,都要用一种标准衡量一下是否达到了最优。(比如基金人投资)在各种科学问题、工程问题、生产管理、社会经济问题中,人们总是希望在有限的资源条件下,用尽可能小的代价,获得最大的收获。(比如保险)数学家对最优化问题的研究已经有很多年的历史。以前解决最优化问题的数学方法只限于古典求导方法和变分法(求无约束极值问题),拉格朗日(Lagrange)乘数法解决等式约束下的条件极值问题。计算机技术的出现,使得数学家研究出了许多最优化方法和算

数学建模-最优化模型.ppt
最优化模型最优化方法概述在实际生活当中,人们做任何事情,不管是分析问题,还是进行决策,都要用一种标准衡量一下是否达到了最优。(比如基金人投资)在各种科学问题、工程问题、生产管理、社会经济问题中,人们总是希望在有限的资源条件下,用尽可能小的代价,获得最大的收获。(比如保险)数学家对最优化问题的研究已经有很多年的历史。以前解决最优化问题的数学方法只限于古典求导方法和变分法(求无约束极值问题),拉格朗日(Lagrange)乘数法解决等式约束下的条件极值问题。计算机技术的出现,使得数学家研究出了许多最优化方法和算

数学建模最优化模型.ppt
最优化方法的应用例:森林救火费用最小问题模型的假设易见表示单位时间内烧毁的森林面积当时,;设当时,得其最大值。设在中,为的线性函数,其斜率为;称为火势蔓延速度;在中,为的线性函数,其斜率为,其中为救火队员人数,为每个队员的平均灭火速度。每个救火队员单位时间的费用为,一次性支出的费用为,于是得到救火费用为不考虑森林地形分布的差异,同时也不考虑风向和风速的影响,并且一切救火设备和救火人员都正常工作。模型的建立和求解所以森林救火费用最小问题的数学模型为:上述问题是一个无约束的非线性规划问题,其最优解可用微分方法
