最大似然估计和贝叶斯参数估计.ppt

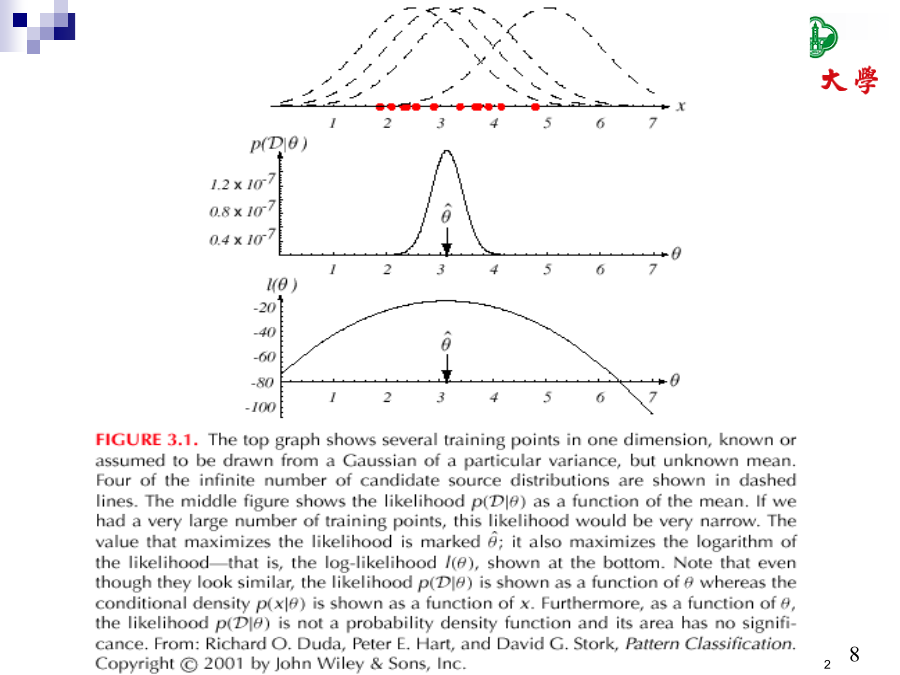
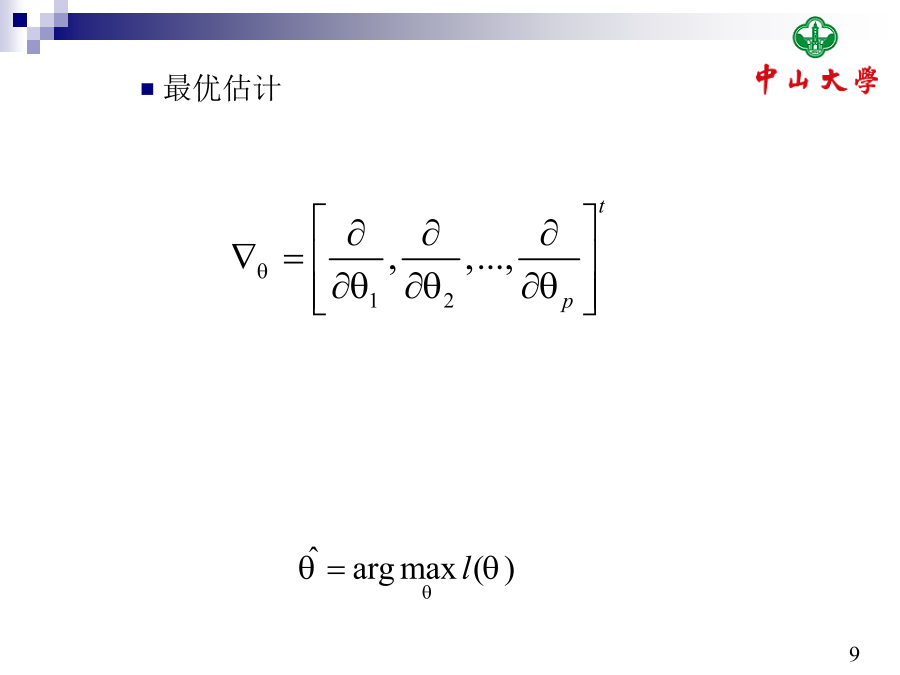
Chapter3:最大似然估计和贝叶斯参数估计要点：贝叶斯框架下的数据收集
在以下条件下我们可以设计一个可选择的分类器:
P(i)(先验)
P(x|i)(类条件密度)
不幸的是，我们极少能够完整的得到这些信息!

从一个传统的样本中设计一个分类器
先验估计不成问题
对类条件密度的估计存在两个问题：1）样本对于类条件估计太少了；2）特征空间维数太大了，计算复杂度太高。如果可以将类条件密度参数化，则可以显著降低难度。
例如：P(x|i)的正态性
P(x|i)~N(i,i)
用两个参数表示
将概率密度估计问题转化为参数估计问题。

估计
最大似然估计(ML)和贝叶斯估计；
结果通常很接近,但是方法本质是不同的。最大似然估计将参数看作是确定的量，只是其值是未知!通过最大化所观察的样本概率得到最优的参数—用分析方法。
贝叶斯方法把参数当成服从某种先验概率分布的随机变量，对样本进行观测的过程，就是把先验概率密度转化成为后验概率密度，使得对于每个新样本，后验概率密度函数在待估参数的真实值附近形成最大尖峰。

在这两种方法中，我们都用后验概率P(i|x)表示分类准则!
当样本数目增加时，收敛性质会更好；
比其他可选择的技术更加简单。

假设有c类样本，并且
1）每个样本集的样本都是独立同分布的随机变量；
2）P(x|j)形式已知但参数未知，例如P(x|j)~N(j,j)；
3）记P(x|j)P(x|j,j)，其中
使用训练样本提供的信息估计
=(1,2,…,c),每个i(i=1,2,…,c)只和每一类相关。

假定D包括n个样本,x1,x2,…,xn

的最大似然估计是通过定义最大化P(D|)的值
“值与实际观察中的训练样本最相符”
2最优估计
令=(1,2,…,p)t并令为梯度算子thegradientoperator

我们定义l()为对数似然函数：l()=lnP(D|)

新问题陈述:
求解为使对数似然最大的值

对数似然函数l()显然是依赖于样本集D,有：

最优求解条件如下:

P(xk|)~N(,)
(样本从一组多变量正态分布中提取)

这里=，因此:
的最大似然估计必须满足:

乘并且重新排序,我们得到:

即训练样本的算术平均值!

结论:
如果P(xk|j)(j=1,2,…,c)被假定为d维特征空间中的高斯分布;然后我们能够估计向量=(1,2,…,c)t从而得到最优分类!未知和，对于单样本xk =(1,2)=(,2)
对于全部样本，最后得到:

联合公式(1)和(2),得到如下结果:

2的最大似然估计是有偏的（渐进无偏估计）

的一个基本的无偏估计是:

模型错误会怎么样？在最大似然估计中被假定为固定值
在贝叶斯估计中是随机变量

目标:计算P(i|x,D)
假设样本为D，贝叶斯方程可以写成：因此，核心工作就是要估计假设的形式已知,参数的值未知，因此条件概率密度是知道的；
假设参数是随机变量，先验概率密度函数p()已知，利用贝叶斯公式可以计算后验概率密度函数p(|D)；
希望后验概率密度函数p(|D)在的真实值附件有非常显著的尖峰，则可以使用后验密度p(|D)估计；注意到单变量情形的p(|D)
复制密度结论:单变量情形的p(x|D)多变量情形:多变量学习3.5贝叶斯参数估计：一般理论问题:
p(x|D)是否能收敛到p(x)，计算复杂度如何？递归贝叶斯学习例1：递归贝叶斯学习例1：递归贝叶斯学习例1:Bayesvs.ML唯一性问题最大似然估计和贝叶斯参数估计的区别分类误差种类:Gibbs算法统计量
任何样本集D的函数；
充分统计量即是一个样本集D的函数s，其中s包含了有助于估计参数q的所有所有信息，即p(D|s,q)与q无关；
满足上面,如果q是随机变量，则可以写成因式分解定理：例子：多维高斯分布证明：必要性充分性：核密度（Kerneldensity）例子：多维高斯分布核密度与参数估计充分统计量与指数族函数分类问题通常涉及50或100维以上的特征.
分类精度取决于维数和训练样本的数量
考虑有相同协方差矩阵的两组多维向量情况:如果特征是独立的，则有:
最有用的特征是两类均值之间的距离大于标准方差的那些特征;
在实际观察中我们发现，当特征个数增加到某个临界点后会导致更糟糕的结果而不是好的结果:我们的模型有误，或者由于训练样本个数有限导致分布估计不精确，等等。
可分性与特征维数学习过程的计算复杂度分类过程的计算复杂度训练样本不足时的方法过拟合的概念缩并(RegularizedDiscriminantAnalysis