机械故障诊断—第三章信号分析.pptx

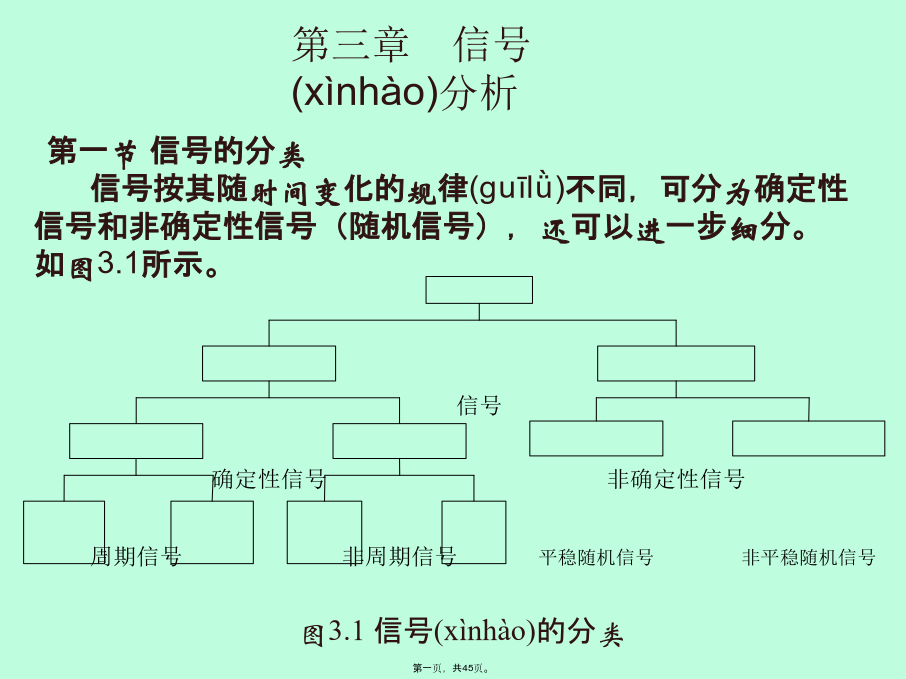
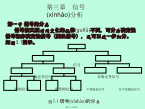
第三章信号(xìnhào)分析第二节信号(xìnhào)的预处理滤波的实质是去除或抑制(yìzhì)某些频率范围内信号成分。信号中有用成分s(t)与噪声n(t)的关系大体上有以下几种关系：
1相加关系x(t)＝s(t)+n(t)（3.2）
2相乘关系x(t)＝s(t)n(t)（3.3）
3卷积关系x(t)＝s(t)*n(t)（3.4）
第一种情况可用线性滤波的方法解决。但对于第二、三种情况，由于信号和噪声的叠加方式是非线性的，所以要使用非线性滤波方法来解决。1．线性滤波方法
就是能够从输入信号的全部频谱中分出一定频率范围的有用信号。为了获得良好的选择性，滤波器应以最小的衰减传输有用频段内的信号（称为通频带），而对其他(qítā)频段内的信号（称为阻频带）则给予最大的衰减。位于通频带与阻频带界线上的频率称为截止频率。
滤波器根据通频带可分为：
低通滤波器能传输0～f0频带内的信号；
高通滤波器能传输f0~∞频带内的信号；
带通滤波器能传输f1~f2频带内的信号；
带阻滤波器不能传输f1~f2频带内的信号。
阻频带内衰减特性的陡度与衰减数值越大滤波器的选择性越好。衰减特性如图3.2所示。衰减特性一般是以每倍频程衰减的分贝数来衡量的。如果SS(ω)和Sn(ω)的分布范围或分布特性不同，就有可能用这种基本的滤波方法将噪声分离或抑制，否则是不可能的，下面讨论两种情形：
①SS(ω)和Sn(ω)不重叠：这很容易用前述的某一种(yīzhǒnɡ)滤波器将它们分离。如图3.3（a）所示的情形，可用一截止频率为f0的低通滤波器（频率特性如虚线所示）将噪声去掉，但这种情况很少。
②SS(ω)和Sn(ω)部分重叠：如图3.3（b）所示的情形，如用合适的滤波器将非重叠部分的噪声去除，也能改善信噪比。2．其他类型的滤波方法
如果SS(ω)和Sn(ω)重叠，且统计分布特性不同，如当SS(ω)为若干个周期信号分量的谱，Sn(ω)为宽带随机噪声(zàoshēng)谱。周期分量在频谱上会呈现尖峰而易于辨认。但当噪声(zàoshēng)很强，宽带噪声(zàoshēng)谱起伏也很大时，如图3.4所示，就很难从噪声(zàoshēng)中辨认出周期分量来。出现这种情况则必须用其他滤波方法提取有用信号。（1）窄带滤波：如果周期分量的频率为ω0，用中心频率为ω0带宽为△ω的窄带滤波器对原始信号进行滤波。对周期分量，它的谱峰值在滤波后不随带宽而变化，但宽带随机噪声(zàoshēng)的能量是大致均布在一定频率范围内的，滤波后它的输出会随着带宽的减小而减小，因此窄带滤波器能有效地抑制这种噪声(zàoshēng)。
然而，如事先不知道周期分量的频率，则要不断改变带通滤波器的中心频率以检测出有用的周期分量，这种方法比较费事。
（2）相关滤波：因为周期性分量的自相关函数也是周期的，而宽带随机噪声(zàoshēng)的自相关函数在时延足够大时将衰减掉，如图3.5所示，所以利用自相关函数可以把噪声(zàoshēng)从周期信号中去掉。（3）时域平均滤波：这是从叠加有白噪声干扰的信号中提取周期性信号S（t）的一种很有效的方法。如果一信号x(t)由周期信号s(t)和白噪声n(t)组成，则
x(t)=s(t)+n(t)
我们(wǒmen)以s(t)的周期去截取信号x(t)，共截得N段，然后将各段对应点相加，由于白噪声的不相关性，可得到如图3.6所示的是截取不同的段数N，进行同步时域平均的结果。由图可见，虽然原来图形（N＝1）的信噪比很低，但经过(jīngguò)多段平均后，信噪比大大提高。当N＝256时，可以得到几乎接近理想的周期（正弦）信号，而原始信号中的周期分量，几乎完全被其他信号和随机噪声所淹没。3．同态滤波方法简介
如前所述，对于有用信号s(t)与噪声n(t)之间关系为相乘与卷积时，用线性滤波方法无法将它们分离，要用同态滤波方法。这里对此只作简单介绍。这种方法的特点是先将相乘或卷积混杂在一起的信号用某种变换将它们变成相加关系，然后用线性方法去掉不需要的成分，最后用前述变换的逆变换把滤波后的信号恢复出来。
（1）解乘积的同态滤波方法
实际中往往会遇到两个或多个分量相乘的信号。例如调幅信号可表示(biǎoshì)为载波信号和调制信号（包络信号）的乘积。
一般地，对于乘积形式的信号x(t)＝s(t)n(t)，可以用对数变换将相乘变为相加关系，即logx(t)=logs(t)+logn(t)，如果logs(t)和logn(t)的频谱都没有严重的重叠（如对调幅信号，调制信号频率和载波信号频率相差较多），就可以用线性滤波方法将它们分离开来，然后对滤波后分离出来的logs(t)作对数变换的逆变换－指数变换就可得到。（2）解卷积的同态滤波方法
在有多径反射和混响环境下作声强分析，会出现干扰与所需信号