
地震波运动学第六节——折射波运动学1.ppt

kp****93






亲,该文档总共50页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

地震波运动学第六节——折射波运动学1.ppt
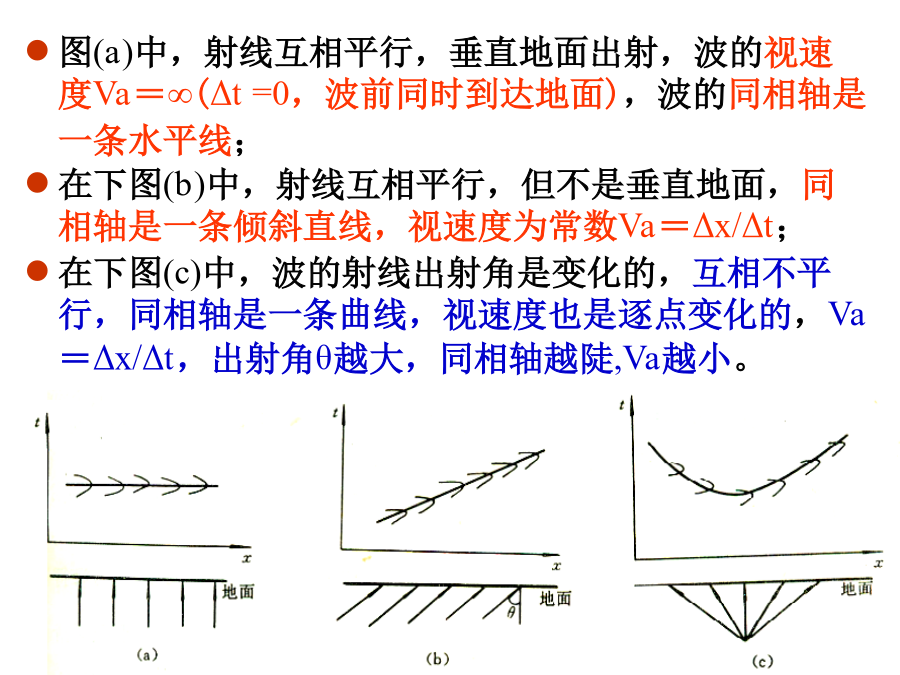
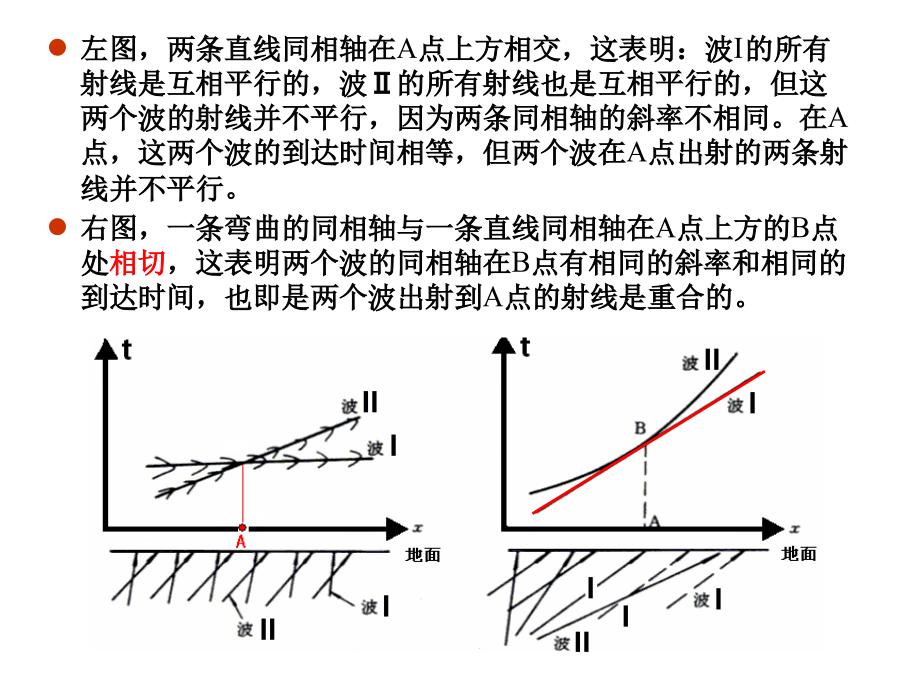
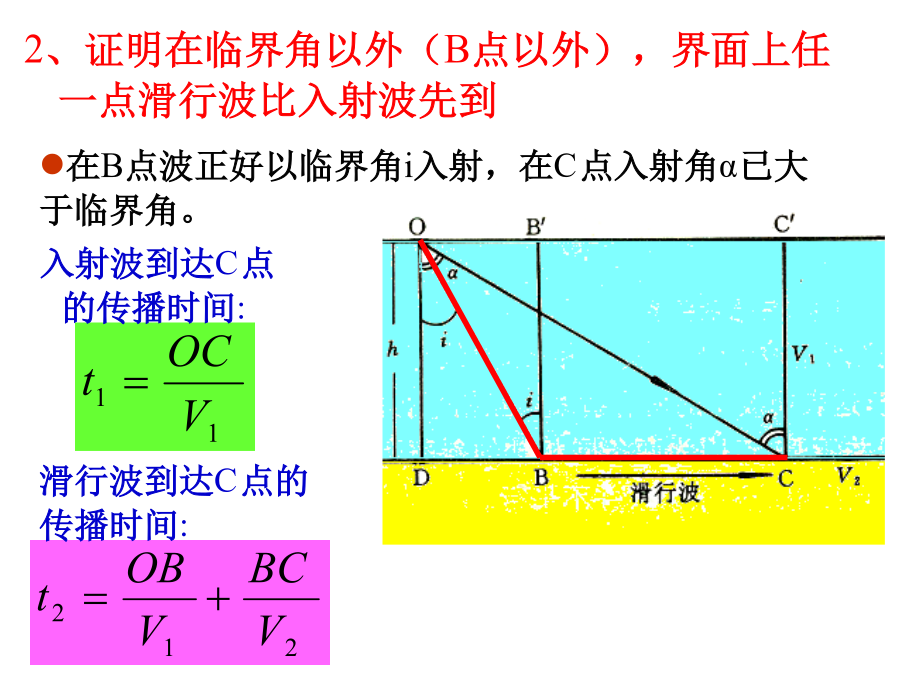
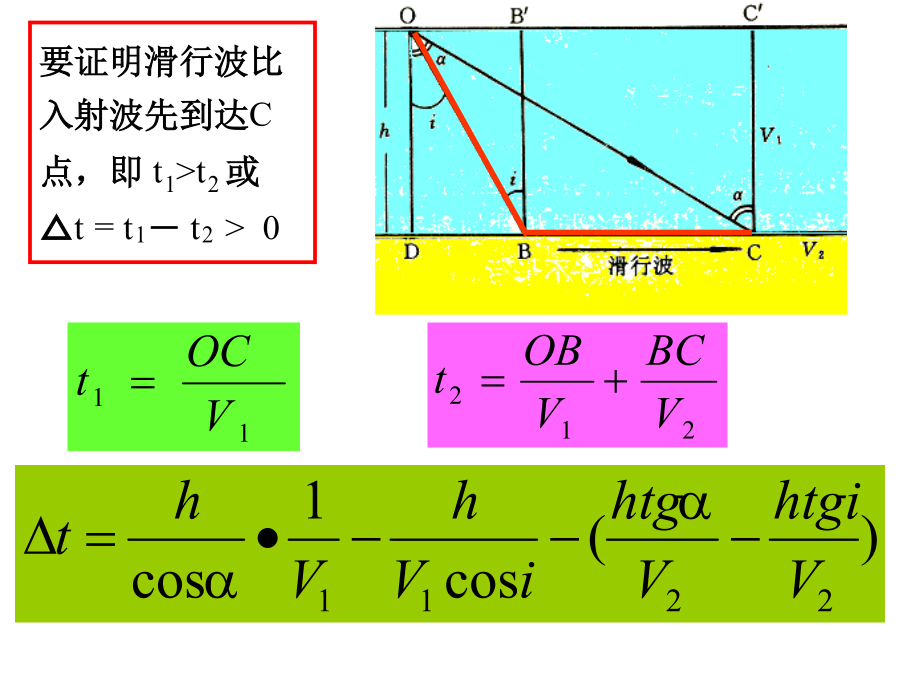
第一章主要内容一、视速度概念对折射波时距曲线的讨论,主要是关于如何用视速度概念来说明地震波传播的某些特点,即波出射到地面的射线的角度、地震剖面上同相轴的形态、波的视速度三者之间的关系。图(a)中,射线互相平行,垂直地面出射,波的视速度Va=∞(Δt=0,波前同时到达地面),波的同相轴是一条水平线;在下图(b)中,射线互相平行,但不是垂直地面,同相轴是一条倾斜直线,视速度为常数Va=Δx/Δt;在下图(c)中,波的射线出射角是变化的,互相不平行,同相轴是一条曲线,视速度也是逐点变化的,Va=Δx/Δt,出射

地震波运动学第六节——折射波运动学1 (2).ppt
第一章主要内容一、视速度概念对折射波时距曲线的讨论,主要是关于如何用视速度概念来说明地震波传播的某些特点,即波出射到地面的射线的角度、地震剖面上同相轴的形态、波的视速度三者之间的关系。图(a)中,射线互相平行,垂直地面出射,波的视速度Va=∞(Δt=0,波前同时到达地面),波的同相轴是一条水平线;在下图(b)中,射线互相平行,但不是垂直地面,同相轴是一条倾斜直线,视速度为常数Va=Δx/Δt;在下图(c)中,波的射线出射角是变化的,互相不平行,同相轴是一条曲线,视速度也是逐点变化的,Va=Δx/Δt,出射

地震波运动学a.ppt
地震波运动学(几何地震学)主要内容主要内容主要内容地震记录中的接收方式地震记录的几种接收(记录)方式单道记录与多道记录观测系统(测线参数)时距关系(曲线)地震记录中波至、相位和同相轴时距关系(曲线)讨论时距曲线的实际意义直达波的时距曲线水平反射界面的时距曲线2、共反射点反射水平层反射波时距曲线时距曲线tX2-T2曲线正常时差(NMO)正常时差正常时差正常时差定义正常时差的定量计算正常时差的定量计算动校正倾斜界面的反射时距曲线1、虚震源法2、共炮点反射波的时距曲线特征对倾斜界面反射波的时距曲线作变换:(2)
地震波的运动学资料.ppt
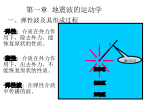
第一章地震波的运动学二、波的特征:二、波的特征:二、波的特征:4、振动图和波剖面(振动曲线和波动曲线):振动曲线:某质点在不同时刻的位置关系波动曲线:在某一时刻不同质点的位置关系二、波的特征:二、波的特征:三、地震波传播规律广义斯奈尔定律:假定:第i层纵波速度为:第i层横波速度为:第i层横波入射角:第i层横波透射角:射线参数:P2、费马(Fermat)原理:波在介质中的传播时,沿着时间最短路径传播。3、惠更斯(Huygens)原理:波在介质中传播所到达的各点,都可以看作新的波源。四、与地震有关的各种地震波

地震波运动学理论.docx
地震波运动学理论一、名词解释1.地震波运动学:研究在地震波传播过程中的地震波波前的空间位置与其传播时间的关系,即研究波的传播规律,以及这种时空关系与地下地质构造的关系。2.地震波动力学:研究地震波在传播过程中波形、振幅、频率、相位等特征的及其变化规律,以及这些变化规律与地下的地层结构,岩石性质及流体性质之间存在的联系。3.地震波:是一种在岩层中传播的,频率较低(与天然地震的频率相近)的波,弹性波在岩层中传播的一种通俗说法。地震波由一个震源激发。4.地震子波:爆炸产生的是一个延续时间很短的尖脉冲,这一尖脉冲
