
教育课件完美版高考数学大二轮复习精品文理通用课件:第1部分 专题2 函数与导数 第4讲.ppt

和蔼****娘子









亲,该文档总共66页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

教育课件完美版高考数学大二轮复习精品文理通用课件:第1部分 专题2 函数与导数 第4讲.ppt
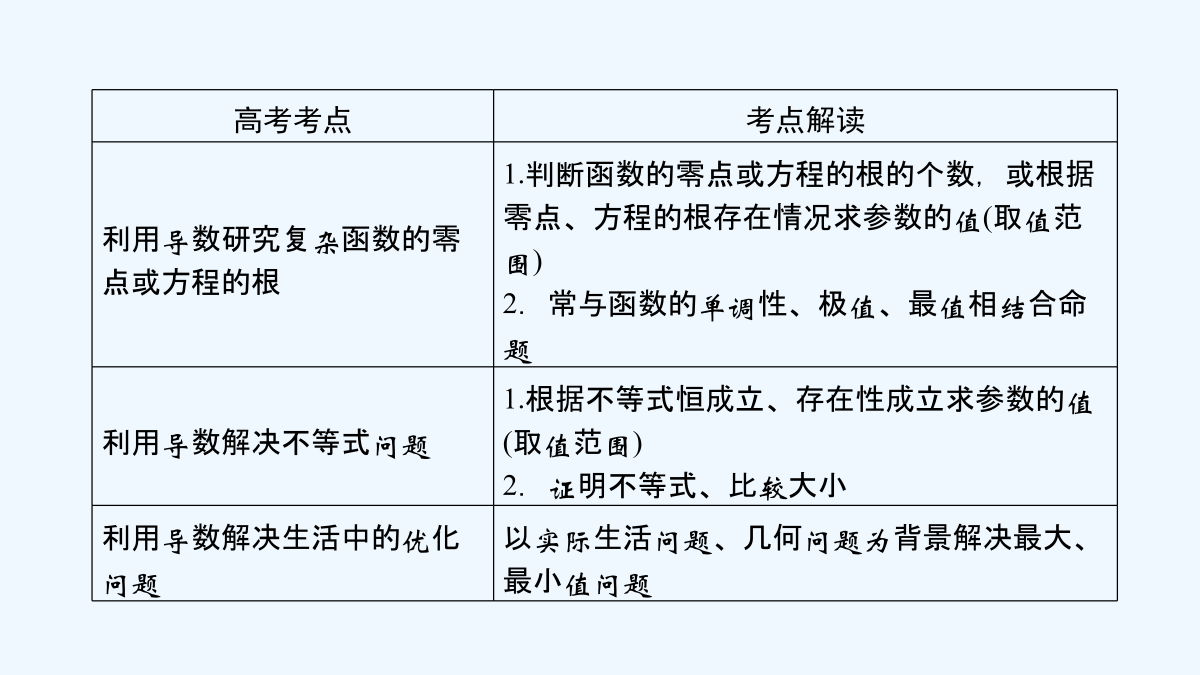
第一部分第四讲导数的综合应用1高考考点聚焦高考考点备考策略本部分内容在备考时应注意以下几个方面:(1)理解并掌握函数的零点的概念,求导公式和求导法则及不等式的性质.(2)熟练掌握利用导数研究函数零点,方程解的个数问题,及研究不等式成立问题、证明问题及大小比较的方法和规律.预测2019年命题热点为:(1)较复杂函数的零点,方程解的个数的确定与应用.(2)利用导数解决含参数的不等式成立及不等式证明问题.(3)利用导数解决实际生活及工程中的最优化问题.核心知识整合最大值最大值3.证明不等式问题不等式的证明可转化

教育课件完美版高考数学大二轮复习精品文理通用课件:第1部分 专题4 数列 第2讲.ppt
第一部分第二讲数列求和及综合应用1高考考点聚焦高考考点备考策略本部分内容在备考时应注意以下几个方面:(1)加强对递推数列概念及解析式的理解,掌握递推数列给出数列的方法.(2)掌握等差(比)数列求和公式及方法.(3)掌握数列分组求和、裂项相消求和、错位相减求和的方法.(4)掌握与数列求和有关的综合问题的求解方法及解题策略.预测2019年命题热点为:(1)已知等差(比)数列的某些项的值或其前几项的和,求该数列的通项公式.(2)已知某数列的递推式或某项的值,求该数列的和.(3)已知某个不等式成立,求某参数的值.

教育课件完美版高考数学大二轮复习精品文理通用课件:第1部分 专题4 数列 第1讲.ppt
第一部分知识网络构建第一讲等差数列、等比数列1高考考点聚焦高考考点备考策略本部分内容在备考时应注意以下几个方面:(1)加强对等差(比)数列概念的理解,掌握等差(比)数列的判定与证明方法.(2)掌握等差(比)数列的通项公式、前n项和公式,并会应用.(3)掌握等差(比)数列的简单性质并会应用.预测2019年命题热点为:(1)在解答题中,涉及等差、等比数列有关量的计算、求解.(2)已知数列满足的关系式,判定或证明该数列为等差(比)数列.(3)给出等差(比)数列某些项或项与项之间的关系或某些项的和,求某一项或某些

教育课件完美版高考数学大二轮复习精品文理通用课件:第1部分 专题8 选修系列 第2讲.ppt
第一部分第二讲不等式选讲1高考考点聚焦高考考点备考策略本部分内容在备考时应注意以下几个方面:不等式选讲也是高考必考内容,重点考查绝对值不等式的解法、不等式的证明及求参数取值范围问题.题型多为解答题,难度为中档.核心知识整合≤几何意义1.应用绝对值不等式性质求函数的最值时,一定要注意等号成立的条件.特别是多次使用不等式时,必须使等号同时成立.2.利用基本不等式证明要注意“一正、二定、三相等”三个条件同时成立,缺一不可.3.在去掉绝对值符号进行分类时要做到不重不漏.高考真题体验命题热点突破命题方向1绝对值不等

教育课件完美版高考数学大二轮复习精品文理通用课件:第1部分 专题8 选修系列 第1讲.ppt
第一部分第一讲坐标系与参数方程1高考考点聚焦高考考点备考策略本部分内容在备考时应注意以下知识点:一是参数方程、极坐标与曲线的关系;二是由参数方程、极坐标方程求解曲线的一些基本量,主要是极坐标与直角坐标、参数方程(直线、圆、椭圆的参数方程)与普通方程的互化问题的应用等,考查知识点较为简单和稳定,这也为大家的备考指明了方向.核心知识整合1.极坐标与直角坐标互化的前提是把直角坐标系的原点作为极点,x轴正半轴作为极轴,且在两坐标系中取相同的长度单位.2.在将曲线的参数方程化为普通方程时,不仅仅是要把其中的参数消去
