
耦合光电振荡器的解耦分析方法.pdf

小沛****文章








在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

耦合光电振荡器的解耦分析方法.pdf
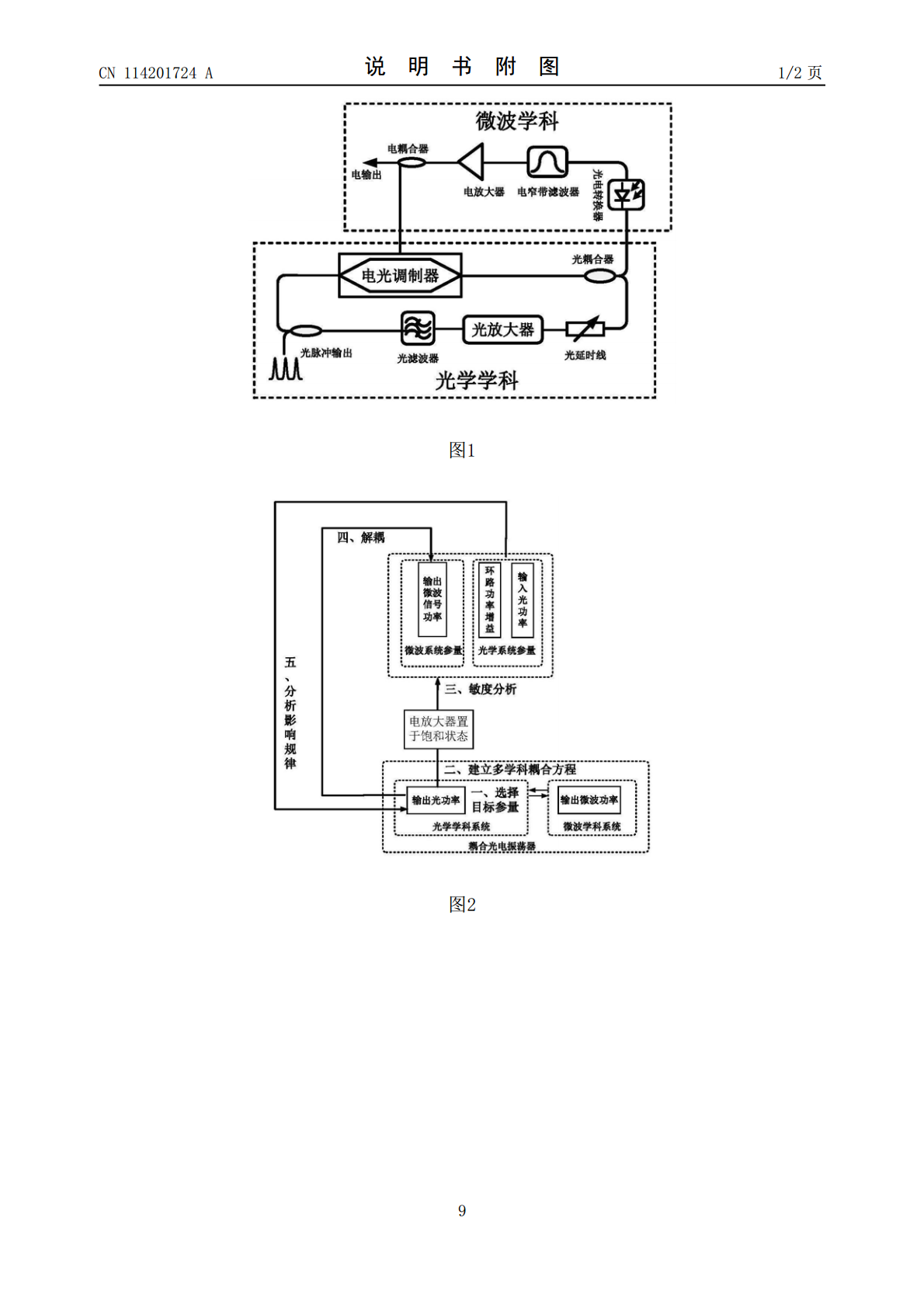
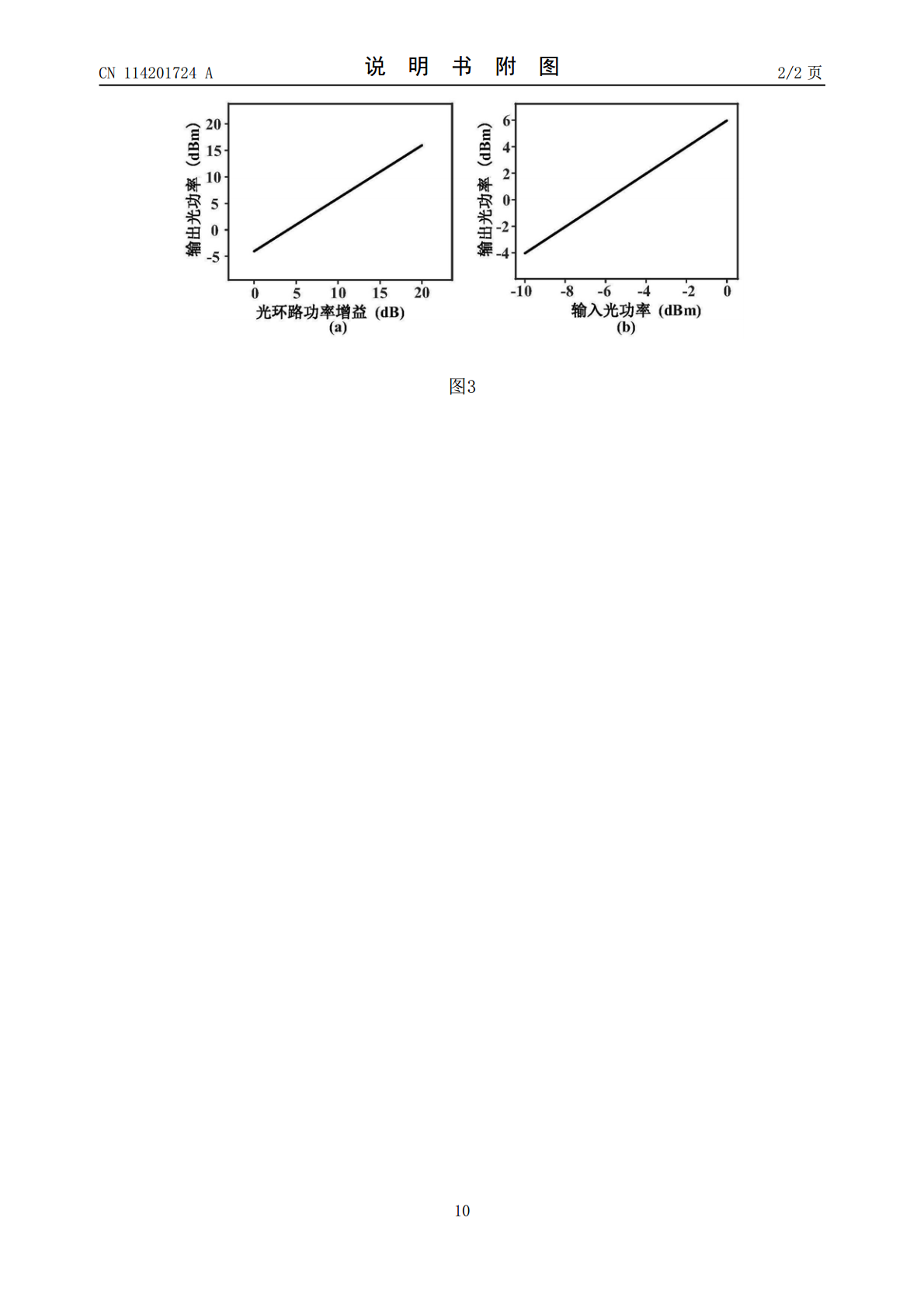
本发明公开了一种耦合光电振荡器的解耦分析方法,包括以下步骤:依据所要解耦合的目标参量,确定相应的耦合变量及设计变量,并建立多学科耦合方程;在耦合变量中的一个趋于稳定不再发生变化的状态下,基于所述多学科耦合方程直接求另一个耦合变量对于各设计变量的导数,从而获得目标参量对于各个设计变量的敏度信息;依据所得到的敏度信息,将多学科耦合方程中目标参量的不敏感设计变量替换为常量,即得到目标参量的解耦合方程;基于解耦合方程,分析其中的敏感设计变量对于目标参量的影响规律。相比现有技术,本发明基于耦合光电振荡器自身的固有特

机械耦合系统的解耦方法.docx
机械耦合系统的解耦方法机械耦合系统解耦方法摘要:机械耦合系统是由多个相互联系的机械组件组成的系统。在实际应用中,为了满足不同的要求,往往需要对机械耦合系统进行解耦。本论文介绍了机械耦合系统的解耦方法,包括主动解耦、被动解耦和混合解耦方法,并针对每种方法进行了分析和评价。1.引言机械耦合系统广泛应用于各种工业和科学领域。然而,由于机械组件之间的相互影响,机械耦合系统的性能往往会受到限制。为了解决这个问题,需要对机械耦合系统进行解耦,以便提高系统的性能和可靠性。本论文将介绍机械耦合系统的解耦方法,并对每种方法

倾斜转弯导弹控制耦合分析与解耦方法研究.docx
倾斜转弯导弹控制耦合分析与解耦方法研究随着现代导弹技术的不断发展,倾斜转弯导弹逐渐成为了导弹领域的一种新型导弹。倾斜转弯导弹拥有高速度、高机动性和低探测性等优点。当导弹进行高速度、高机动性的倾斜转弯操作时,由于气动力和控制力之间的高度相互耦合,在相应的导弹控制过程中会产生“控制耦合”现象,导致导弹失控或者不能达到预期的控制效果。因此,为了更好的掌控倾斜转弯导弹,在导弹开发的过程中,需要对倾斜转弯导弹控制耦合进行分析和解耦。本文主要介绍了导弹控制耦合的形成原因,以及相关的分析和解耦方法。首先,导弹控制耦合的

针对绳索运动耦合的被动解耦机构及其解耦方法.pdf
本发明公开了一种针对绳索运动耦合的被动解耦机构及其解耦方法,尤其涉及多关节的绳驱动串联机械臂系统。该机构包括固定轮、随动轮、主动轮、导向滑轮、解耦绳索。主动轮与关节连杆连接,固定轮与关节基座连接,利用解耦绳索的正反向缠绕驱动随动轮,实现随动轮运动速度是关节连杆旋转速度的1/2。后端关节的驱动绳索按随动轮上的导线槽正反向缠绕,这样,由关节连杆转动引起的驱动绳索位移变化和由随动轮转动导致的位移变化相互抵消。经过解耦机构后的驱动绳索与关节连杆无相对位移,实现绳索的运动解耦。该解耦机构可以工作在0~300℃范围内

全解耦硅MEMS陀螺仪正交耦合分析.docx
全解耦硅MEMS陀螺仪正交耦合分析全解耦硅MEMS陀螺仪正交耦合分析摘要:硅微电子机械系统(MEMS)技术的发展已经使得MEMS陀螺仪成为一种重要的姿态和导航传感器。然而,MEMS陀螺仪中的正交耦合效应对其精度和性能具有严重的影响。为了有效地解决这个问题,本文通过深入分析和研究MEMS陀螺仪的正交耦合效应,提出了全解耦的解决方案。该方案将MEMS陀螺仪的结构和工作原理进行了改进,减小了正交耦合效应,并极大地提升了陀螺仪的精度和性能。1.引言MEMS陀螺仪作为一种重要的惯性传感器,在航空航天、导航和姿态控制
