2023年新疆乌鲁木齐市中考数学一模试卷(原版版).pdf

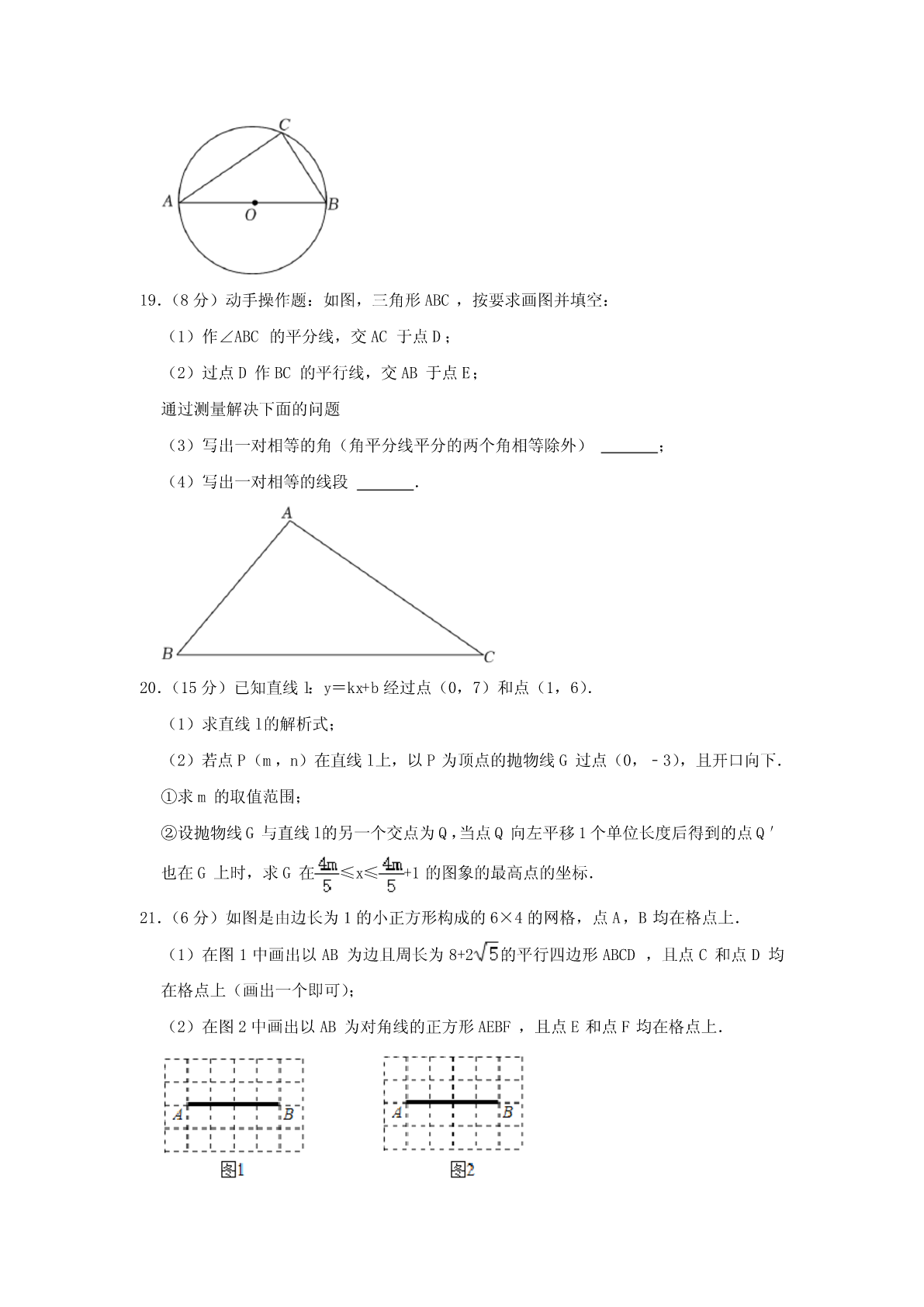
2023年新疆乌鲁木齐市中考数学一模试卷

一、选择题（共10小题，每小题5分，共50分）每题的选项中只有一项符合题目要求.

1．（5分）﹣2023的绝对值是（）

A．﹣B．﹣2023C．D．2023

2．（5分）下列命题中，假命题是（）

A．对顶角相等

B．同一平面内，过一点有且只有一条直线与已知直线垂直

C．同一平面内，过直线外一点有且只有一条直线与这条直线平行

D．如果a＞c，b＞c，那么a＞b

3．（5分）如果将抛物线y＝5x2向上平移1个单位，那么所得新抛物线的表达式是（）

A．y＝5（x+1）2B．y＝5（x﹣1）2C．y＝5x2+1D．y＝5x2﹣1

4．（5分）如图，小颖按下面方法用尺规作角平分线：在已知的∠AOB的两边上，分别截取

OC，OD，使OC＝OD．再分别以点C，D为圆心、大于的长为半径作弧，两弧在

∠AOB内交于点P，作射线OP，则射线OP就是∠AOB的平分线．其作图原理是：△

OCP≌△ODP，这样就有∠AOP＝∠BOP，那么判定这两个三角形全等的依据是（）

A．SASB．ASAC．AASD．SSS

5．（5分）如图，已知Rt△ABC中，∠C＝90°，tanA＝．D、E分别是边BC、AB上的

点，DE∥AC，且BD＝2CD．如果⊙E经过点A，且与⊙D外切，那么⊙D与直线AC的

位置关系是（）

A．相离B．相切C．相交D．不能确定
6．（5分）已知在Rt△ABC中，∠C＝90°，cotA＝，那么以边AC长的倍为半径的圆A

与以BC为直径的圆的位置关系是（）

A．外切B．相交C．内切D．内含

7．（5分）如果将抛物线y＝（x+1）2﹣1向上平移2个单位，那么平移后抛物线的顶点坐

标是（）

A．（0，2）B．（2，0）C．（1，1）D．（﹣1，1）

8．（5分）在Rt△ABC中，∠C＝90°，BC＝8，tanA＝2，以点A为圆心，半径为8的圆记

作圆A，那么下列说法正确的是（）

A．点C在圆A内，点B在圆A外

B．点C在圆A上，点B在圆A外

C．点C、B都在圆A内

D．点C、B都在圆A外

9．（5分）将抛物线y＝2x2向右平移1个单位，再向上平移2个单位后，所得新抛物线和原

抛物线相比，不变的是（）

A．对称轴B．开口方向

C．和y轴的交点D．顶点

10．（5分）如图，已知点D、E、F、G、H、I分别在△ABC的三边上，如果六边形DEFGHI

是正六边形，下列结论中不正确的是（）

A．∠A＝60°

B．

C．＝

D．＝

二、填空题（共5小题，每小题2分，共10分）请把答案填在答卷中的相应位置处.
11．（2分）抛物线y＝﹣x2+2x﹣7与y轴的交点坐标为．

12．（2分）如图，在△ABC中，∠A＝30°，∠B＝90°，D为AB中点，E在线段AC上，

＝，则＝．

13．（2分）如图，△ABC中，AC＝3，BC＝4，AB＝5．四边形ABEF是正方形，点D是直

线BC上一点，且CD＝1．P是线段DE上一点，且PD＝DE．过点P作直线l与BC

平行，分别交AB，AD于点G，H，则GH的长是．

14．（2分）如图，正方形ABCD的边长为4，点E是边BC上一点，且BE＝3，以点A为

圆心，3为半径的圆分别交AB、AD于点F、G，DF与AE交于点H．并与⊙A交于点K，

连结HG、CH．给出下列四个结论．其中正确的结论有（填写所有正确结论的

序号）．

（1）H是FK的中点

（2）△HGD≌△HEC

（3）S：S＝9：16
△AHG△DHC
（4）DK＝

15．（2分）正方形ABCD中，AB＝2，点M是BC的中点，点P是正方形内一点，连接

PC，PM，当点P移动时，始终保持∠MPC＝45°，连接BP，点E，F分别是AB，BP

中点，求3BP+2EF的最小值为．

三、解答题（一）（本大题共1小题，满分15分）

16．（15分）计算：

（1）；

（2）（）﹣1+﹣4sin60°；

（3）+（3.14﹣π）0﹣3tan60°+|1﹣|+（﹣）﹣2．

四、解答题（二）（本大题共7小题，满分75分）

17．（9分）如图，直线l与a、b相交于点A、B，且a∥b．

（1）尺规作图：过点B作∠ABC的角平分线交直线a于点D（保留作图痕迹，标注有关

字母，不用写作法和证明）；

（2）若∠1＝48°，求∠ADB的度数；

（3）P为直线l上任意一点，若点D到直线b的距离为3cm，则DP的最小值为cm．

18．（16分）如图，AB是⊙O的直径，点C在⊙O上，且AC＝8，BC＝6．

（1）尺规作图：过点O作AC的垂线，交劣弧于点D，连接CD（保留作图痕迹，不

写作法）；