
大学物理电磁学总结.pdf

qw****27



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

大学物理电磁学总结.pdf
大学物理电磁学总结电磁学部分总结静电场部分第一部分:静电场的基本性质和规律电场是物质的一种存在形态,它同实物一样也具有能量、动量、质量等属性。静电场的物质特性的外在表现是:(1)电场对位于其中的任何带电体都有电场力的作用(2)带电体在电场中运动,电场力要作功——电场具有能量1、描述静电场性质的基本物理量是场强和电势,掌握定义及二者间的关系。电场强度E=q0∞Wa电势Ua==E⋅drq0a2、反映静电场基本性质的两条定理是高斯定理和环路定理Φe=E⋅dS=ε0∑qLE⋅dr=0要掌握各个定理的内容,所揭示的

大学物理电磁学总结.ppt
14、电流强度、电流密度、电流的连续性方程、稳恒电流;15、电动势。16、磁场、磁感应强度;17、磁通量;18、磁场中的高斯定理;19、毕奥-萨伐尔定律。20、毕奥-萨伐尔定律的应用;21、安培环路定理及其应用。22、磁场对载流导线和载流线圈的作用;23、安培定律;磁力的功。24、法拉弟电磁感应定律;25、楞次定律。26、动生电动势;27、感生电动势。28、自感应、互感应;29、自感磁能、磁场能量;30、位移电流、全电流定律、麦克斯韦方程组(积分形式)。一、库仑定律几种典型带电体的电场分布:3)无限大带电
大学物理电磁学总结.pdf
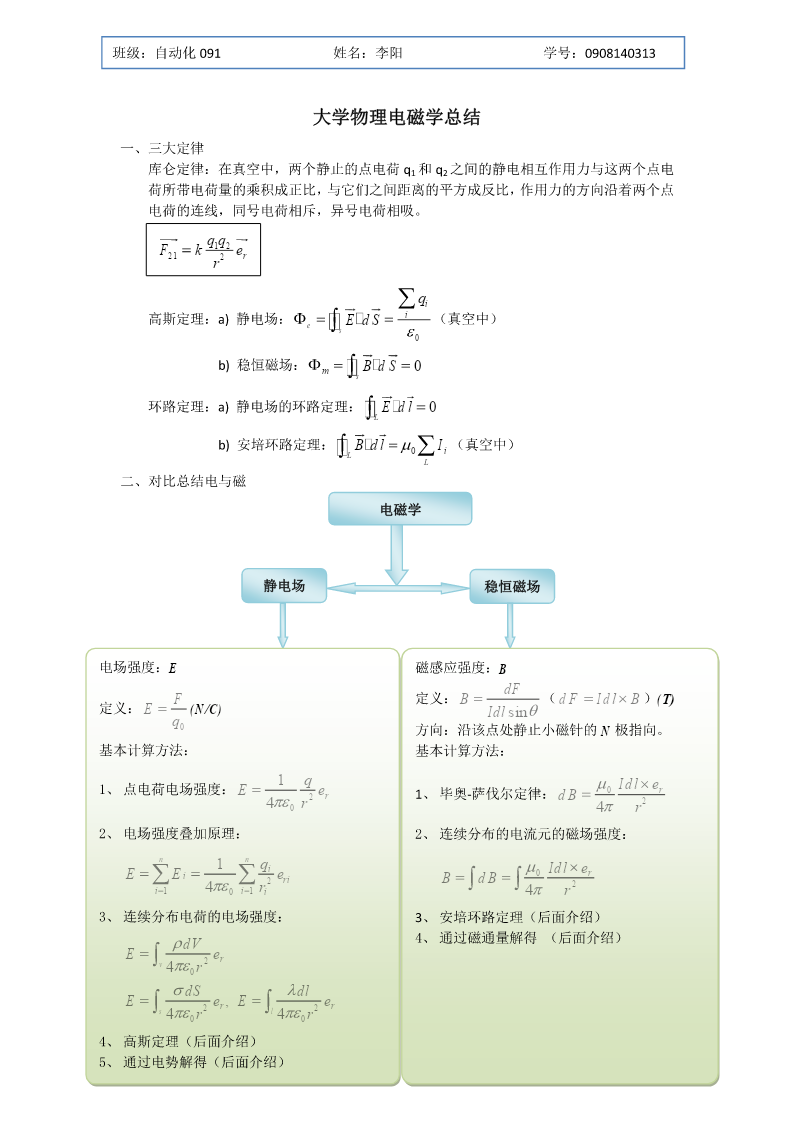
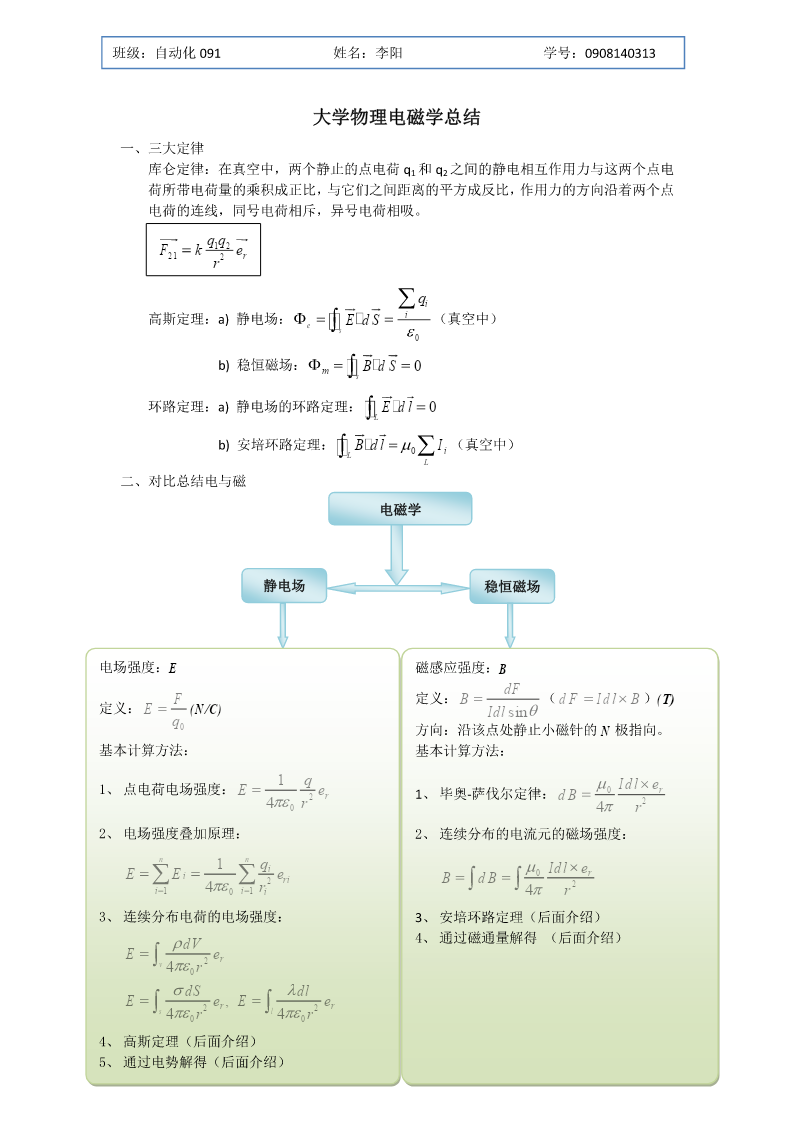
班级:自动化091姓名:李阳学号:0908140313大学物理电磁学总结一、三大定律库仑定律:在真空中,两个静止的点电荷q1和q2之间的静电相互作用力与这两个点电荷所带电荷量的乘积成正比,与它们之间距离的平方成反比,作用力的方向沿着两个点电荷的连线,同号电荷相斥,异号电荷相吸。qq12Fke21r2rqi高斯定理:a)静电场:EdSi(真空中)es0b)稳恒磁场:BdS0ms环路定理:a)静电场的环路定理:Edl0Lb)安培环路定理:BdlI(真空中)L0iL二、对比总结

大学物理电磁学总结大学物理与中学物理电磁学的衔接论文.pdf
大学物理电磁学总结|大学物理与中学物理电磁学的衔接论文作为高等院校理工农科等专业必修的一门基础理论课,大学物理对非物理类专业学生后续课程的学习和分析解决问题能力的提高都有很大帮助。通过中学物理的学习,大部分学生对大学物理课程中所要学习的一些物理概念和物理规律自认为很熟悉,往往会忽视这些概念内涵的理解,特别是相关物理规律的描述当从特殊到一般、均匀到非均匀情况下所采用的数学手段发生变化,使得许多学生感觉到大学物理的学习比较困难。另一方面,由于中学物理与大学物理在不同的教学环节中有一些区别,大学物理中会介绍当前
大学物理电磁学公式总结.pdf
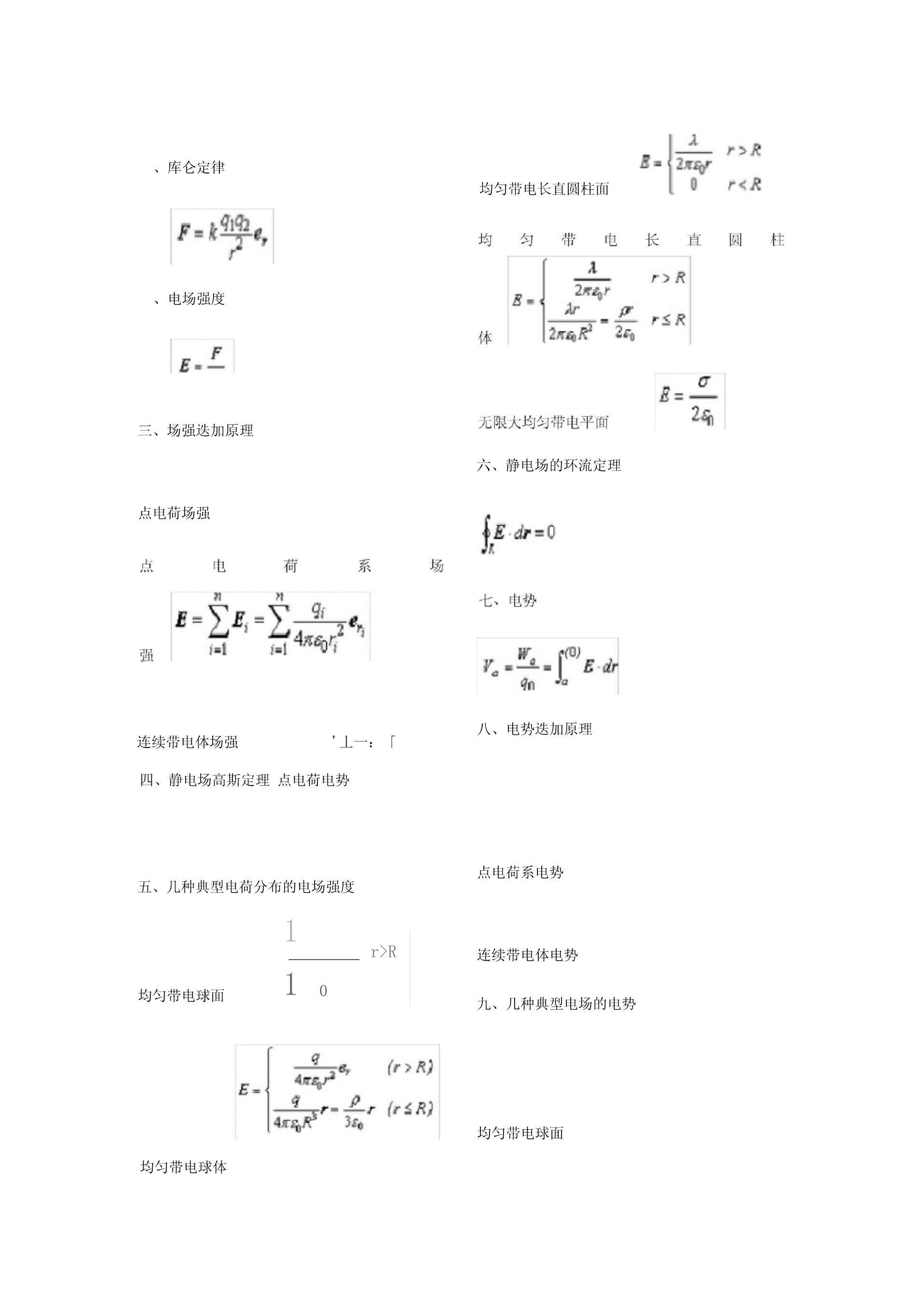
、库仑定律均匀带电长直圆柱面、电场强度三、场强迭加原理六、静电场的环流定理点电荷场强八、电势迭加原理连续带电体场强'丄一:「四、静电场高斯定理点电荷电势点电荷系电势五、几种典型电荷分布的电场强度1r>R连续带电体电势均匀带电球面10九、几种典型电场的电势均匀带电球面均匀带电球体均匀带电长直圆柱面一、库仑定律均匀带电长直圆柱体二、电场强度无限大均匀带电平面六、静电场的环流定理三、场强迭加原理点电荷场强七、电势点电荷系强八、电势迭加原理连续带电体场强点电荷电势四、静电场高斯定理点电荷系电势五、几种典型电荷分布
