
基于MATLAB的汽车平顺性的建模与仿真.doc

可爱****乐多




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料
基于MATLAB的汽车平顺性的建模与仿真.docx
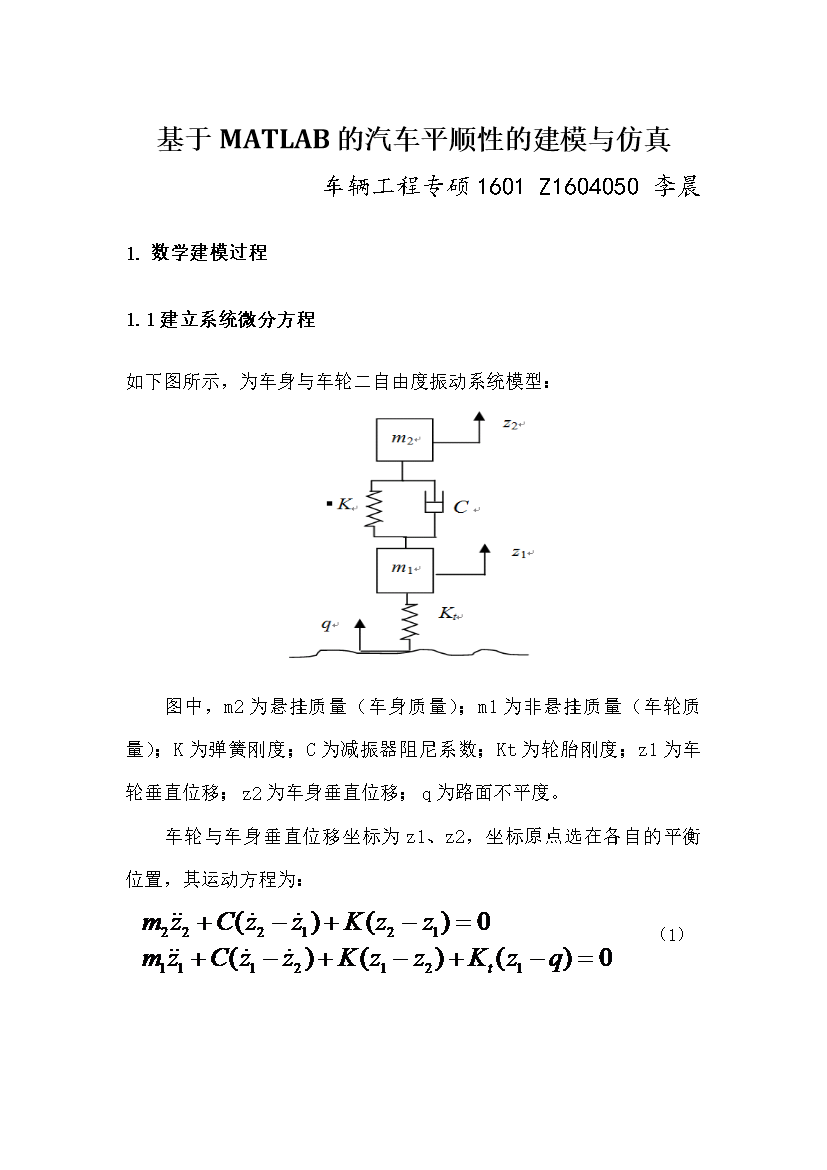
基于MATLAB的汽车平顺性的建模与仿真车辆工程专硕1601Z1604050李晨数学建模过程1.1建立系统微分方程如下图所示为车身与车轮二自由度振动系统模型:图中m2为悬挂质量(车身质量);m1为非悬挂质量(车轮质量);K为弹簧刚度;C为减振器阻尼系数;Kt为轮胎刚度;z1为车轮垂直位移;z2为车身垂直位移;q为路面不平度。车轮与车身垂直位移坐标为z1、z2坐标原点选在各自的平衡位置其运动方程为:(1)

基于MATLAB的汽车平顺性的建模与仿真.doc
基于MATLAB的汽车平顺性的建模与仿真车辆工程专硕1601Z1604050李晨数学建模过程1。1建立系统微分方程如下图所示,为车身与车轮二自由度振动系统模型:图中,m2为悬挂质量(车身质量);m1为非悬挂质量(车轮质量);K为弹簧刚度;C为减振器阻尼系数;Kt为轮胎刚度;z1为车轮垂直位移;z2为车身垂直位移;q为路面不平度.车轮与车身垂直位移坐标为z1、z2,坐标原点选在各自的平衡位置,其运动方程为:(1)1.2双质量系统的传递特性先求双质量系统的频率响应函数,将有关各复振幅代入,得:(2)(3)令:

基于MATLAB的汽车平顺性的建模与仿真.docx
基于MATLAB的汽车平顺性的建模与仿真车辆工程专硕1601Z1604050李晨数学建模过程1.1建立系统微分方程如下图所示为车身与车轮二自由度振动系统模型:图中m2为悬挂质量(车身质量);m1为非悬挂质量(车轮质量);K为弹簧刚度;C为减振器阻尼系数;Kt为轮胎刚度;z1为车轮垂直位移;z2为车身垂直位移;q为路面不平度。车轮与车身垂直位移坐标为z1、z2坐标原点选在各自的平衡位置其运动方程为:(1)

基于MATLAB的汽车平顺性的建模与仿真.doc
基于MATLAB的汽车平顺性的建模与仿真车辆工程专硕1601Z1604050李晨数学建模过程1。1建立系统微分方程如下图所示,为车身与车轮二自由度振动系统模型:图中,m2为悬挂质量(车身质量);m1为非悬挂质量(车轮质量);K为弹簧刚度;C为减振器阻尼系数;Kt为轮胎刚度;z1为车轮垂直位移;z2为车身垂直位移;q为路面不平度.车轮与车身垂直位移坐标为z1、z2,坐标原点选在各自的平衡位置,其运动方程为:(1)1.2双质量系统的传递特性先求双质量系统的频率响应函数,将有关各复振幅代入,得:(2)(3)令:

基于MATLAB的汽车平顺性的建模与仿真.docx
基于MATLAB的汽车平顺性的建模与仿真车辆工程专硕1601Z1604050李晨数学建模过程1.1建立系统微分方程如下图所示为车身与车轮二自由度振动系统模型:图中m2为悬挂质量(车身质量);m1为非悬挂质量(车轮质量);K为弹簧刚度;C为减振器阻尼系数;Kt为轮胎刚度;z1为车轮垂直位移;z2为车身垂直位移;q为路面不平度。车轮与车身垂直位移坐标为z1、z2坐标原点选在各自的平衡位置其运动方程为:(1)
