
永磁同步电机矢量控制系统仿真研究.pdf

文库****品店



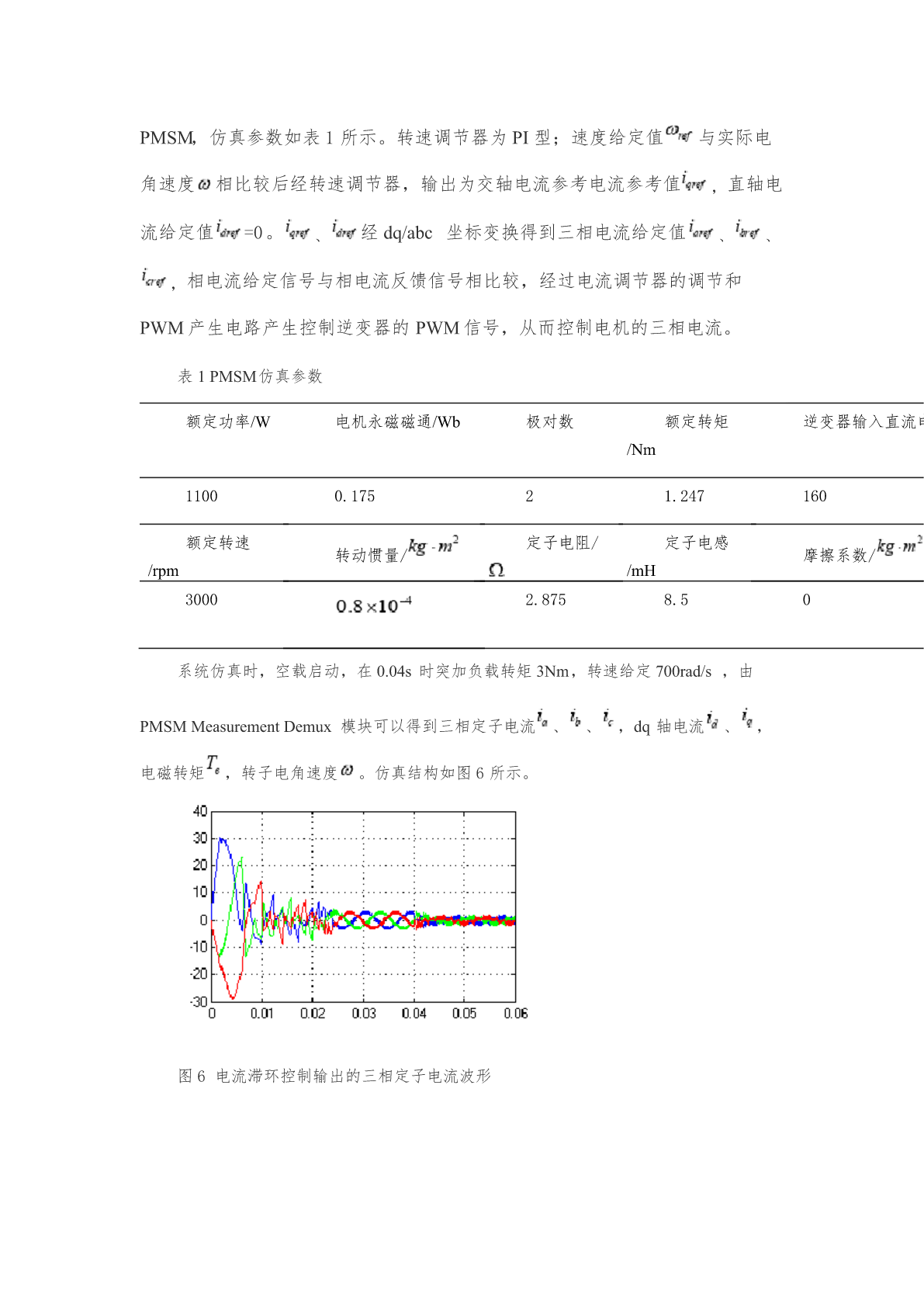

在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

永磁同步电机矢量控制系统仿真研究.pdf
永磁同步电机矢量控制系统仿真研究摘要:随着电力电子、电机制造技术以及新型材料的飞速发展,交流调速理论以及新型控制理论研究的不断深入,永磁交流调速系统在机电一体化、机器人、柔性制造系统等高科技领域中占据了日益重要的地位。永磁同步电动机具有能量转换效率高、体积小,运行可靠性高、调速范围广,动、静特性好等优点,这使得永磁同步电动机技术得到了迅速发展。PWM控制技术从最早追求电压波形正弦,到电流波形正弦,再到磁通正弦,得到了不断创新和完善。本文是在此基础上,参照了众多学者的研究,对永磁同步电机进行了矢量控制的研究

永磁同步电机矢量控制系统建模仿真研究.pptx
汇报人:/目录0102永磁同步电机矢量控制系统的基本原理永磁同步电机矢量控制系统的应用场景永磁同步电机矢量控制系统的研究现状03永磁同步电机矢量控制系统的数学模型永磁同步电机矢量控制系统的仿真模型永磁同步电机矢量控制系统的参数优化04仿真模型的验证与实现矢量控制策略的仿真研究仿真结果的分析与比较05实验平台的搭建与测试实验结果的分析与比较实验结果与仿真结果的对比分析06永磁同步电机矢量控制系统的发展趋势永磁同步电机矢量控制系统面临的挑战与问题永磁同步电机矢量控制系统的未来研究方向汇报人:

永磁同步电机矢量控制及其仿真研究.docx
永磁同步电机矢量控制及其仿真研究永磁同步电机(PermanentMagnetSynchronousMotor,PMSM)是一种在工业和家庭应用中广泛使用的电机类型。它具有高效率、高功率密度和优良的动态特性等优点,因此受到了越来越多的关注和研究。在PMSM的控制中,矢量控制是一种常用的方法。矢量控制是一种以旋转三相坐标系为基础的控制方法,它能够实现电机的高动态性和高静态精度。矢量控制的基本思想是将电机的磁场和电流分解为磁场定向分量和磁场旋转分量,然后通过控制电流的大小和相位来实现对电机的控制。矢量控制技术可

永磁同步电机矢量控制仿真.docx
永磁同步电动机矢量控制仿真1.前言随着微电子和电力电子技术的飞速发展,越来越多的交流伺服系统采用了数字信号处理器(DSP)和智能功率模块(IPM),从而实现了从模拟控制到数字控制的转变。空间矢量PWM调制,它具有线性范围宽,高次谐波少,易于数字实现等优点,在新型的驱动器中得到了普遍应用。永磁同步电机(PMSM)具有较高的运行效率、较高的转矩密度、转动惯量小、转矩脉动小、可高速运行等特点,在诸如高性能机床进给控制、位置控制、机器人等领域PMSM得到了广泛的应用。近几年来,国内外学者将空间矢量脉宽调制算法应用

永磁同步电机矢量控制仿真.docx
永磁同步电动机矢量控制仿真1.前言随着微电子和电力电子技术的飞速发展,越来越多的交流伺服系统采用了数字信号处理器(DSP)和智能功率模块(IPM),从而实现了从模拟控制到数字控制的转变。空间矢量PWM调制,它具有线性范围宽,高次谐波少,易于数字实现等优点,在新型的驱动器中得到了普遍应用。永磁同步电机(PMSM)具有较高的运行效率、较高的转矩密度、转动惯量小、转矩脉动小、可高速运行等特点,在诸如高性能机床进给控制、位置控制、机器人等领域PMSM得到了广泛的应用。近几年来,国内外学者将空间矢量脉宽调制算法应用
