基于多 Agent 强化学习的 Ad hoc 网络跨层拥塞控制策略.pdf

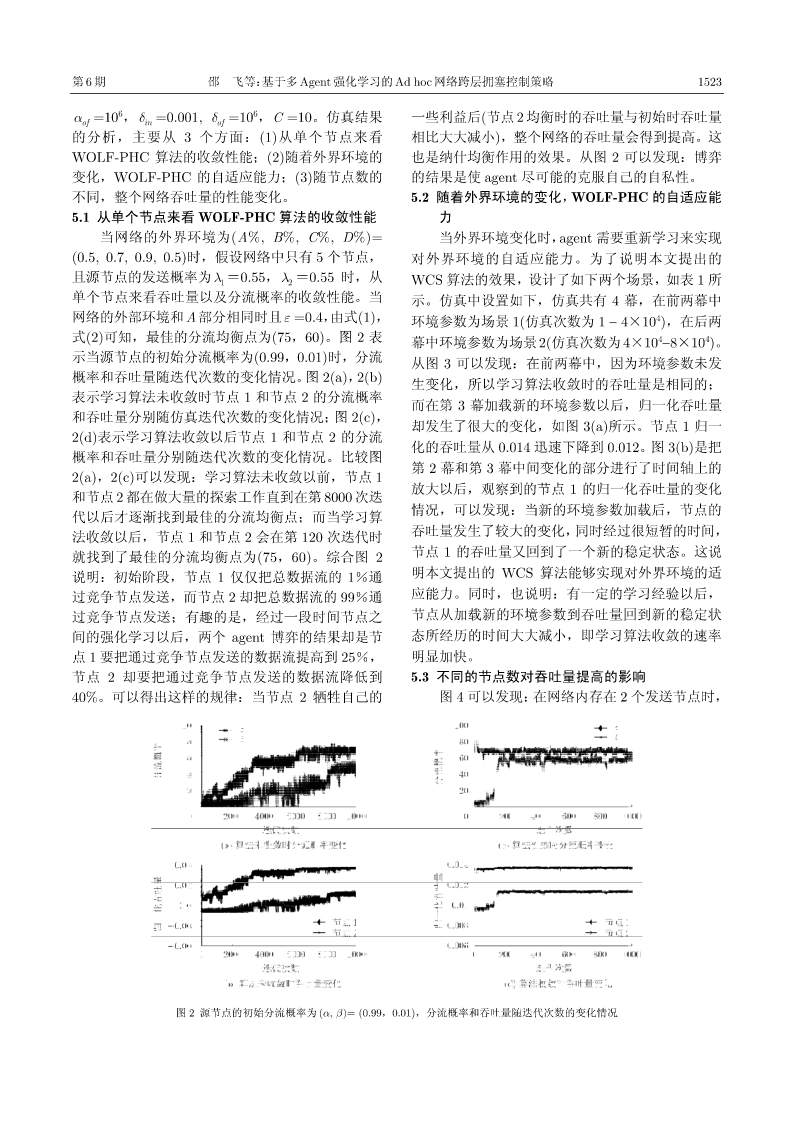
第32卷第6期电子与信息学报Vol.32No.6
2010年6月JournalofElectronics&InformationTechnologyJun.2010

基于多Agent强化学习的Adhoc网络跨层拥塞控制策略

①①②
邵飞伍春汪李峰
①
(西安电子科技大学通信工程学院西安710071)
②
(中国电子系统工程公司研究所北京100141)

摘要：该文首先证明基于MAC层竞争造成的网络拥塞模型中存在纳什均衡点。其次，基于WOLF-PHC学习策
略提出了一种跨层拥塞控制(WCS)机制。它在路由层中选择一对去耦合节点作为转发节点，同时在MAC层对源节
点的发送数据进行分流，从而提高链路的空间重用性。仿真结果表明：在不需要交互任何信息的情况下，通过节点
之间的相互博弈以后，采用WOLF-PHC算法能够找到每个节点的最佳分流概率进而使整体网络吞吐量达到最大
值；同时当外界环境发生改变时，该算法能够较快地找到新的最佳分流概率从而实现对环境的自适应能力。
关键词：Adhoc；拥塞控制；跨层设计；博弈论；WOLF-PHC
中图分类号：TN915文献标识码：A文章编号：1009-5896(2010)06-1520-05
DOI:10.3724/SP.J.1146.2009.01092

ResearchonCross-layerCongestionControlStrategyBasedon
Multi-agentReinforcementLearninginAdhocNetwork
ShaoFei①WuChun①WangLi-feng②
①
(TheSchoolofTelecommunicationsEngineering,XidianUniversity,Xi’an710071,China)
②
(InstituteofChinaElectronicSystemEngineeringCorporation,Beijing100141,China)

Abstract:Inthepaper,theexistenceofanNashequilibriuminthenetworkcongestionmodeinducedbyMAC
layercompetitionisprovedfirstly;Secondly,across-layercongestion-controlmechanismnamedWCSisproposed
basedonWOLF-PHClearningstrategy.WCSselectsacoupleofdecouplednodeasnext-hopnodesatroutinglayer;
Meanwhile,source'strafficisspittedandforwardedatMAClayer,whichimprovesthespacereusingefficiencyof
link.Simulationresultshowsthat:withoutanyexchanginginformation,optimumsplit-flowpointofsourcenode
willbesoughtbyWOLF-PHCinordertomaximizethenetworkthroughput;Furthermore,WOLF-PHCwill
discovernewoptimumsplit-flowpointinordertoadapttonewnetworkenvironment.
Keywords:Adhoc;Congestioncontrol;Cross-layerdesign;Gametheory;Win-Or-Lose-FastPolicyHill
Climbing(WOLF-PHC)
1引言通过非协同不完全信息下的博弈找到最佳分流点。
本文主要研究在带宽受限的Adhoc网络中，节2网络拥塞模型以及Nash均衡点的存在性
点之间如何通过博弈学习而实现最佳的数据分流。
2.1基于MAC层竞争造成的网络拥塞模型
通过对节点自私性和网络拥塞的关系进行建模，在
如图１所示，节点A，B为两个源节点，分别
随机博弈的框架下，将强化学习[1]与对策论相结合，
要给目的节点C，D发送数据。节点E，F为A→C
使节点(也称为agent)通过对各种对策形势的学习
自动掌握如何在不削弱整体网络性能的同时增加自的两个可用中继节点；节点G，H为B→D的两个
己的性能。WOLF-PHC(Win-Or-Lose-FastPolicy可用中继节点。节点F，G处于轻度干扰区域(图１
HillClimbing)算法[2]将“赢否则就要学得更快”策中白色椭圆区域)，节点E，H处于重度干扰区域(图
略扩展到PHC的学习策略中，从而既满足单