3 混合策略纳什均衡(1).pdf

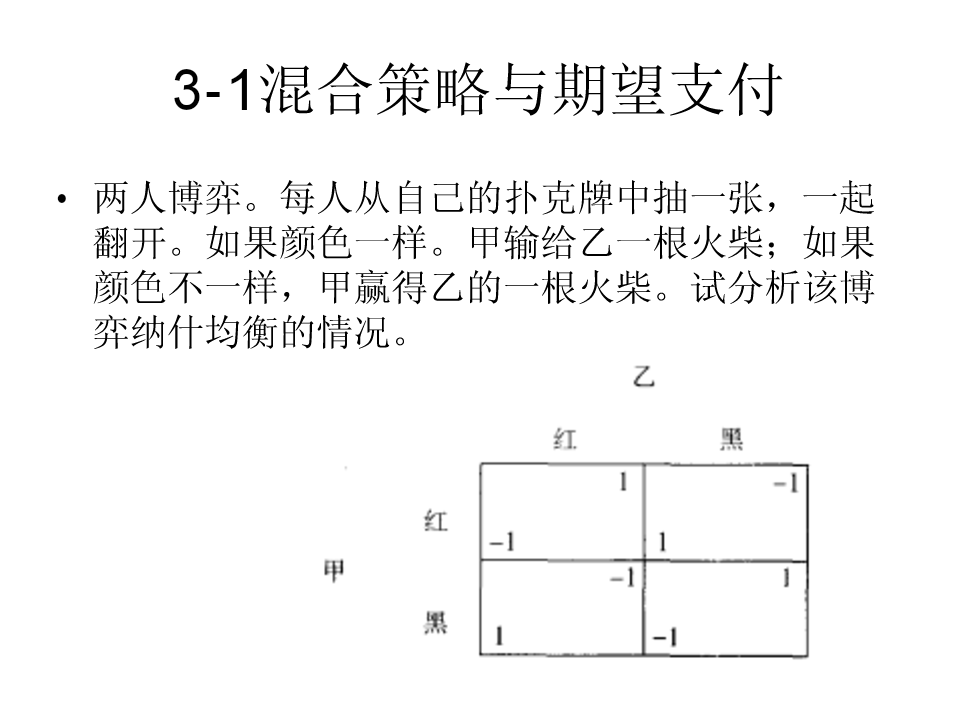
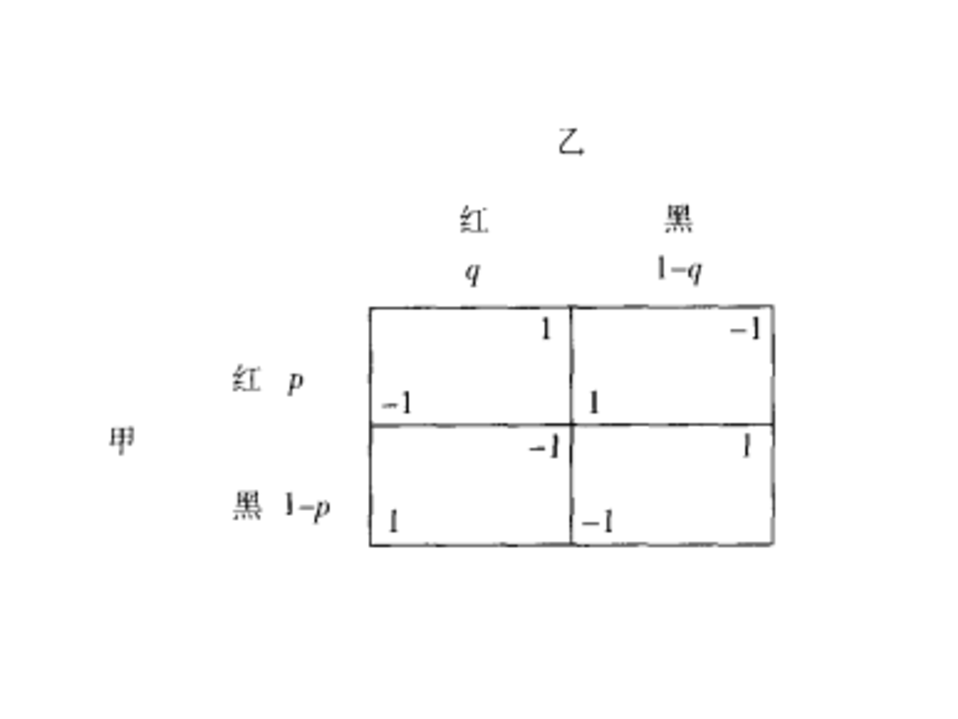
第二章同时决策博弈(2)回顾
•2-7箭头指向法

•2-8纳什均衡的正式定义
–策略集都是实数的开区间且支付函数都是可微
的多元函数
–连续情形纳什均衡的检验方法

•2-9“最后归宿”博弈
•2-10纳什均衡的应用
–古诺竞争模型
–伯川德双寡头竞争模型

•2-11纳什均衡的观察与验证

•2-12弱劣势策略消去法的讨论
–严格纳什均衡和普通纳什均衡
第三章混合策略纳什均衡(1)
•3-1混合策略与期望支付

•3-2反应函数法

•3-3埃奇沃斯图与帕雷托有效
3-1混合策略与期望支付

•两人博弈。每人从自己的扑克牌中抽一张，一起
翻开。如果颜色一样。甲输给乙一根火柴；如果
颜色不一样，甲赢得乙的一根火柴。试分析该博
弈纳什均衡的情况。
混合策略和纯策略

•每个局中人最合理的做法。是随机地出红牌
或出黑牌。然后看能不能凭运气击败对手。
局中人这种随机化自己可选策略的做法，就
是采取“混合策略”的思想。
•混合策略和纯策略
–纯策略是每个局中人具体明确了一个非随机性
的行动计划。
–混合策略是局中人可以按照一定的概率，随机
地从纯策略集合中选择一种纯策略作为实际的
行动。
•例：从局中人甲的角度看，他有出红牌和出黑牌
两种“纯策略”，还有以p的概率出红牌和以1-p的
概率出黑牌的“混合策略”。
–若p=0.4，则甲的混合策略是（p，1-p），即（0.4，
0.6），甲以40%的概率出红牌，以60%的概率出黑牌。
–甲的混合策略(0，1)就是纯策略（只出黑牌）。
–因此，混合策略概念是纯策略概念的推广。

•乙的混合策略是(q，1-q)。就是说乙用q的概率出
红牌，用1-q的概率出黑牌。

•如果一个局中人有三个纯策略可供选择，
选择三种策略的机会加起来是100%。用两
个字母q和r的组合(q,r,1-q-r)就可把所有可
能的策略选择表达出来。
•与混合策略相伴随的一个问题是局中人支付的不
确定性，这就需要期望支付的概念。
•某数量指标的期望值定义：以发生概率作为权重
的所有可能取值的加权平均。

pX11+p2X+2...+npnX
补充：圣彼得堡悖论

•尼古拉斯.伯努利(1713)
•赌博的参与人掷一个硬币，直到出现正面向上为
止。如果第n次掷硬币才出现正面向上，则参与人
得到2^(n-1)美元。人们愿意出多少钱来参加一次
这样的赌博？

∞
nn−1
(1/2)∑×2=1/2++1/2K+1/2=∞
n=1
期望效用理论

•对于圣彼得堡悖论的思考，引导经济学家
提出期望效用理论。
•期望效用理论认为：人们并不直接关心得
到多少钱，而是关心这些钱所能带来的效
用。即人们直接关心的不是不确定性收益
的期望值，而是由不确定性收益产生的不
确定性效用的期望值。
数学语言表达

•如果主体人对确定性收益x的效用为u(x)，那么主体
人对不确定性收益X的效用就为E(u(X))。
•E(u(X))称为X的期望效用，常记为EU(X)。将X看作
自变量，EU(X)称为期望效用函数。
•如果不确定性收益X退化成确定性收益x，则EU(X)=
u(x)，所以EU(X)可以同时表达主体人对确定性收益
和不确定性收益的效用。
•期望效用理论很好地解答了圣彼得堡悖论。
•如果一个主体人对确定性收益的效用函数
u(x)=ln(x)，那么这个主体人从赌博中得到
的期望效用为：

∞
(1/∑2)n×lnn−12=ln2
n=1
回到扑克对色游戏
•在博弈论中，当局中人并不清楚其他局中人的实
际策略选择时，他的支付便具有了不确定性，为
此，他只能通过计算期望支付的方式来预测自己
的得益情况，确定自己的策略选择。
•甲乙的混合策略如图：计算甲乙的期望支付。
(,)U1Ap（）=1qpq−(1+p)−1q+(1−)p+−q(−p1)(−q1)(1)
=pq−p+pq−+q−pq+q−pq
=−4pq+2p+2q1−
2=(p1−2q)+(q2−1)

(,)UpB2(2q=q−1)(2p−−p1)
扩展：二人博弈标准型
n人参与的策略式博弈混合策略定义
•∑i表示局中人i的混合策略空间

p(•=p,...,1ip,...,npi∈∑p),i表示博弈的一个混合策
略组合

(•)pπi(=πip,...,1ip,...,np表示局中人)i在混合策略

组合p(=p,...,1ip,...,np下的期望支付，它是混)
合策略组合p的函数。
3-2反应函数法

•寻找同时决策有限博弈的混合策略纳什均衡
•B的混合策略设定为（q，1-q）时，A的最佳
反应函数是：

(,)UpA2(1q=p−2)(2+q−q1)
•A的混合策略设定为（p，1-p）时，B的最
佳反应函数是：

(,)UpB2(2q=q