基于状态空间模型的控制系统设计.ppt

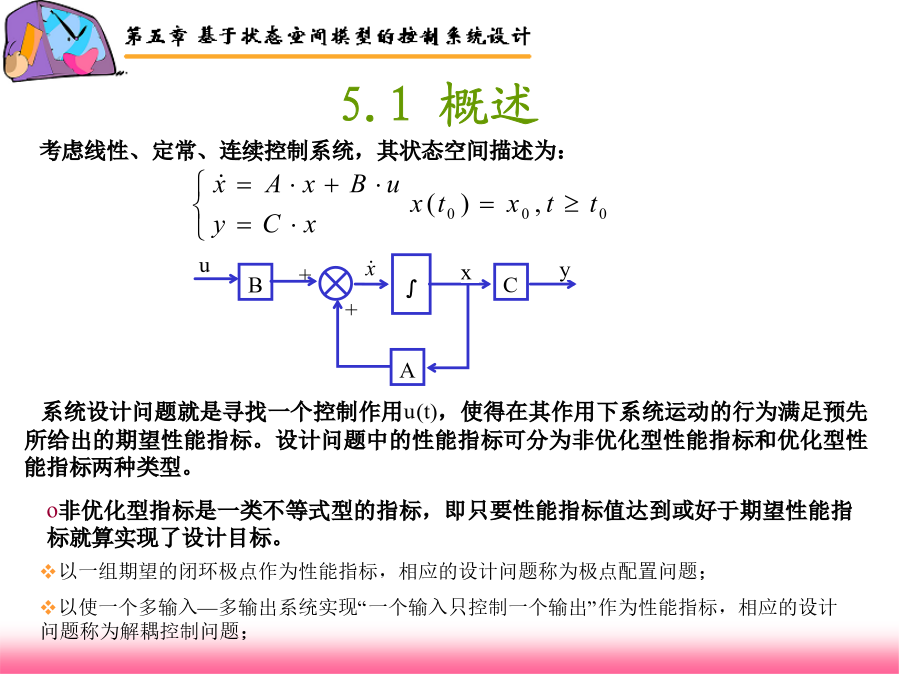
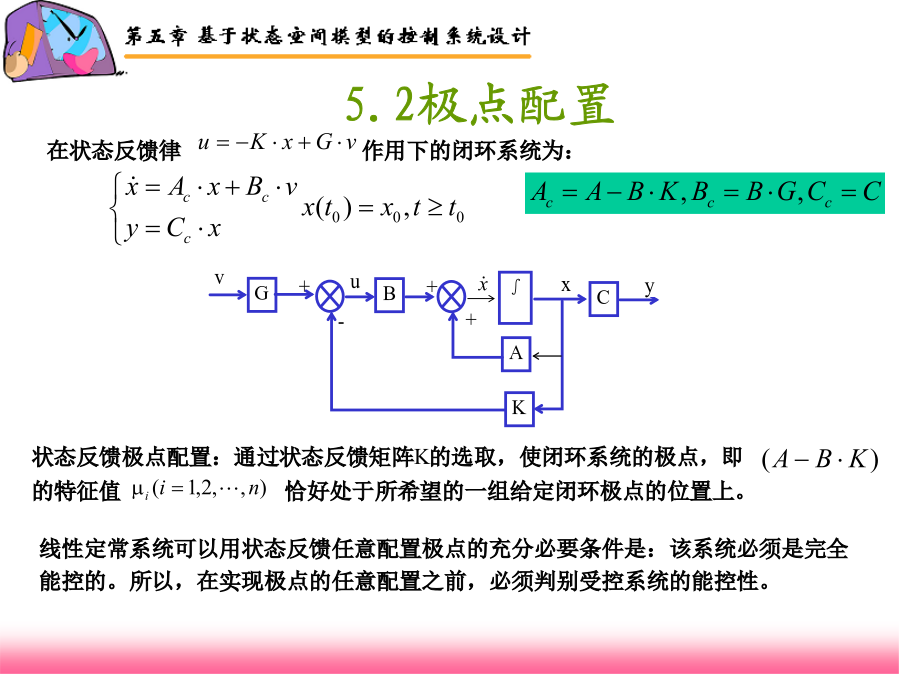
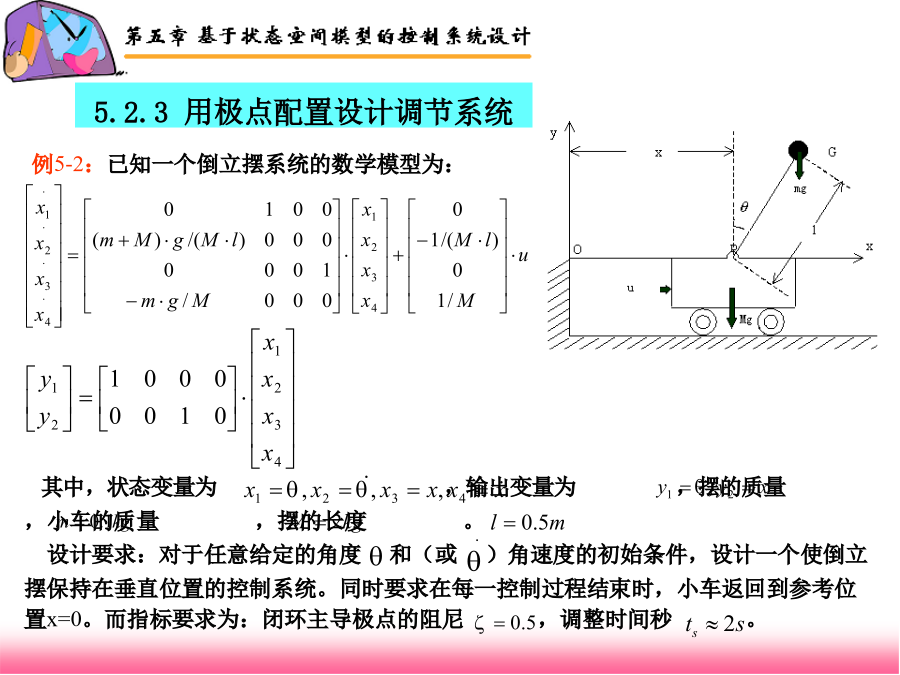
第五章基于状态窨模型的控制系统设计5.1概述优化型指标则是一类极值型的指标，设计目标是要使性能指标在所有可能值中取得极小（或极大）值；5.2极点配置5.2.1单输入系统的极点配置Ackermann算法：状态反馈阵为令，，于是，对于给定，可以求出pitian()函数的调用格式：5.2.3用极点配置设计调节系统解：1、将给定的的值代入上式，得到：5.2.4用极点配置设计伺服系统pp_sifuI()函数的调用格式为：[K,x_ss,y_ss,u_ss]=pp_sifuI(A,b,c,p,v)假定：r=m=1；前馈通道不含积分器；受控系统是完全能控的，且其传递函数在原点处没有零点。且由定义：pp_sifu0()函数的调用格式为：[K,kI,x,y,t,x_ss,y_ss,u_ss,zeta_ss]=pp_sifu0(A,b,c,p,v,t)5.3线性二次型最优控制5.3.1无限时间LQ状态调节问题关于无限时间LQ状态调节问题的鲁棒性有以下结论：对于无限时间定常LQ状态调节问题的最优调节系统，取加权阵则系统的每一个反馈控制回路均具有：（1）至少的相角裕度；（2）从0.5到无穷大的幅值裕度。例5-5：考虑例5-2所示的倒立摆系统，按不含积分器的I型伺服系统设计的方法，倒立摆系统就变成了一个闭环系统，其误差方程为：对于受控系统,其无限时间LQ输出调节问题中的性能指标为：5.3.3最优跟踪问题lqr_c()函数的调用格式为：[P,g,K1,K2]=lqr_c(A,B,C,Q,R,yr)其中{A，B，C}为受控系统的状态空间描述，Q，R为加权阵，yr为参考输出向量5.4解耦控制decoupling()函数实现动态解耦控制算法，decoupling_s()函数实现静态解耦控制算法，其调用格式为：[G,K,L]=decoupling(A,B,C),[vv,K,L]=decoupling_s(A,B,C,p,dd)姚昂坐披读僳钝峨违笨箕埋益炉襟莎胆琉骨场感芭浮疮观丢里紧犬拦钠杉基于状态空间模型的控制系统设计基于状态空间模型的控制系统设计5.5状态观测器设计例5-10：同例5-2的状态空间模型,并将两个极点配置到s=-1,s=-2。怒匆们慌榷沂深秩攘筋俭献虹医冯武库继悄肾据艾缺钟噪谅其堰皆轰琵胳基于状态空间模型的控制系统设计基于状态空间模型的控制系统设计+5.6包含状态观测器的状态反馈控制系统执谗源乡锌隧共啡家逃帆玉背怨抖洱检蚀姑碴欠逮拧施乱词沤诊酱渝挥亲基于状态空间模型的控制系统设计基于状态空间模型的控制系统设计包含状态观测器的状态反馈控制系统的设计分两步走。第一步：按照系统性能指标要求（如：极点配置、线性二次型最优控制、解耦控制等要求），有选择地采用前面几节所讨论的各种方法加以设计，从而满足其系统要求；第二步：在不考虑第一步设计的存在的情况下，独立地设计状态观测器，使之满足其所期望的极点位置要求。在第二步中，可以采用5-5节所介绍的方法加以设计与实现状态观测器。5.6.2基于全维状态观测器的调节器控制系统工具箱中的函数reg()，用来设计基于全维状态观测器的调节器，其调用格式为：Gc=reg(G,k,l)其中G为受控系统的状态空间表示，k,l分别表示状态反馈的行向量k和全维状态观测器的列向量l。Gc为基于全维状态观测器的调节器的状态空间表示。