基于ANSYS梁结构静力分析.pdf

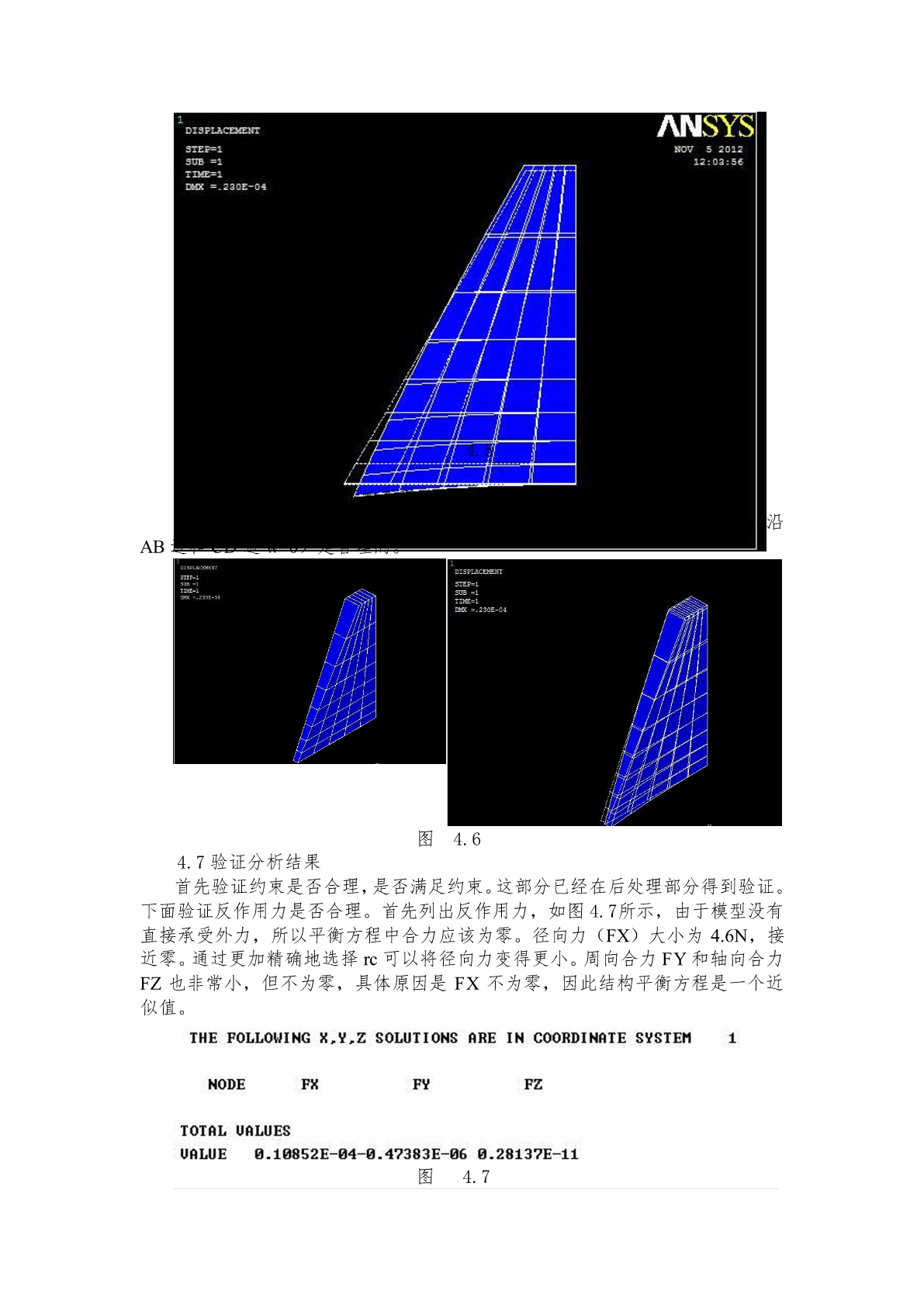
基于梁结构静力分析
ANSYS

李亚锋07209220091001861

摘要：采用大型通用软件ANSYS，对梁结构受弯矩力时工况进行三维有限
元静力分析，计算结果，分析梁体应力分布情况。

关键词：梁结构；ANSYS；有限元；静力分析

0引言

梁结构是生活中常见的结构，为了全面了解梁结构在受到弯矩力时梁体
应力分布状态，采用ANSYS三维有限元对梁结构进行工况静力计算，分析
梁体应力、位移情况。

1概况
1.1梁体的结构与受力
梁的截面形状为梯形截面，各个截面尺寸相同。两端受弯矩沿中性面发
生弯曲，如图1-1所示。利用ANSYS软件对此梯形截面梁进行静力学分析，
以获得沿梁AA截面的应力分布情况。

A

A-A截面
MAM

r
θ

图1-1梯形截面梁受弯矩弯曲模型
1.2问题分析
由于此问题不是轴对称的，梁上各点位移呈圆弧状，有弯曲半径和弯曲中
心，所以采用三维实体单元要比采用轴对称单元好一些。其几何形状可以通
过柱坐标建立。
1.2.1合理简化模型
由于梁弯曲部分的应力不随θ变化，所以可以适当简化模型，取图1-2所
示的切片。AB和CD边夹角为5°。

14mm
DB

D,BM/2M/2

M
88mm
2＃面1＃面

C,A
r
c
CA
r,u
65mm
r,u
对称面44mmθ,γ

Z,w旋转轴5°

图1-2分析切片
由于不知道切片两侧截面上轴向应力的分布情况，所以只能将弯矩M直接
作用在简化模型上。在定义位移约束时仍认为切片两侧保持平面，切片两端只受
纯弯矩载荷，即切片端面不受外力载荷。通过有限元分析可以得到受弯矩切片端
面处的应力分布情况。因应力与所受弯矩呈线性关系，所以截面上的应力与切片
两端面所受弯矩紧密相关。当值不变时，梁的截面上点、、和对称
MpzABCD
分布，所以，分析梁截面时只需取截面的一半。
1.2.1描述模型的边界条件
任意节点处沿u（径向）、v（环方向）、w（轴向）的约束情况如表1-1所示。
表1-1约束条件
1＃面（Face1）2＃面（Face2）
U=0（节点A）无
=0（所有节点）=0.0001(-（所有节点）)
VVrcr
W=0（沿AB边）W=0（沿CD边）

切片上所有节点均被约束。A节点处，u=0可阻止切片沿r方向做刚体运动；
1＃面上所有节点v=0可防止1＃面做圆周运动，对于ABCD由w=0保证切片模
型的对称性；2＃面上保证2＃面绕=面转动时，2＃面保持平面。比例系
BCrrc
数0.0001，这是随意取的，没有特别含义。开始时，不知道的确切值，由于
rc
对应的是纯弯矩，所以节点处的反作用力为零。假设开始时，
rcARarc=60mm
或，则两个值对应的分别为和。根据线性推断，当
rc=70mmrcRa2001N357N
时有。所以，在分析过程中，取（为了分析过程简
Ra=0rc=72.2mmrc=72.2mm
洁，所以在这里给出值，实际问题分析中，读者只能自己确定值）。
rcrc

2有限元模型的建立
2.1选择单元和定义实常数、材料属性
由于采用柱坐标进行三维实体分析，所以选择的单元为8节点6面体单
元。
由于分析不需要定义实常数，因此可以选择默认值。
定义弹性模量和泊松比：
杨氏模量：200e9泊松比：0.3
2.2定义几何参数
根据切片模型，首先定义切片顶点的8个关键点，然后通过关键点生成切
片实体模型。在柱坐标系中生产所需关键点。由于4个关键点是模型图上的A、
B、C、D，另外4个是有同样的r和θ但没有显示出来的z轴方向上的与前4个
关键点对应的关键点。因此，需要通过模型几何参数创建。
通过参数定义几何实体的操作如下：
R1=44e-3R2=R1+88e-3Z1=65e-3Z2=14e-3

2.3定义关键点
由于几何模型将在柱坐标中创建，所以首先要将坐标系转换到柱坐标。
注意：当当前坐标系为柱坐标时，输入提示菜单中的X、Y和Z对应柱坐标
的r、θ（单位为度）和Z。
关键点坐标参数如下：
1＃关键点X=R1，Y=90，Z=0
2＃关键点X=R1，Y=95，Z=0
3＃关键点X=R1，Y=95，Z=Z1
4＃关键点X=R1，Y=90，Z=Z1
5＃关键点X=R2，Y=90，Z=0
6＃关键点X=R2，Y=95，Z=0
7＃关键点X=R2，Y=95，Z=Z2
8＃关键点X=R2，Y=90，Z=Z2

2.4生成切片模型
通过已定义的8个关键点生成实体模型：首先连接底部的关键点，然后连
接顶部的关键点。这些操作均需在笛卡儿坐标系中进行。通过连接关键点而成的
线为直线，即切片的边为直边。此处需要这些边为直边，而柱坐标系中生成的线
却是曲线。
依生成关键点的顺序依次选择关键点，即可得到切片实体模型，结果如图
2.1所示。