
图的定义和术语及存储结构.ppt

as****16

亲,该文档总共35页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料
图的定义和术语及存储结构.ppt
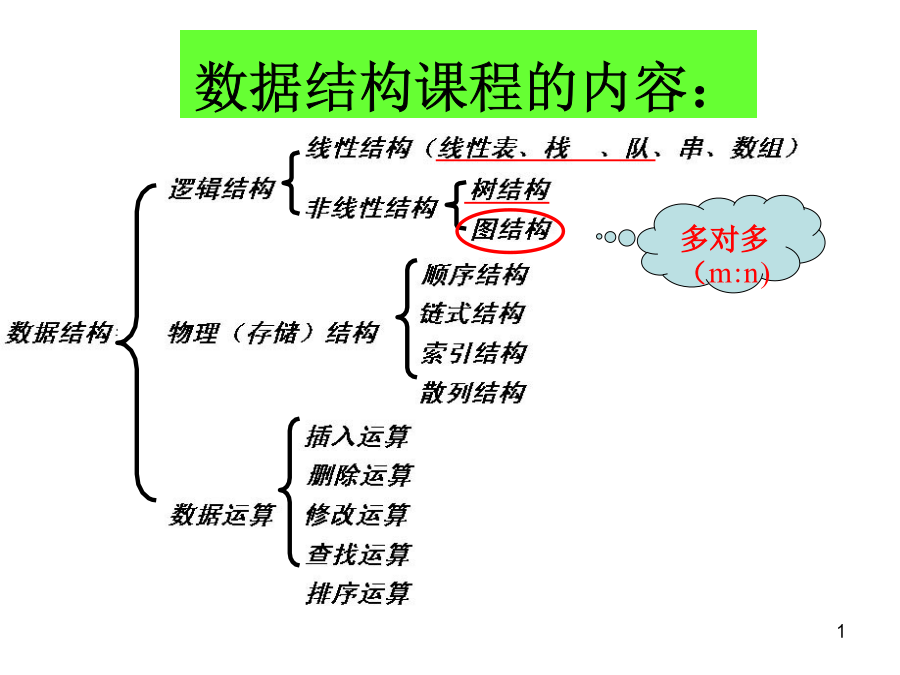
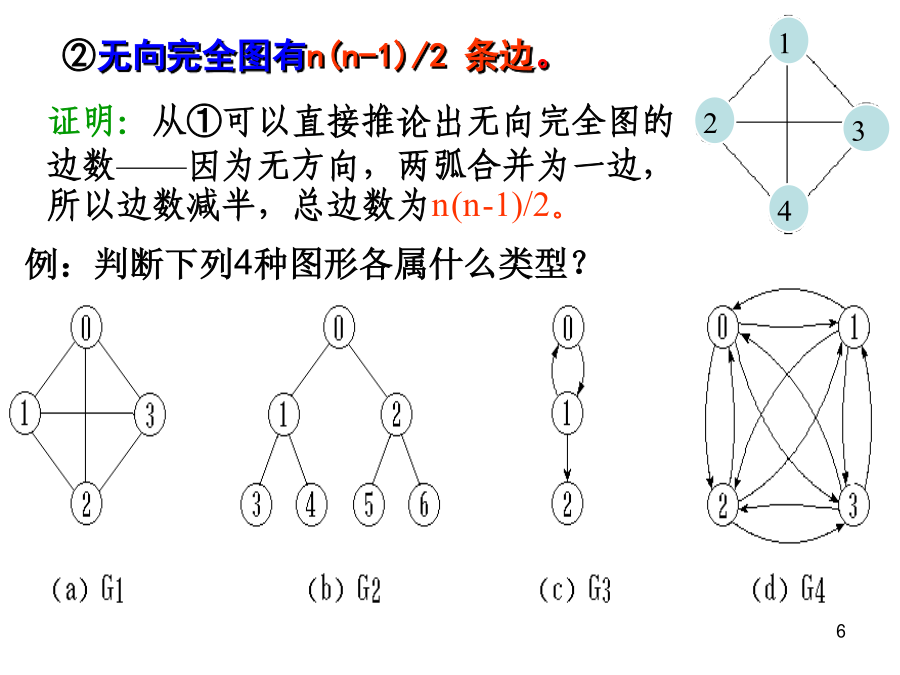
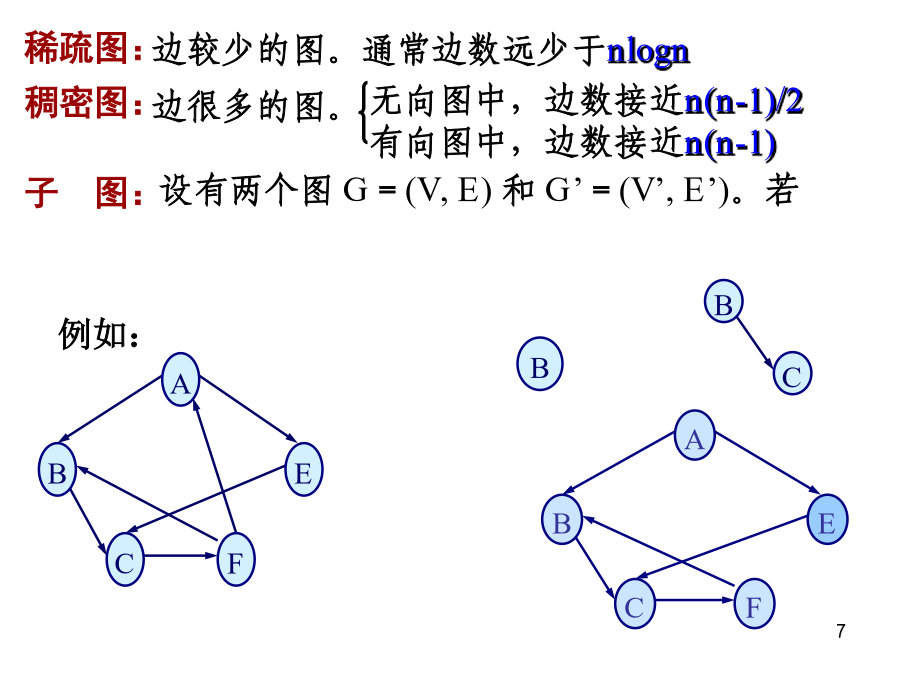
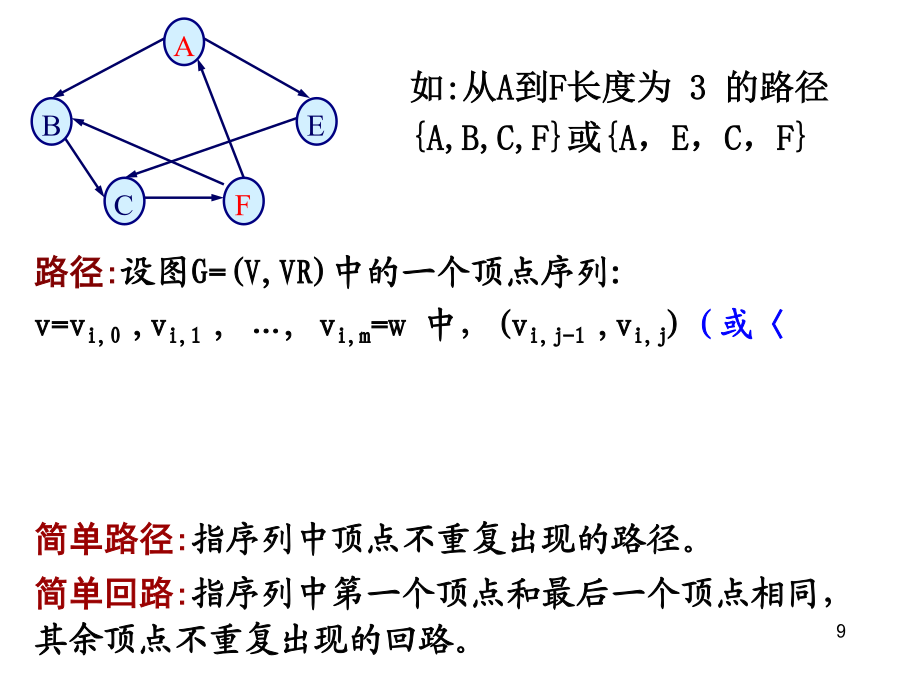
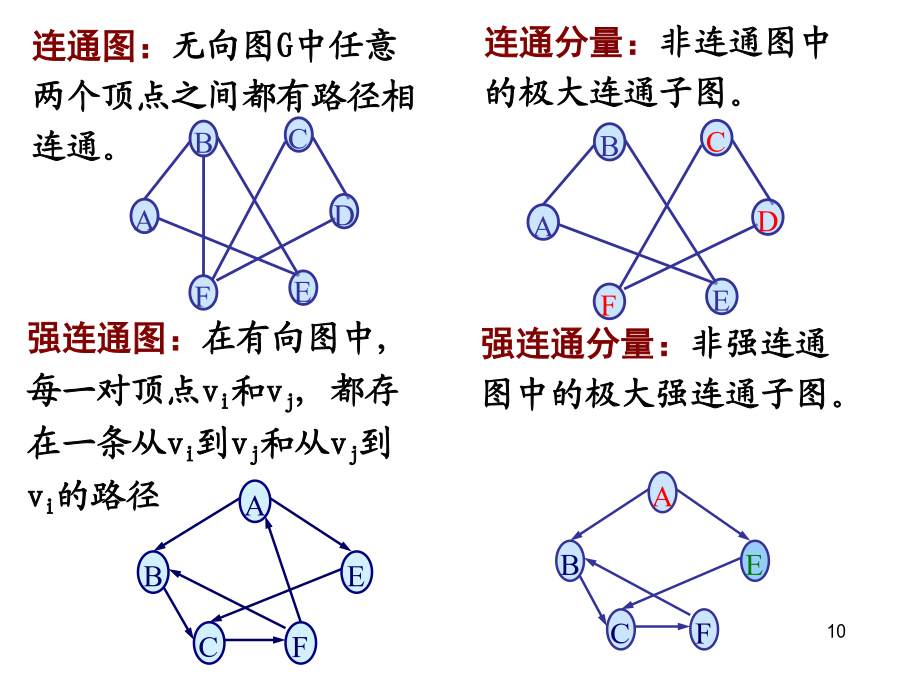
数据结构课程的内容:7.1基本术语7.2存储结构7.3图的遍历7.4图的连通性7.5图的应用7.1图的基本术语EB证明:从①可以直接推论出无向完全图的边数——因为无方向,两弧合并为一边,所以边数减半,总边数为n(n-1)/2。稀疏图:稠密图:A路径:设图G=(V,VR)中的一个顶点序列:v=vi,0,vi,1,…,vi,m=w中,(vi,j-1,vi,j)(或〈vi,j-1,vi,j〉)VR1≤j≤m,则称从顶点v到顶点w之间存在一条路径。路径长度:路径上边(或弧)的数目。连通图:无向图G中任意两个顶点

71 图的定义和基本术语 71 图的定义和基本术语.ppt
第七章图图(Graph)是较线性表和树更为复杂的结构。图中任意数据两个元素之间都可能相关。7.1图的定义和基本术语7.1图的定义和基本术语(续一)子图:G=(V,{E})和G1=(V1,{E1})若V1属于V,E1属于E则G1是G的子图7.1图的定义和基本术语(续三)7.2图的存储结构7.2.1数组表示法数组表示法(邻接矩阵)网及其邻接矩阵7.2.2邻接表---链式存储结构邻接表的链式存储结构示意图7.3图的遍历7.3.1深度优先搜索深度优先搜索算法7.3.2广度优先搜索voidBFSTraverse(G

图的定义和术语.ppt
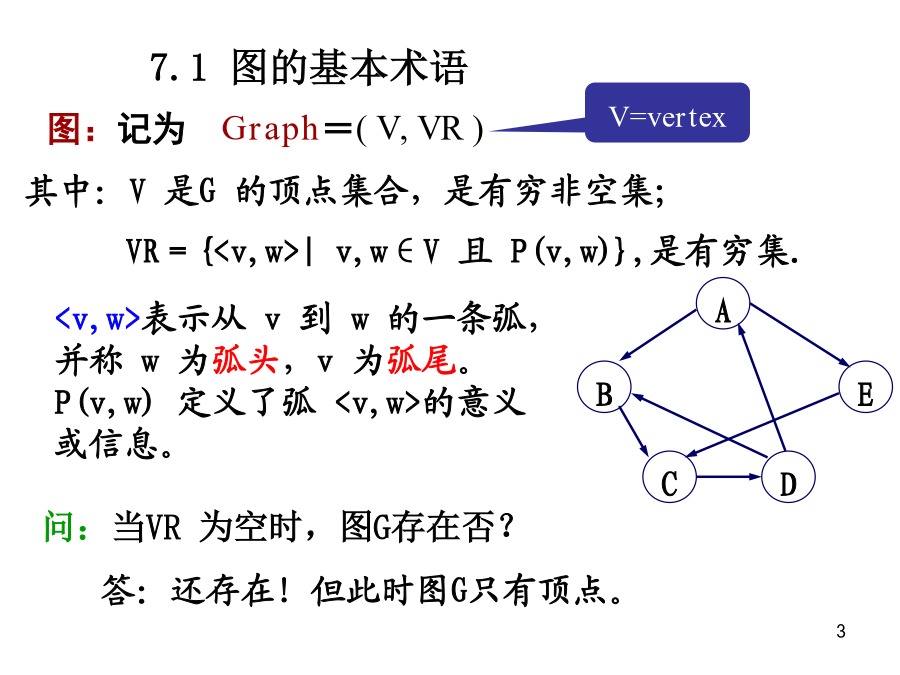
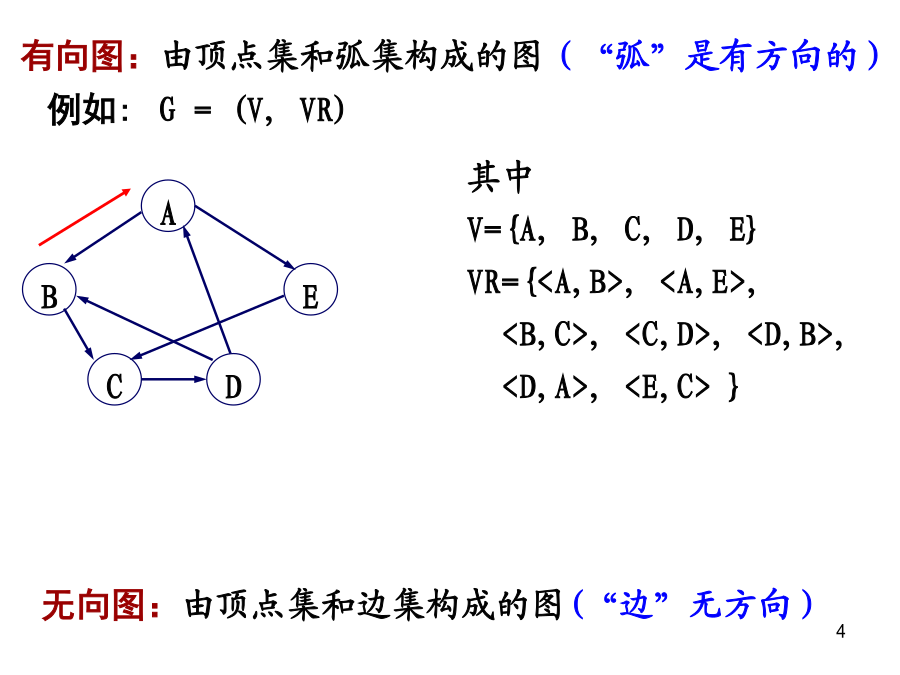
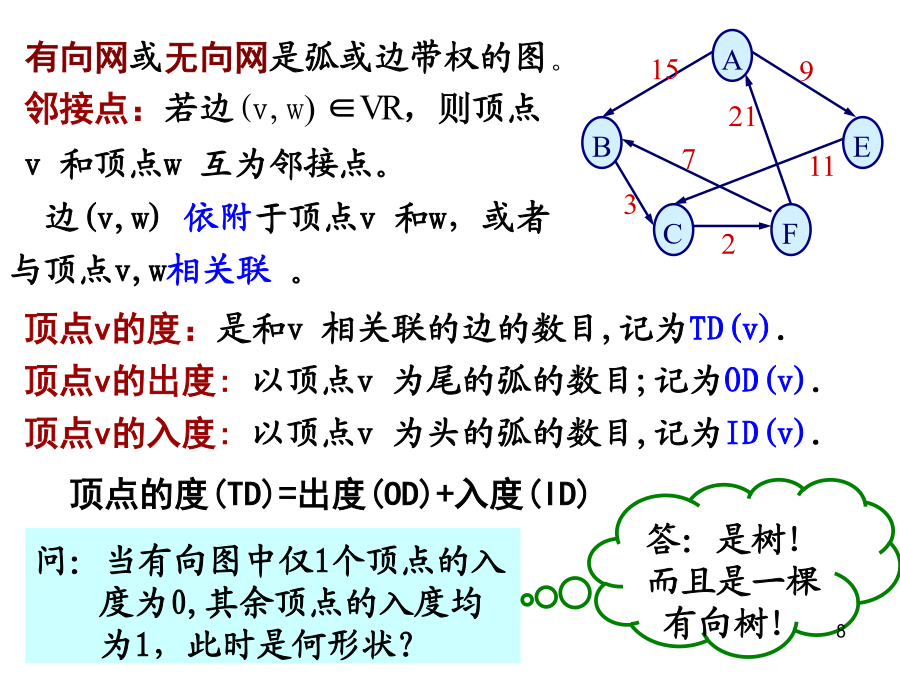
第七章图7.1图的定义和术语基本术语:1.有向图与无向图在有向图中,顶点对<v,w>是有序的。在无向图中,顶点对(x,y)是无序的。有向边又可称为弧,<vi,vj>中vi称为弧尾或初始点,vj称为弧头或终端点。2.邻接点及关联若无向图中存在边(v,u),则称顶点v和u互为邻接点;边(v,u)依附于顶点v和u;或者说边(v,u)和顶点v和u相关联。3.顶点的度、入度、出度在无向图中:顶点V的度=与V相关联的边的数目在有向图中:顶点V的出度=以V为狐尾的有向边数顶点V的入度=以V为狐头的有向边数顶点V的度=V

图的定义和术语(5).ppt
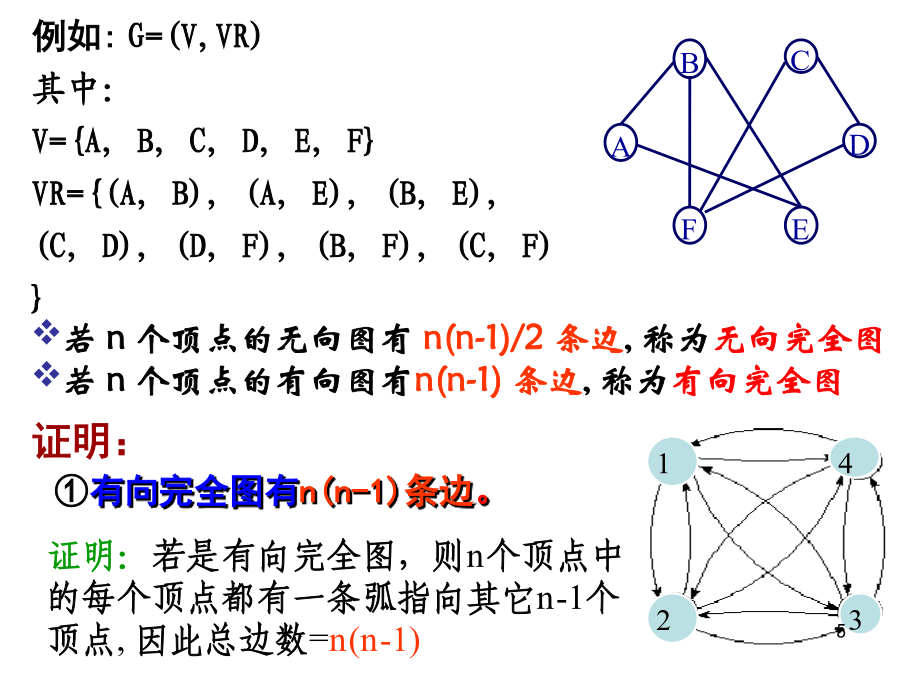
第六章图例有向完备图——n个顶点的有向图最大边数是n(n-1)无向完备图——n个顶点的无向图最大边数是n(n-1)/2权——与图的边或弧相关的数叫~网——带权的图叫~子图——如果图G(V,E)和图G‘(V’,E‘),满足:V’VE’E则称G‘为G的子图顶点的度无向图中,顶点的度为与每个顶点相连的边数有向图中,顶点的度分成入度与出度入度:以该顶点为头的弧的数目出度:以该顶点为尾的弧的数目路径——路径是顶点的序列V={Vi0,Vi1,……Vin},满足(Vij-1,Vij)E或<Vij-1,Vij>E

数据结构第7章图1图的定义和术语.ppt
数据结构DataStructures基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语基本术语图的抽象类型定义图的抽象类型定义图的抽象类型定义图的抽象类型定义图的存储结构图的数组(邻接矩阵)存储表示图的数组(邻接矩阵)存储表示图的数组(邻接矩阵)存储表示图的数组(邻接矩阵)存储表示图的数组(邻接矩阵)存储表示网(带权图)的邻接矩阵图的邻接矩阵图的数组(邻接矩阵)存储
