具有种群Logistic增长的SIR模型的稳定性和Hopf分支.pdf

2024-07-09

10

406KB

一类具有种群Logistic增长的SIR传染病模型的稳定性.pdf

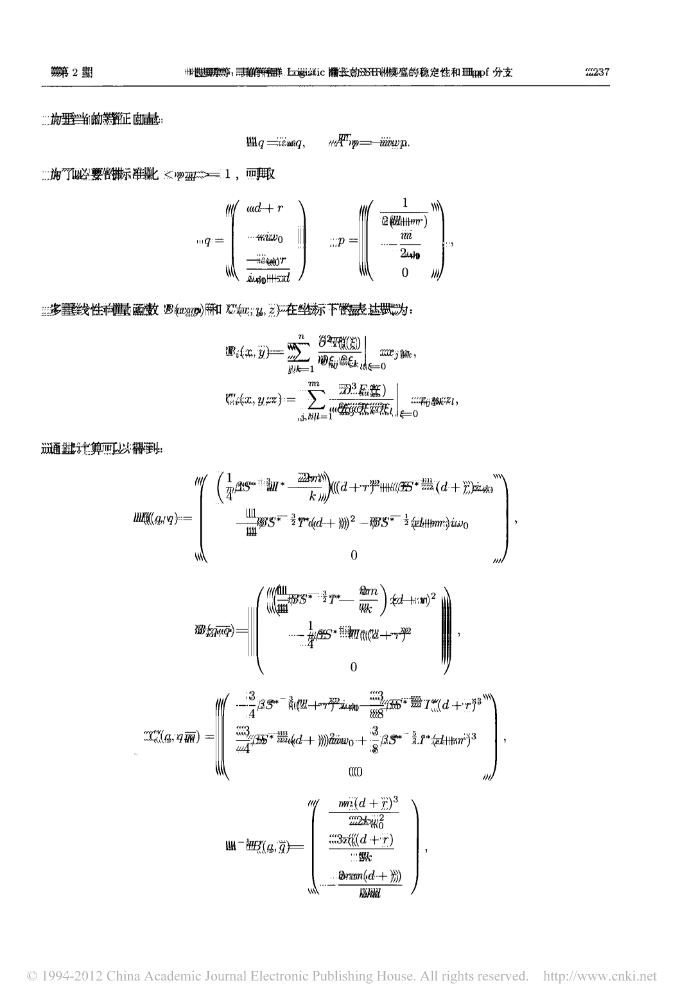
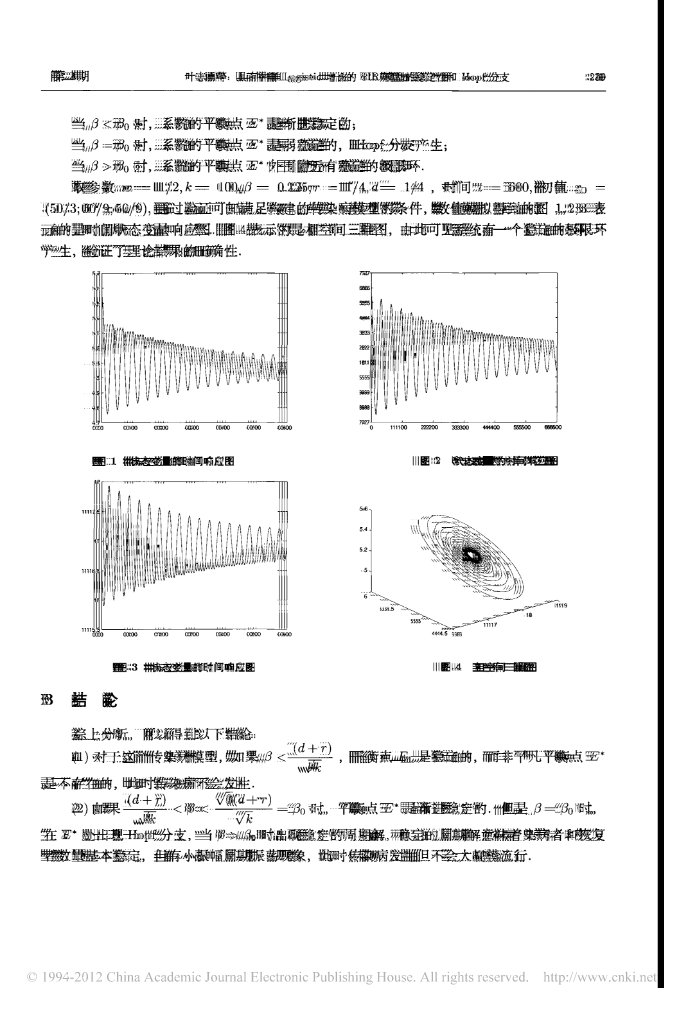
第30卷第1期贵州师范大学学报(自然科学版)Vol．30．No．12012年1月JournalofGuizhouNormalUniversity(NaturalSciences)Jan2012文章编号:1004—5570(2012)01－0064－06一类具有种群Logistic增长的SIR传染病模型的稳定性＊宫兆刚，蔡江涛，阳志锋(衡阳师范学院数学与计算科学系，湖南衡阳421008)摘要:研究一类具有种群Logistic增长的SIR传染病模型，应用微分方程定性理论，分别得到了该系统无病平衡点、地方病平衡

2024-07-09

10

456KB

具有时滞的流体流拥塞控制模型的稳定性及Hopf分支分析.docx

具有时滞的流体流拥塞控制模型的稳定性及Hopf分支分析稳定性和Hopf分支分析是流体流拥塞控制模型研究中重要的内容。本文将从理论和实践两个方面探讨具有时滞的流体流拥塞控制模型的稳定性及Hopf分支分析。一、研究背景在交通流系统和网络流系统中，流体流拥塞控制模型是一种常用的分析工具。然而，当系统存在时滞时，传统的流控制模型无法准确描述系统的行为，因此需要更加复杂的模型来研究具有时滞的流体流拥塞控制问题。二、稳定性分析稳定性是研究流体流拥塞控制模型的重要指标之一。对于具有时滞的系统，稳定性的分析变得更加困难。

2024-10-31

5

10KB

具有时滞的HIV体内感染模型的Hopf分支与稳定性分析.docx

具有时滞的HIV体内感染模型的Hopf分支与稳定性分析本文将探讨具有时滞的HIV体内感染模型的Hopf分支与稳定性分析。HIV是一种严重威胁人类健康的病毒，它袭击人体免疫系统，导致患者免疫力下降，出现各种免疫缺陷症状。因此，研究HIV感染的动力学模型及其稳定性分析对于治疗和预防HIV感染具有重要意义。传统的HIV感染模型通常是基于免疫过程与病毒扩散过程之间的交互作用来描述病毒传播的过程。在这种模型中，通常假设病毒和免疫细胞之间是一种竞争关系。然而，现实中HIV的感染过程常常具有时滞性质，即病毒在感染宿主细

2024-10-15

5

11KB

基于Logistic增长和心理作用的SIR传染病模型的渐近分析.docx

基于Logistic增长和心理作用的SIR传染病模型的渐近分析疫情对于人类的影响是不可避免的。随着现代交通网络的不断发展和人类活动的频繁交流，传染病的爆发和流行已经成为了全球性的问题。在这种情况下，控制疫情的传播是人类社会不得不面对的重要问题。SIR模型是一种描述传染病传播的经典数学模型，其可以用于预测传染病的爆发和流行，并有助于制定相应的预防和控制策略。本文将基于Logistic增长和心理作用的SIR传染病模型做出渐近分析，并探讨其在传染病预测和控制方面的应用。首先，我们需要了解SIR模型的基本原理。S

2024-10-27

5

11KB