线性回归模型中自变量选择问题.pdf

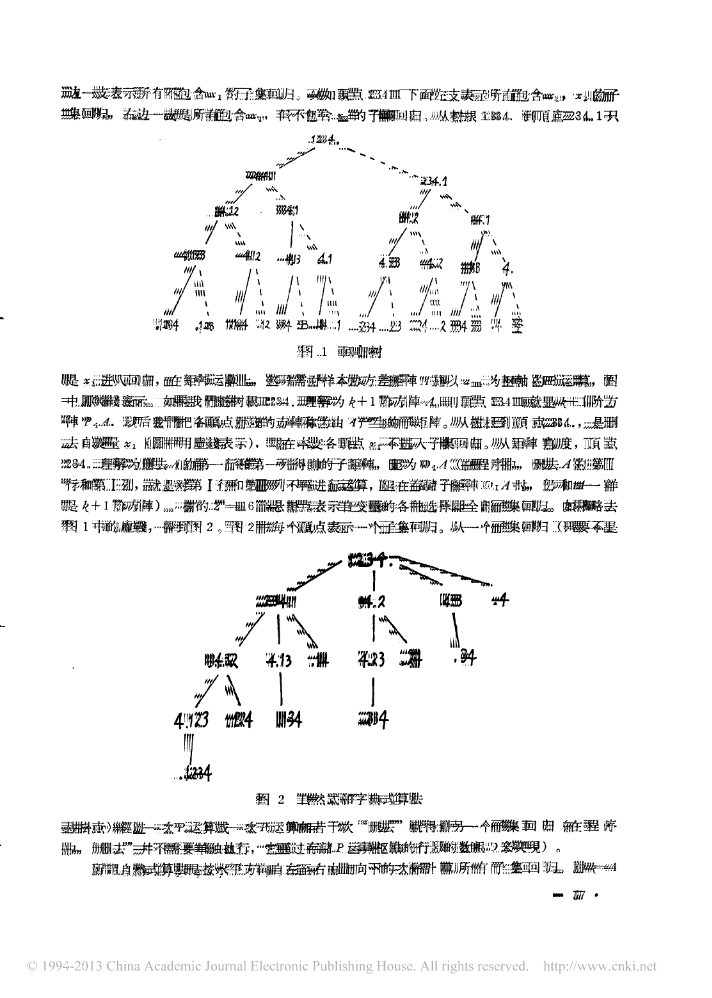
第10卷1期中国科学技术大学学报1980年

线性回归模型中自变量选择问题

不
‘子拜
~.抓}内月口二

(一)回归自变量的选择问题

。
在一个大型回归周题中,可供选择的自变量为数很多国内地鬓工作者使用的“趋势面

。。
分析”,自变量可多达二十多个在将回归固题用于气象予报方面,也存在这种尚题在国
外,将回归分析用于污染因子与死亡率的关系研究中,在汽事役蔚因子与每公里耗油率的关

。
系的研究中,所用的自变量在十到二十个之简据报导,在有些周题中涉及的自变量个数有

。
可能达到50一70个之多
因此,在实用回归分析的研究中,关于从一大批可能的自变量中把真正最重要的那些自
变量挑选出来的周题,一直是一个很受重视的周题。这种挑选的意义,远不在于仅从淤算的

。、
角度着眼实际上,所建立的回归方程的稳定性予报的精度,与这种挑选工作有很密切的

。、
关系而且,通过这种挑选,可以对自变量与因变量的关系自变量之简的关系获得不少有

。
用信泊,一这点应当看作是回归分析的主要目的之一

’
‘
近二十年特别是近十年来,对回归自变量的选择固题,数理杭静工作者和实用抚爵工作

。
者都作了不少工作理输方面的主要成就是提出了一系列的选择准则,对它们的就静性臀作

一。
了一些分析研究,为在实际应用中处理这个尚题提供了一定的理瑞浓扼但这方面的拮果,

。
整个靓来,还处在相当初步的阶段由于阴题的困难,要取得实鬓性进展,还需作很大努

。。
力另一方面的尚题是寻找良好的静算方法由于牵涉到极大量的静算,为了使理湍成果付
藉实用,这是一个必需解决的远非视而易举的尚题,在这方面,近年来也取得了很大的进
展。
在十多年以前,关于选择回归自变量的淮8J,几乎全是基于残差平方和,爵算方面IJ是

。,
用逐步回归(包括向前法和向后法)近年来提出的某些选择准则例如比较受重砚的,由

一
,,,,
M泪肠\毕‘」提出的所谓c,准则也是基于残差平方和另外一些例如所稠P找ESS准
则,还有lloerl等人「2」的岭回归法,以及种种形式的主成份分析法等,则是基于其它的考

、。。
虑〔3118」是关于这方面的粽合性介貂

,。
不湍怎样基于残差平方和的准glJ,现在看来仍属于最重要的一类如果基于这个准
则,就必须处理这样的朋题:投全部自变量有左个,对任何户,1〔p一左,找出残差平方和

、。一
最小次小⋯⋯前若干个(例如,个),个白变最的机由于可能的粗数c,二
·
‘二J,·,~,卜‘
二__一一一-一一P!(左典一,/)一!

。
仕往极大,在缺乏有效的算法时难于实现,逐步回归往往被用来作为一种近似虽然这个方法
起过重要作用且现在也未丧失其意义,但近年来的研究表明,这个方法有着一些缺陷。从理
渝上靓,其中所用的F检墩是建立在不正确的基础上的,从应用上靓,它井不能保征挑出最优
的(残差平方和最小的)p自变量粗(国外报导的一个例子表明,差别能达到37%之多),

。
另一更大的缺陷是不适合用于分析自变量与因变量及自变量之简的关系

,
由于上述原因近年来在国外对寻找残差平方和最小(及若干个按序排列最小)的子集

】
,。、
回归(即所稍最优子集回归)的有效爵算方法抬予很大的注意L3’〔‘〕〔’1Calside‘1965)

、·、·、
Se},arzoff(1965)FL,lnival(1972)入I〔,:gin(1972)FLlrnival和Wilson(2974)〔‘l相

。
撇提出了一些算法和程序,看来以Ftl’lival和Wiloon(197劝的程序为最优本文对

,
Flrnival的算法进行了归钠分析衬渝了它们的性臀,并以其子程序为基础抬出了扑算前

。、
q个最优子集回归的完整程序对这些回归,部算出残差平方和回归系数的最小二乘估静

。。
及其方差利用这些歌息我们可以进一步分析自变量的重要性及其相互关系

(二)计算问题

由于从掩个自变量中选择p个的方法多达c露种,不难毅想,若不按一种粗积良好的方
式进行爵算,则补算量可能达到不现实的地步,解决这个困难的基本方法,就是众所周知
的,在逐步回归中使用的那个规IlJ,它使得在原有的基础上加进或弃却一个自变量时,只需
对当时的协方差障作一种筒单的p运算(晃附录1),即使这样,也还有两个固题要解决:
一是编排一种合适的次序,使能用最少个数的p运算来算出任一个自变量子集的重要的回归

。
抚静量(残差平方和,系数估爵及其方差,协方差等)另一个周题是,一个矩障的元素握
过反复的p运算,累积视差不断增加,考虑到在自变量子集的选择中涉及到极多次数的尸运
算,如不对这个尚题加以充分的考虑并作出相应的安排,则上述累积视差最后将便静算桔果

。
完全失其这里所介貂的程序对这个尚题有较好的处理,它是基于以下的想法