
241 圆的有关性质(第5课时).ppt

dc****76





在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

241圆的有关性质(第5课时).ppt
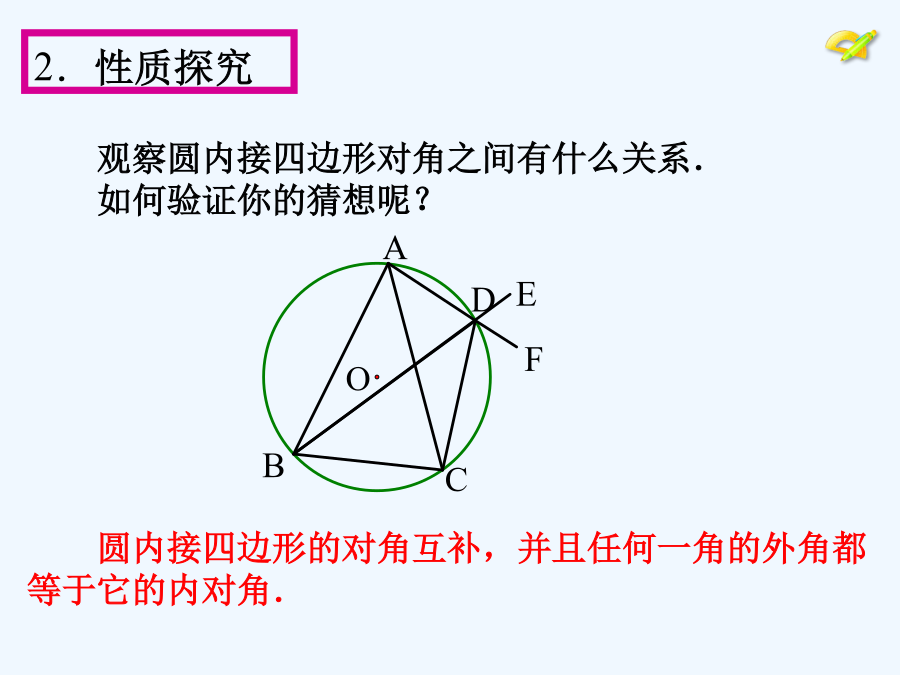
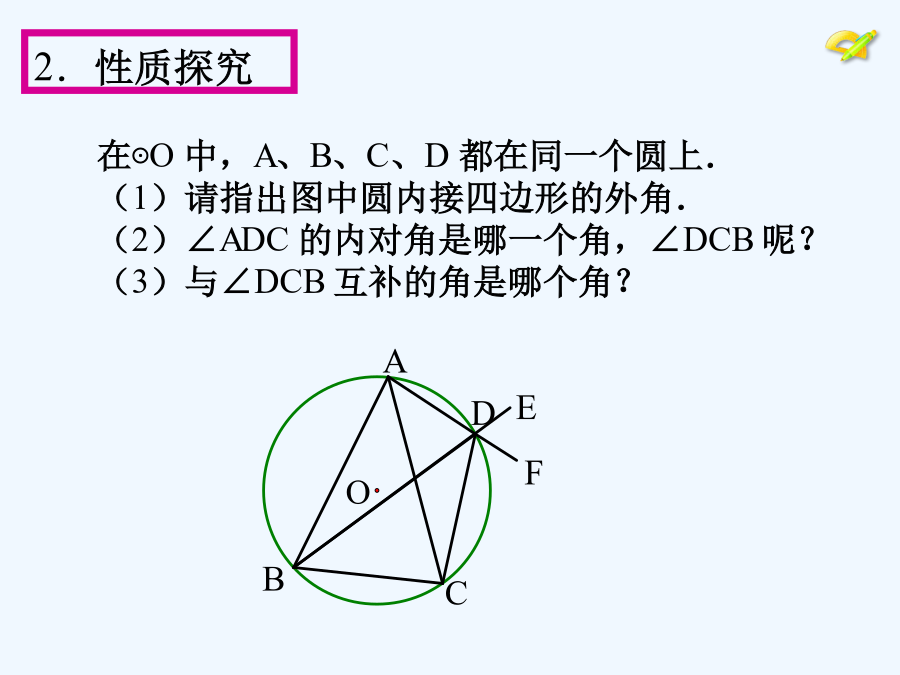
九年级上册圆内接四边形的性质是圆周角定理的应用.利用圆周角定理,可以把圆内接四边形的四个内角(圆周角)和相应的圆心角联系起来,得到圆内接四边形的性质.圆内接四边形的性质在圆中探究角相等或互补关系时经常用到,也是研究四点共圆的基础.学习目标:1.掌握圆内接四边形的概念和性质;2.会运用圆内接四边形的性质证明和计算一些问题.学习重点:圆内接四边形的概念和性质.什么叫圆内接三角形?什么叫圆内接四边形?观察圆内接四边形对角之间有什么关系.如何验证你的猜想呢?在⊙O中,A、B、C、D都在同一个圆上.(1)请指出图中

241 圆的有关性质(第5课时).ppt
九年级上册圆内接四边形的性质是圆周角定理的应用.利用圆周角定理,可以把圆内接四边形的四个内角(圆周角)和相应的圆心角联系起来,得到圆内接四边形的性质.圆内接四边形的性质在圆中探究角相等或互补关系时经常用到,也是研究四点共圆的基础.学习目标:1.掌握圆内接四边形的概念和性质;2.会运用圆内接四边形的性质证明和计算一些问题.学习重点:圆内接四边形的概念和性质.什么叫圆内接三角形?什么叫圆内接四边形?观察圆内接四边形对角之间有什么关系.如何验证你的猜想呢?在⊙O中,A、B、C、D都在同一个圆上.(1)请指出图中

241圆的有关性质(第5课时).ppt
九年级上册圆内接四边形的性质是圆周角定理的应用.利用圆周角定理,可以把圆内接四边形的四个内角(圆周角)和相应的圆心角联系起来,得到圆内接四边形的性质.圆内接四边形的性质在圆中探究角相等或互补关系时经常用到,也是研究四点共圆的基础.学习目标:1.掌握圆内接四边形的概念和性质;2.会运用圆内接四边形的性质证明和计算一些问题.学习重点:圆内接四边形的概念和性质.什么叫圆内接三角形?什么叫圆内接四边形?观察圆内接四边形对角之间有什么关系.如何验证你的猜想呢?在⊙O中,A、B、C、D都在同一个圆上.(1)请指出图中

241 圆的有关性质(第5课时).ppt
九年级上册圆内接四边形的性质是圆周角定理的应用.利用圆周角定理,可以把圆内接四边形的四个内角(圆周角)和相应的圆心角联系起来,得到圆内接四边形的性质.圆内接四边形的性质在圆中探究角相等或互补关系时经常用到,也是研究四点共圆的基础.学习目标:1.掌握圆内接四边形的概念和性质;2.会运用圆内接四边形的性质证明和计算一些问题.学习重点:圆内接四边形的概念和性质.什么叫圆内接三角形?什么叫圆内接四边形?观察圆内接四边形对角之间有什么关系.如何验证你的猜想呢?在⊙O中,A、B、C、D都在同一个圆上.(1)请指出图中

241 圆的有关性质(第5课时).ppt
九年级上册圆内接四边形的性质是圆周角定理的应用.利用圆周角定理,可以把圆内接四边形的四个内角(圆周角)和相应的圆心角联系起来,得到圆内接四边形的性质.圆内接四边形的性质在圆中探究角相等或互补关系时经常用到,也是研究四点共圆的基础.学习目标:1.掌握圆内接四边形的概念和性质;2.会运用圆内接四边形的性质证明和计算一些问题.学习重点:圆内接四边形的概念和性质.什么叫圆内接三角形?什么叫圆内接四边形?观察圆内接四边形对角之间有什么关系.如何验证你的猜想呢?在⊙O中,A、B、C、D都在同一个圆上.(1)请指出图中
