非线性本构关系简介.pptx

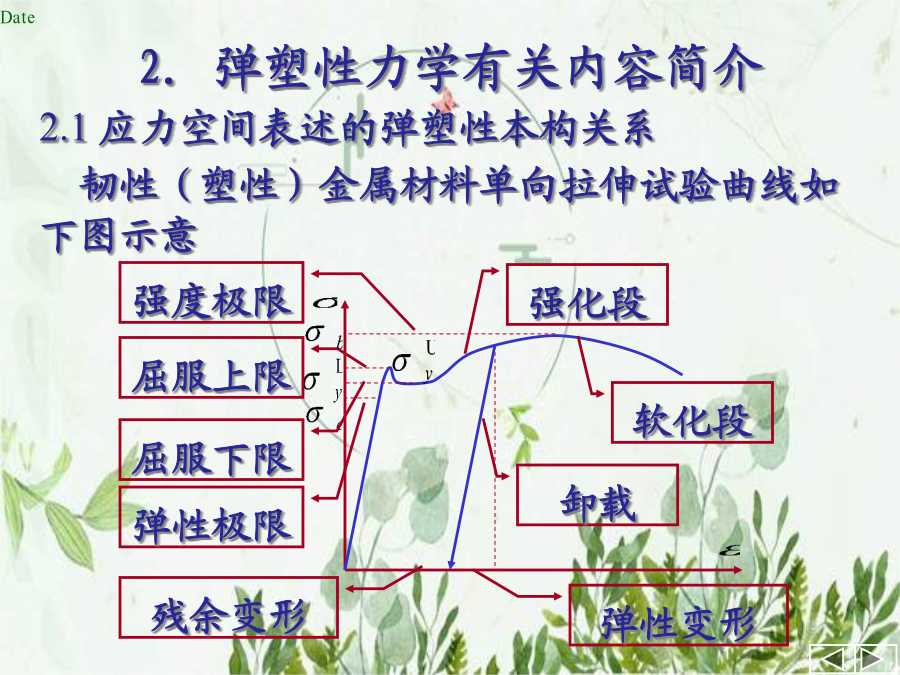
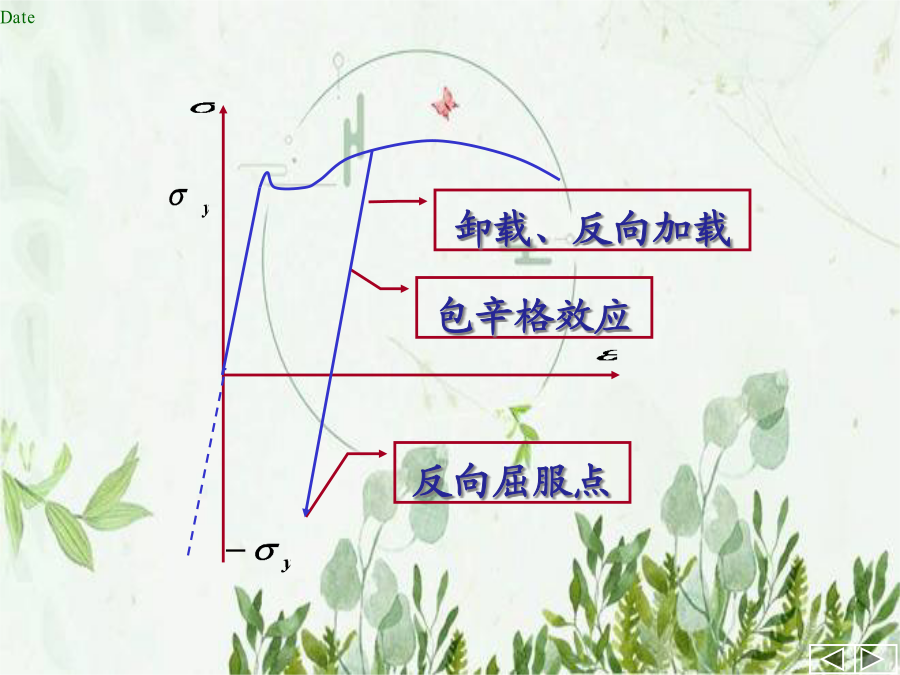
非线性本构关系简介.ppt1.弹性介质本构关系式中应力和应变偏张量分别为利用上述关系，只要已知两个弹性常数就可写出有限元分析中的弹性矩阵(D)。非线性弹性介质的本构关系，一般是根据材料的力学试验通过拟合来得到的。例如金属材料单向拉伸Romberg-Osgood模型的关系为全量本构关系的表达形式和线性弹性情况相同，也即韧性（塑性）金属材料单向拉伸试验曲线如下图示意包辛格效应由单向拉伸曲线可见，弹塑性材料受外部作用的反应和变形的历史有关（可称为历史相关性或路径相关性），因此本构关系应写成增量关系。又因弹塑性状态下加载和卸载有不同的规律，所以其本构关系的表述要比非线性弹性情况复杂。屈服条件曾经有最大主应力（伽）、最大主应变（圣）假设，但后来都被实验所否定。在材料的一般应力状态下，可认为应力满足如下条件时材料发生屈服，即处于塑性状态：从自然状态第一次进入屈服的屈服条件称初始屈服条件，产生塑性变形后的屈服条件称后继屈服条件。初始屈服条件可表为：，它只与当前应力状态有关。屈服条件都可看成应力空间的超曲面，初始屈服条件称初始屈服面，后继屈服条件称后继屈服面，统称屈服面。等向强化等向强化认为屈服面形状不变，只是作均匀的扩张，后继屈服面仅与一个和内变量有关的参数有关，可表为：2）塑性状态的加载和卸载准则2-2)具有强化的弹塑性材料3）流动准则4）弹塑性本构关系对于具有强化的加载状态，因为屈服面为由此可见，只要建立了屈服面方程，则对应加载状态应力增量dσij的应变增量dεij为必须注意，这里导数是由应力空间屈服面定义的，但是它是应变空间表述的。位移有限元分析用它！