
轴向拉伸和压缩.ppt

明轩****la







亲,该文档总共85页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

轴向拉伸和压缩.doc
轴向拉伸和压缩、剪切1.横截面面积A=10cm2的钢杆,其两端固定,受载情况如图所示,P=100kN。试求钢杆各段的应力。P400mmIII400mm2.图示阶梯形杆,材料为钢,其E钢=200GN/m2,两段的横截面积不同,上段A上=2cm2,下段A下=4cm2,两段的长度相等,l=50cm,受载荷P=60kN的作用,求各段的应力。llP3.图示结构,AB杆材料为钢,其[]钢=160MN/m2,BC杆材料为木材,其[]木=8MN/m2。AB杆为5号槽钢,由表查得其截面面

轴向拉伸和压缩.ppt
第二章轴向拉伸和压缩§2–1轴向拉压的概念轴向压缩,对应的力称为压力。一、内力指由外力作用所引起的、物体内相邻部分之间分布内力系的合成(附加内力)。二、截面法·轴力2.轴力——轴向拉压杆的内力,用N表示。①反映出轴力与截面位置变化关系,较直观;②确定出最大轴力的数值及其所在横截面的位置,即确定危险截面位置,为强度计算提供依据。[例1]图示杆的A、B、C、D点分别作用着大小为5P、8P、4P、P的力,方向如图,试画出杆的轴力图。同理,求得AB、BC、CD段内力分别为:轴力(图)的简便求法:自左向右:解:x坐

轴向拉伸和压缩.ppt
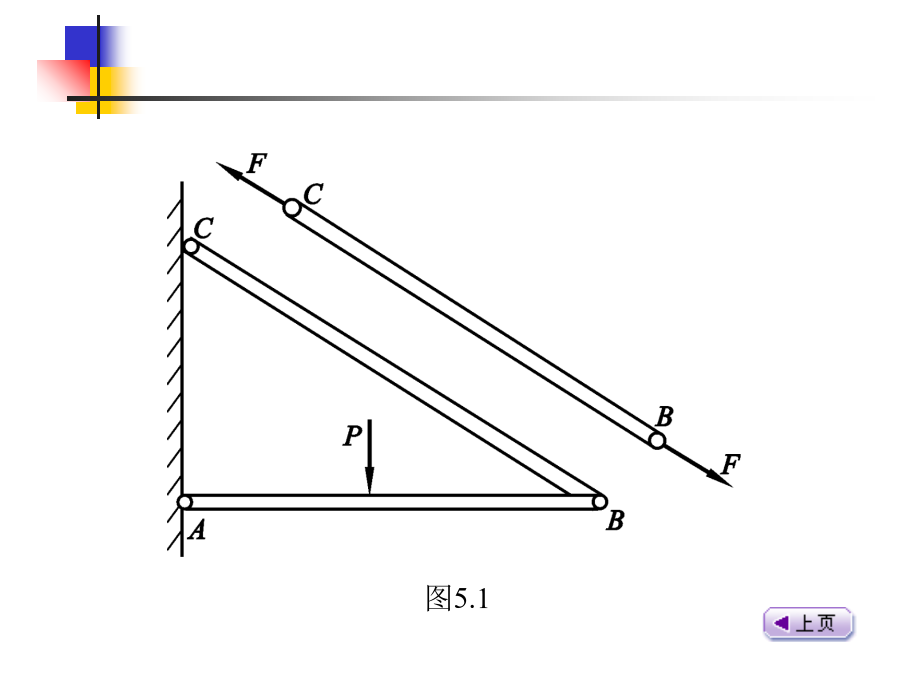
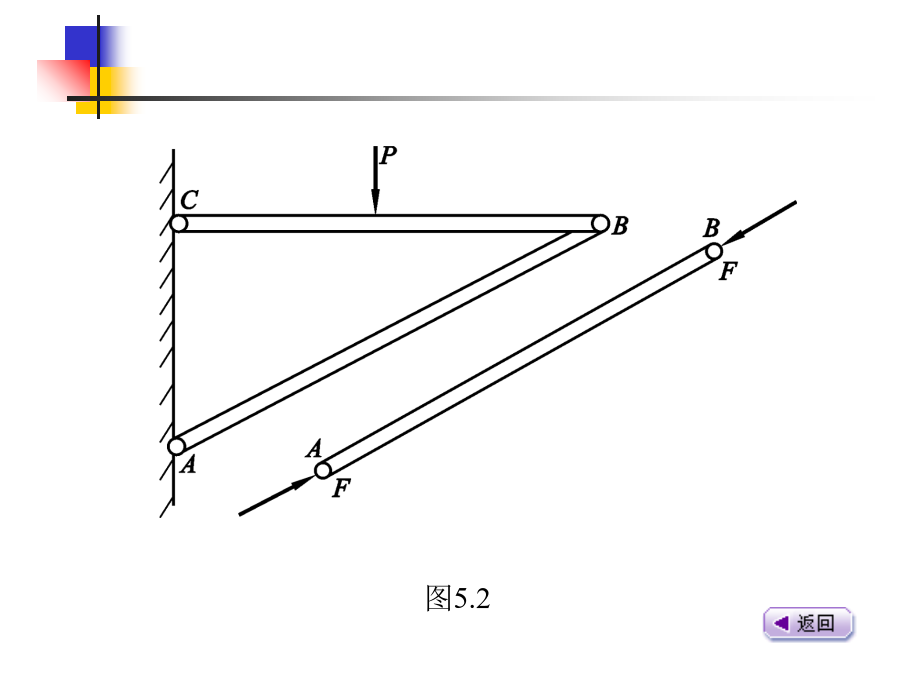
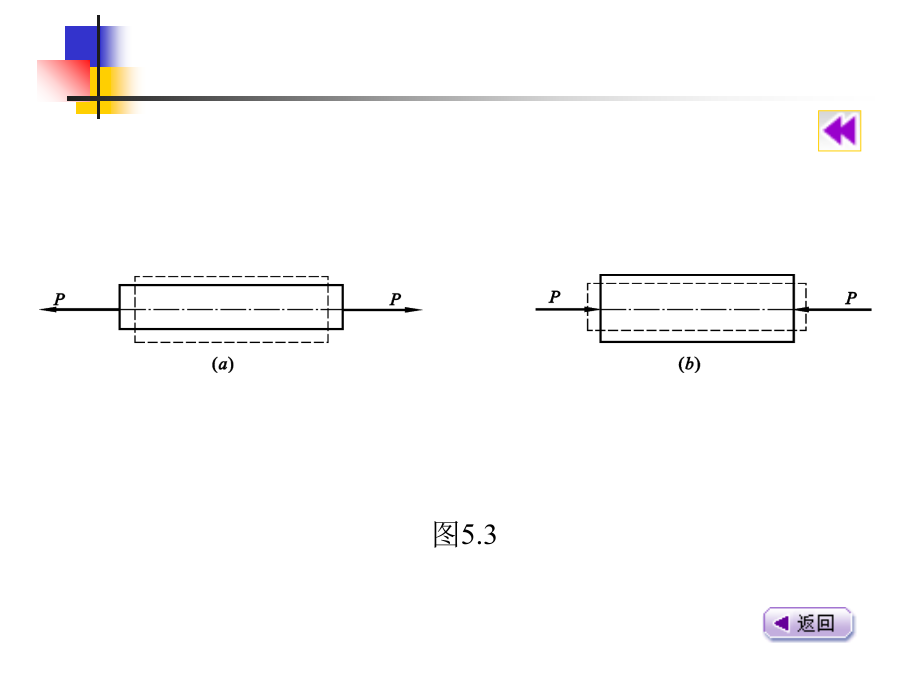
5轴向拉伸和压缩本章内容5.1轴向拉伸和压缩的概念图5.1图5.2图5.35.2轴向拉伸和压缩时的内力【例5.1】杆件受力如图5.5(a)所示,试分别求出1-1、2-2、3-3截面上的轴力。【解】(1)计算1-1截面的轴力假想将杆沿1-1截面截开,取左端为研究对象,截面上的轴力N1按正方向假设,受力图如图5.5(b)所示。由平衡方程∑Fx=0,N1-P=0N1=P(拉力)(2)计算2-2截面的轴力假想将杆沿2-2截面截开,取左端为研究对象,截面上的轴力N2按正方向假设,受力图如图5.5(c

轴向拉伸和压缩.ppt
5轴向拉伸和压缩本章内容5.1轴向拉伸和压缩的概念图5.1图5.2图5.35.2轴向拉伸和压缩时的内力【例5.1】杆件受力如图5.5(a)所示,试分别求出1-1、2-2、3-3截面上的轴力。【解】(1)计算1-1截面的轴力假想将杆沿1-1截面截开,取左端为研究对象,截面上的轴力N1按正方向假设,受力图如图5.5(b)所示。由平衡方程∑Fx=0,N1-P=0N1=P(拉力)(2)计算2-2截面的轴力假想将杆沿2-2截面截开,取左端为研究对象,截面上的轴力N2按正方向假设,受力图如图5.5(c

轴向拉伸和压缩.docx
课题序号授课班级授课课时2授课形式复习授课章节名称轴向拉伸和压缩的内力及应力使用教具教学目的1、了解轴向拉伸和压缩的概念;2、掌握截面法求轴力和应力;3、正确画出轴力图.教学重点轴力图的画法.教学难点截面法求解轴力和应力.更新、补充、删节内容课外作业教学后记教学过程了解掌握1.强度、刚度、稳定性的概念;材料力学的研究对象;2.轴向拉伸和压缩的概念。1.用截面法求轴向拉、压杆横截面上的轴力、应力,画轴力图;2.虎克定律,杆件轴向变形的计算和线应变的概念;3.轴向拉、压杆的强度计算。2011年2012年201
