
固体物理导论1.9省名师优质课赛课获奖课件市赛课一等奖课件.ppt

赫赫****等你







亲,该文档总共13页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

固体物理导论1.9省名师优质课赛课获奖课件市赛课一等奖课件.ppt
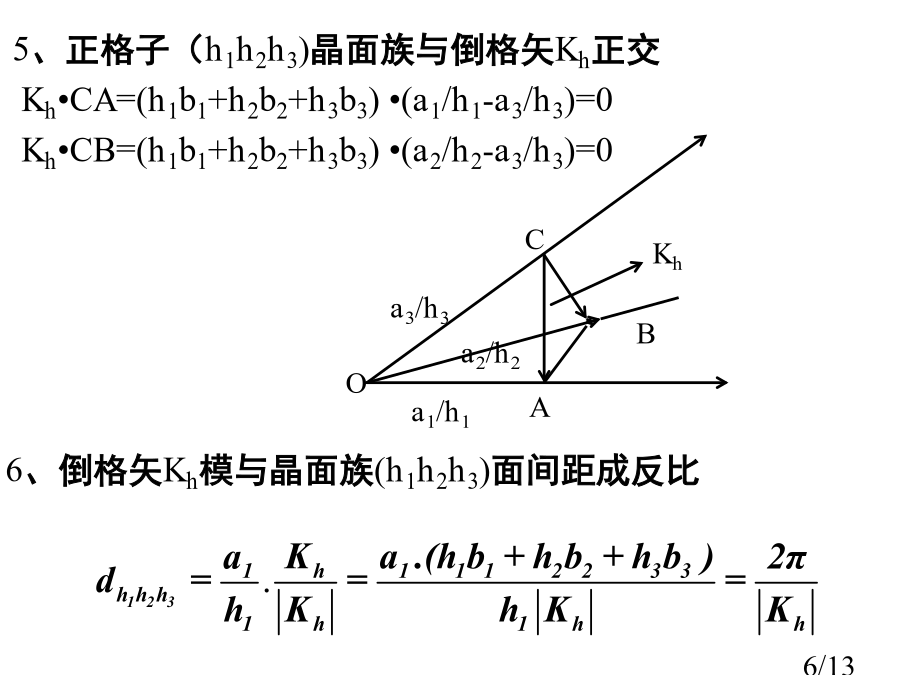
第九节倒格子2、倒格子布拉维格子基矢a1、a2、a3为正格子基矢,称Rl=l1a1+l2a2+l3a3决定空间为正格子,=a1·(a2×a3)为正格子原胞体积。定义为倒格子基矢,由Kh=h1b1+h2b2+h3b3决定空间为倒格子,=b1·(b2×b3)为倒格子原胞体积。正格子空间长度量纲是m,倒格子空间长度量纲为m-1。3、倒格子意义正格子中一族晶面转化成了倒格子中一个倒格点。(1)由和叉乘几何意义可知,b3沿着a1×a2方向,或者说b3就是a1和a2所确定晶面(001)法线方向。同时倒格子基矢b

固体物理-2省名师优质课赛课获奖课件市赛课一等奖课件.ppt
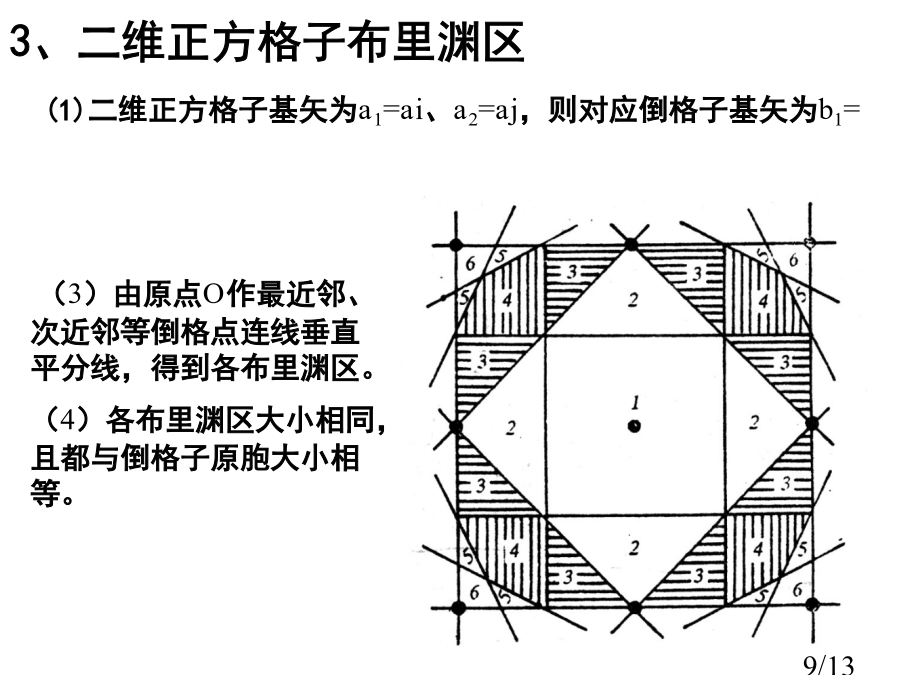
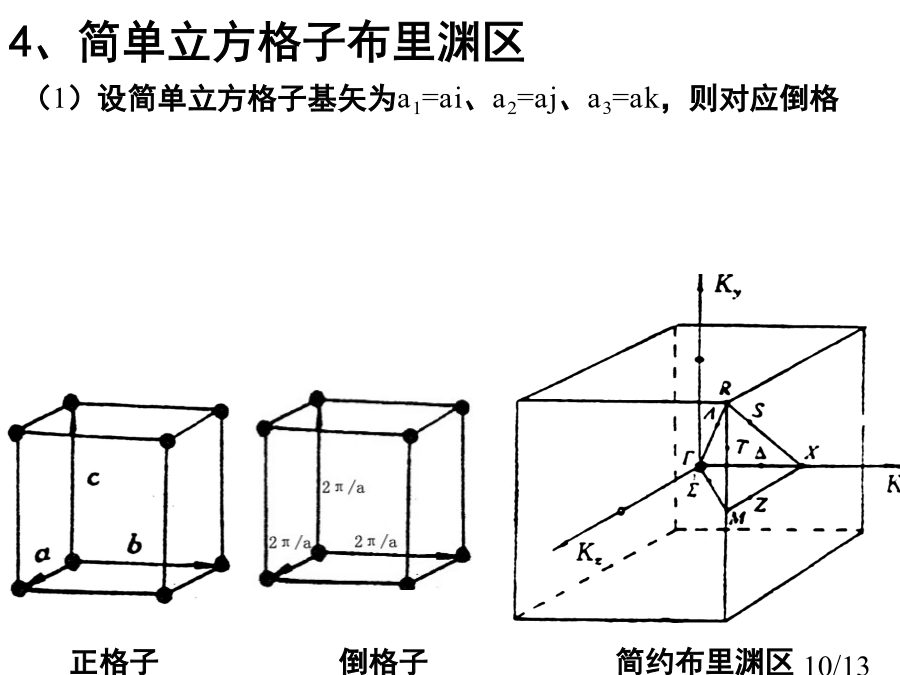
材料物理基础倒格子研究倒易点阵意义倒格子引入几何关系直观观察一、倒格子定义从数学上讲,倒易点阵和布喇菲点阵是相互对应傅里叶空间。例1:简立方格子倒格子。二、倒格子基矢性质倒格矢与正格子晶面关系推论:三、结晶学中倒格子(晶胞)倒格矢性质:例题选做例三:晶格周期函数傅里叶展开(掌握思绪)所以V(1,23)可展成傅里叶级数傅里叶级数可直接用r表示出来,即布里渊区布里渊区性质体心立方晶格第一布里渊区确定晶格参数方法——衍射条件确定晶格参数方法——三种主要衍射伎俩确定晶格参数方法——确定衍射极大位置确定晶格参

固体物理学-5省名师优质课赛课获奖课件市赛课一等奖课件.ppt
点缺点晶体中原子扩散线缺点—位错面缺点离子晶体中缺点和离子性导电完美晶体:全部原子或离子都排列在晶格中它们自己位置上,没有外来杂质;晶体原子之比符合化学计量比。实际晶体:与理想晶体有一些差异。或多或少地存在这么那样缺点。晶体缺点存在,破坏了完美晶体有序性,引发晶体内能U和熵S增加。按缺点在空间几何构型可将缺点分为点缺点、线缺点、面缺点和体缺点,它们分别取决于缺点延伸范围是零维、一维、二维还是三维。每一类缺点都会对晶体性能产生很大影响,比如点缺点会影响晶体电学、光学和机械性能,线缺点会严重影响晶体强度、电性

固体物理黄昆一省名师优质课赛课获奖课件市赛课一等奖课件.ppt
为学之道,莫先于穷理;穷理之要,必在于读书;读书之法,莫贵于循序而致精;而致精之本,则又在于居敬而持志。——朱熹主要参考书一、固体物理学研究对象固体分类规则网络准晶二、固体物理学发展历史二、学科领域本课程学习内容第一章晶体结构晶体宏观性质周期性--从原子排列角度来讲(均一性――从宏观理化性质角度来讲);宏观对称性;3.各向异性和解理性。比如,云母解理性;4.有固定熔点。几个常见晶体结构a.较涣散堆积面心立方(face-centeredcubic,fcc)堆积排列方式:ABCABC(立方密堆积)

《蒹葭》获奖省名师优质课赛课获奖课件市赛课一等奖课件.ppt
蒹葭学习目标解题在水一方一、听读:感受诗音乐美蒹葭苍苍,白露为霜。所谓伊人,在水一方。溯洄从之,道阻且长;溯游从之,宛在水中央。蒹葭萋萋,白露未晞。所谓伊人,在水之湄。溯洄从之,道阻且跻;溯游从之,宛在水中坻。蒹葭采采,白露未已,所谓伊人,在水之涘。溯洄从之,道阻且右;溯游从之,宛在水中沚。检验字词掌握情况。朗诵课文,疏通文意。蒹葭/苍苍,白露/为霜。所谓/伊人,在水/一方。溯洄/从之,道阻/且长。溯游/从之,宛在/水中央。蒹葭/萋萋,白露/未晞。所谓/伊人,在水/之湄。溯洄/从之,道阻/且跻。溯游/从之
