信号分析与处理技术习题册.pdf

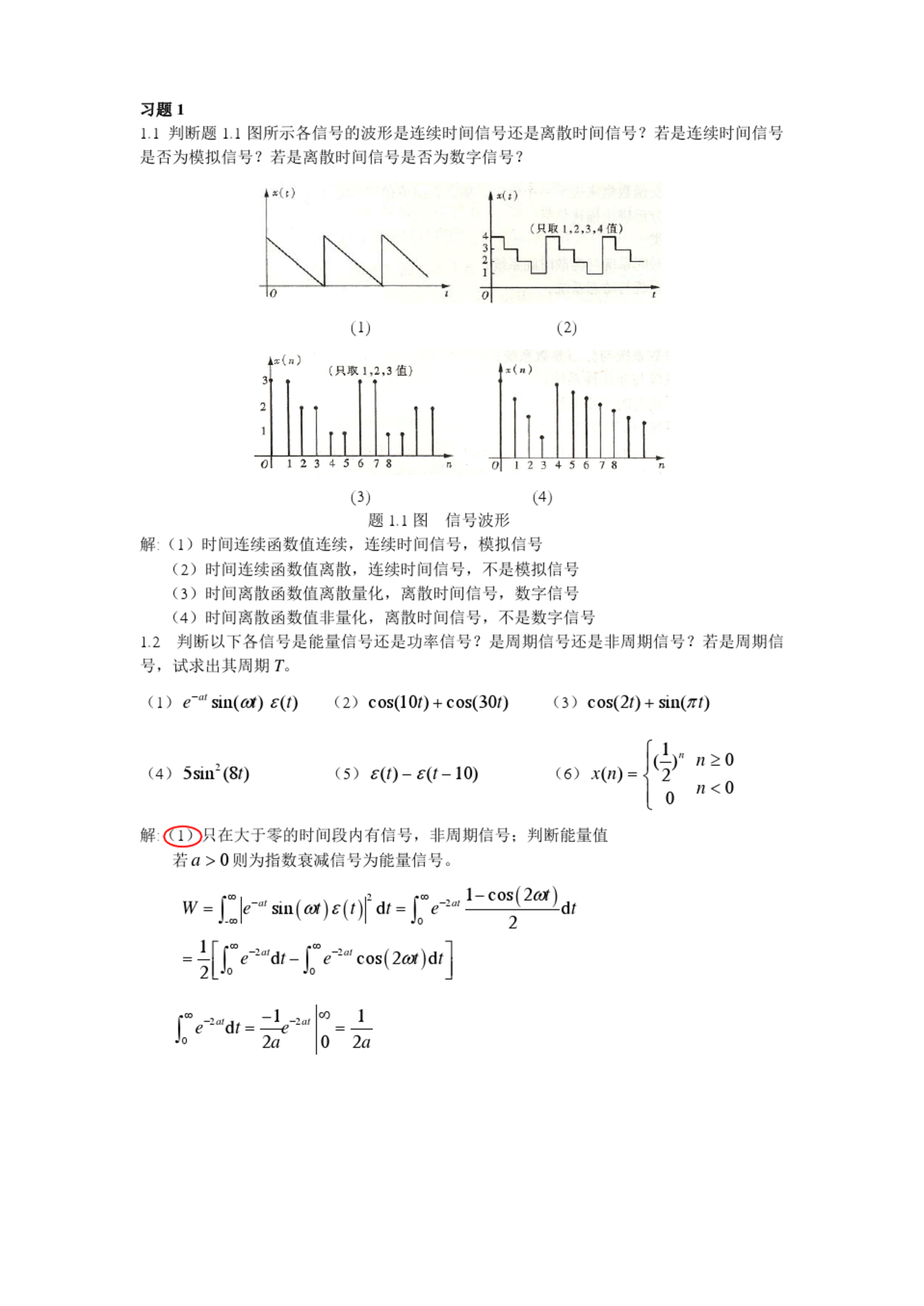
第一章时域离散信号与离散系统1－1给定信号：2n5,4n1x(n)6,0n40,其它（1）画出x(n)序列的波形，标上各序列值；（2）试用延迟的单位脉冲序列及其加权和表示x(n)序列；（3）令x(n)=2x(n-2),试画出x(n)波形；11（4）令x(n)=2x(n+2)，试画出x(n)波形；22（5）令x(n)=x(2-n)，试画出x(n)波形。331－2有序列如下图所示请计算x(n)=[x(n)+x(-n)]/2，并画出波形。e1－3试判断n（1）y(n)x(m)m（2）y(n)=[x(n)]22（3）y(n)x(n)sin(n)97是否线性系统，并判断（2）、（3）是否移不变系统。1－4设线性时不变系统的单位脉冲响应h(n)和输入序列x(n)如图所示，要求画出y(n)的波形。1－5已知线性移不变系统的输入为x(n)=(n)-(n-2),系统的单位抽样响应为h(n)=0.5nR(n)，试求系统的输出y(n)31－6设有一系统，其输入输出关系由以下差分方程确定：y(n)-0.5y(n-1)=x(n)+0.5x(n-1)设系统是因果性的。（1）利用递推法求系统的单位抽样响应；（2）由（1）的结果，利用卷积和求输入x(n)=ejwnu(n)的响应。第二章时域离散信号与系统的频域分析2－1试求如下序列的傅立叶变换：（1）x(n)=R(n)15（2）x(n)=u(n+3)-u(n-4)22－2设1,n0,1，将x(n)以4为周期进行周期延拓，形成周期x(n)0,其它~~~~序列x(n)，画出x(n)和x(n)的波形，求出x(n)的离散傅立叶级数X(k)和傅立叶变换。2－3设如图所示的序列x(n)的FT用X(ejw)表示，不直接求出X(ejw)，确定并画出傅立叶变换实部Re[X(ejw)]的时间序列x(n)e2－4求序列-2-nu(-n-1)的Z变换及收敛域：3z12－5已知X(z)，求收敛0.5|z|2对应的原序列x(n)25z12z22－6分别用长除法、部分分式法求以下X(z)的反变换：11z131X(z),|z|121z242－7用Z变换法解下列差分方程：y(n)-0.9y(n-1)=0.05u(n),y(-1)=1,y(n)=0,n<-12－8研究一个输入为x(n)和输出为y(n)的时域线性离散移不变系10统，已知它满足y(n1)y(n)y(n1)x(n)，并已知系统是稳定的，3试求其单位抽样响应。第三章离散傅立叶变换（DFT）3－1计算以下序列的N点DFT，在变换区间0≤n≤N-1内，序列的定义为x(n)=sin(wn)·R(n)0NNej,km2N3－2已知X(k)ej,kNm，求x(n)=IDFT[X(k)]20,其它k3－3长度为N＝10的两个有限长序列1,0n4x(n)10,5n91,0n4x(n)21,5n9作图表示x(n)、x(n)和y(n)=x(n)③x(n)12123－4在图中画了两个有限长序列，试画出它们的六点圆周卷积。3－5若X(k)=DFT[x(n)]，Y(k)=DFT[y(n)]，Y(k)=X((k+l))·R(k)，证NN明y(n)=IDFT[Y(k)]=Wlnx(n)N3－6已知有限长序列x(n)，0≤n≤N-1，现重复序列x(n)产生一个rN点的h(n)，求h(n)的DFT值H(k)，解释其结果的意义。第四章快速傅立叶变换（FFT）4－1如果一台通用计算机的速度为：平均每次复乘需100us，每次复加需20us，用来计算N=1024的DFT，问直接运算需要多少时间？用FFT运算需要多少时间？4－2作16点DIT-FFT运算流图第五章时域离散系统的基本网络结构与状态变量分析法5－1设系统用下面差分方程描述：311y(n)y(n1)y(n2)x(n)x(n1)483试画出系统的直接型、级联型和并联型结构。5－2已知滤波器的单位脉冲响应为h(n)=0.9nR(n)，求出系统函数，5并画出其直接型结构。第六章无限脉冲响应数字滤波器的设计6－1设计一个巴特沃斯低通滤波器，要求通带截止频率f=6kHz，p通带最大衰减=3dB，阻带截止频率f=12kHz，阻带最小衰减ps=25dB。求出滤波器归一化传输函数H(p)以及实际的H(s)。saa6－2已知模拟滤波器的传输函数H(s)为：ab，式中，a,b为常数，设H(s)因果稳定，试采用脉H(s)aa(sa)2b2冲响应不变法，分别将其转换成数字滤波器H(z)。6－3设计低通数字滤波器，要求通带内频率低于0.2rad时，容许幅度误差在1dB之内；频率在0.3到之间的阻带衰减大