勾股定理（二）勾股定理的应用.pptx

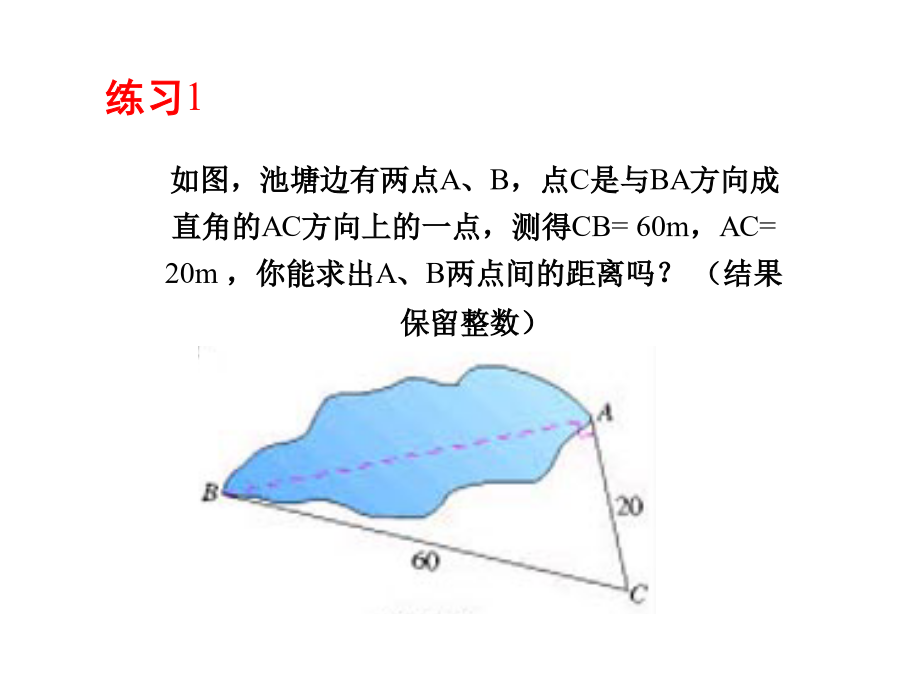
历史因你而改变学习因你而精彩如图，受台风“麦莎”影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？1.经历探索勾股定理的过程，会应用勾股定理进行简单的计算。
2.能从实际问题中抽象出直角三角形这一几何模型，会用勾股定理解决实际问题。
第二步：自学自研（独学）合学第三步：交流展示[（A）展（B）板]例1
练习1两千多年前，古希腊有个哥拉勾股史话在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.毕达哥拉斯定理：1、在直角三角形ABC中，∠C=900，∠A、∠B、∠C所对的边分别为a、b、c
（1）已知a=1，b=2，求c
（2）已知a=10，c=15，求b2、下列说法正确的是（）
A.若a、b、c是△ABC的三边，则:
B.若a、b、c是Rt△ABC的三边，则
C.若a、b、c是Rt△ABC的三边，，则

D.若a、b、c是Rt△ABC的三边，，则3、一个直角三角形中，两直角边长分别为3和4，下列说法正确的是（）
A．斜边长为25B．三角形周长为25
C．斜边长为5D．三角形面积为20
4、如图,三个正方形中,S1＝25，S2＝144，则另一个的面积S3为________．

5、一个直角三角形的两边长分别为5cm和12cm,则第三边的长为。第五步：学教反思作业祝同学们学习进步！