垂径定理习题课.ppt

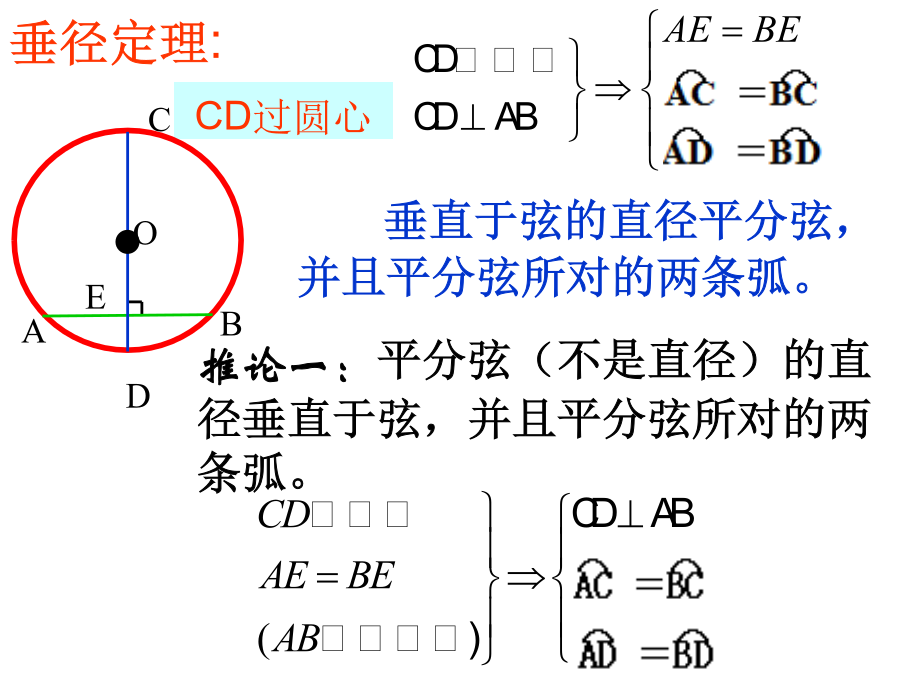
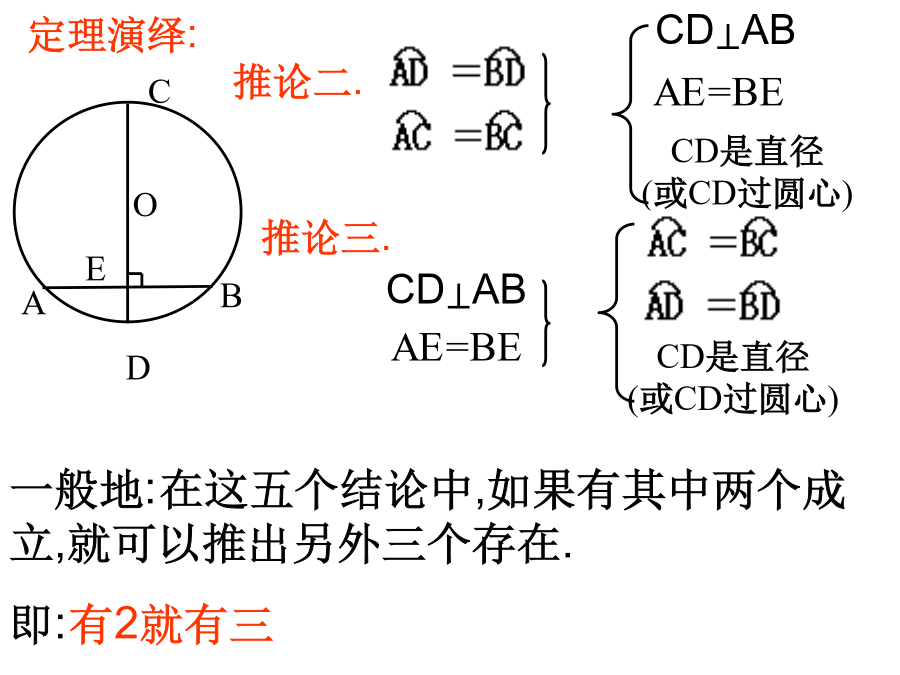
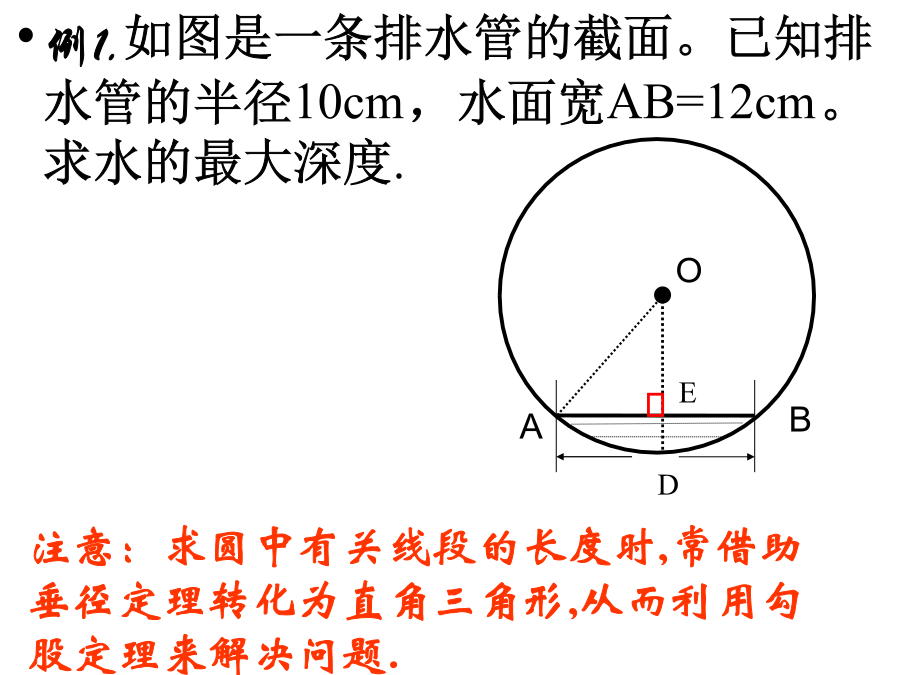
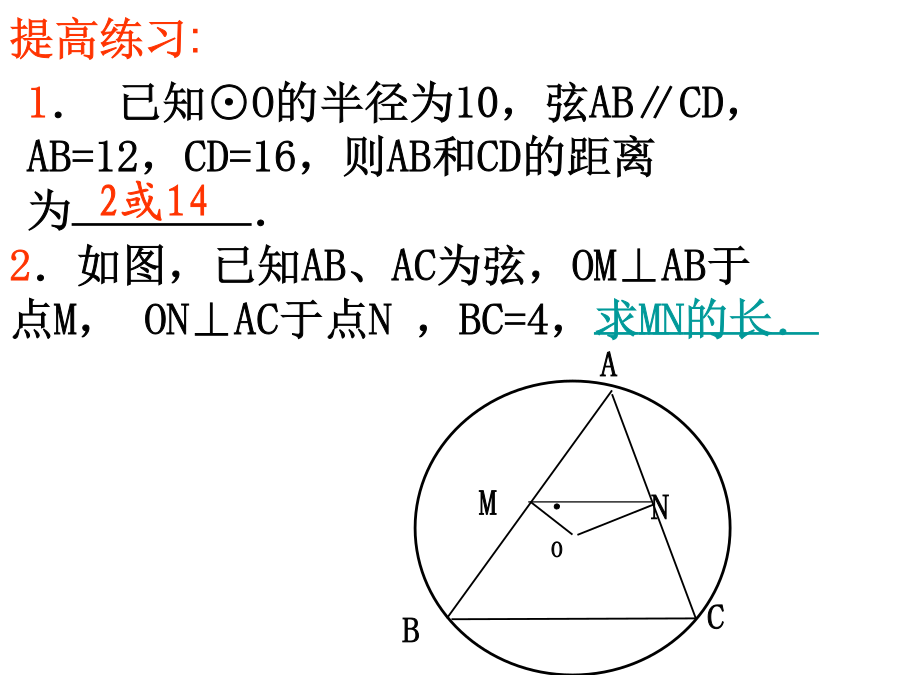
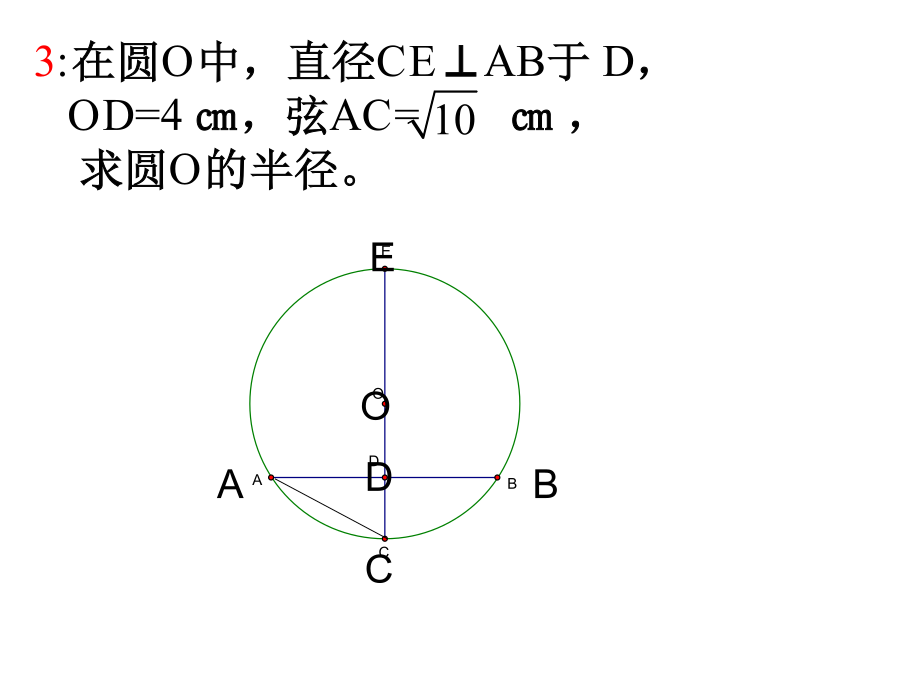
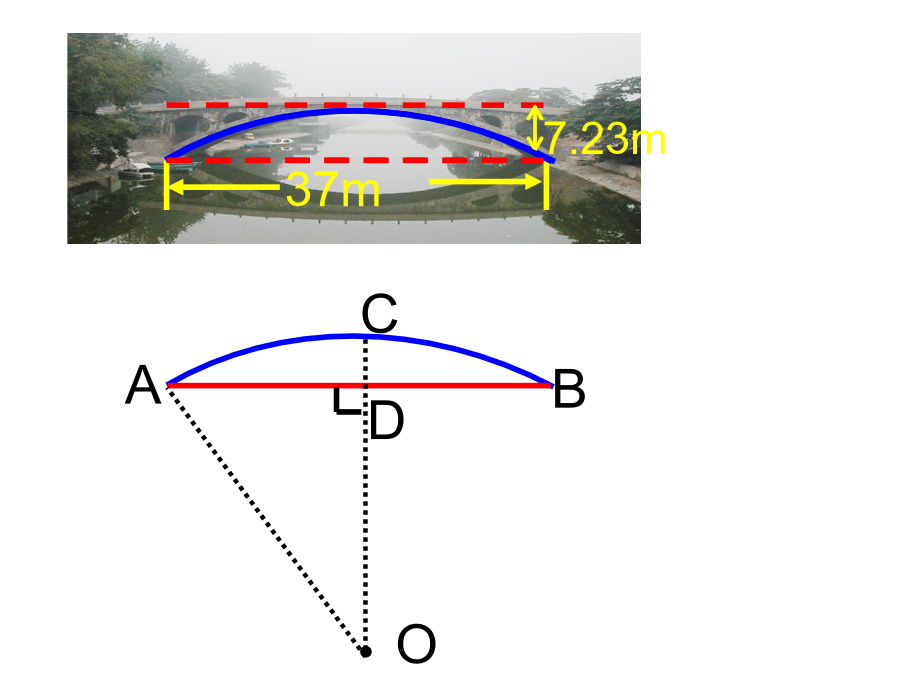
垂径定理习题课垂直于弦的直径平分弦，并且平分弦所对的两条弧。定理演绎:试一试例1.如图是一条排水管的截面。已知排水管的半径10cm，水面宽AB=12cm。求水的最大深度.练习1:如图，CD为圆O的直径，弦AB交CD于E，∠CEB=30°，DE=9㎝，CE=3㎝，求弦AB的长。1．已知⊙O的半径为10，弦AB∥CD，AB=12，CD=16，则AB和CD的距离为．3:在圆O中，直径CE⊥AB于D，OD=4㎝，弦AC=㎝，求圆O的半径。例2：你知道赵州桥吗?它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m，你能求出赵州桥主桥拱的半径吗？解得：R≈27．3（m）课堂小结:1、如图，在⊙O中，CD是直径，AB是弦，且CD⊥AB，已知CD=20，CM=4，则AB=_________2.已知:如图,AB,CD是⊙O直径,D是弧AE中点,AE与CD交于F,OF=3,则BE=.2.如图，CD垂直平分AB，若已知AD=，CD=2,这个圆的半径是.如图，弓形ABC中，弦AC的长为8厘米，弦的中点到劣弧中点间的长度是2厘米，则圆的半径=_________弓形的弦长为8cm，弓形的高2cm，则这弓形所在的圆的半径为.根据垂径定理与推论可知：对于一个圆和一条直线来说，如果具备：.如图,⊙O直径AB和弦CD相交于点E,已知AE=6cm,BE=2cm,∠CEA=30°,则CD长为.1.已知:如图,⊙0直径是8cm,C是弧AB中点,弦AB,CD相交于P,CD=cm求∠APC的度数2.已知:如图,⊙O半径OA=1,弦AB,AC的长分别是求∠BAC的度数已知:⊙O半径OA=1,弦AB,AC的长分别是求∠BAC的度数如图，已知⊙O的半径长为25，弦AB长为48，C是弧AB的中点．求AC的长．变式练习：已知⊙O的半径长为25，弦AB长为48，C是弦AB所对的弧的中点．求AC的长．有一石拱桥的桥拱是圆弧形，如下图所示，正常水位下水面宽AB=60米，水面到拱顶距离CD=18米，当洪水泛滥，水面宽MN=32米时，高度为5m的船是否能通过该桥，请说明理由．练习2解：如图，用半圆O表示通道上面的半圆，AB为直径，弦CD平行AB，过O作于E，连结OD，据垂径定理知：2.某地方有座弧形的拱桥，如图，桥下的水面宽为7.2米，拱顶高出水面2.4米，现有一艘宽3米，船舱顶部为长方形并高出水面2米的货船要经过这里，此货船能顺利通过这座拱形桥吗？挖掘潜力练习（1）第一方案：设抛物线的表达式是y=a（x+6）（x-6）把C（0，4）代入得a=-1/9．∴y=-1/9x²+4．当y=3时得3=-1/9t²+4∴t=3∴当高度是3m时，最大宽度是6m．3.由于过度地采伐森林和破坏植被，使我国许多地区频频遭受沙尘暴的侵袭．近日A市气象局测得沙尘暴中心在A市的正西方向300km的B处，正以课堂小结: