高考数学 基本初等函数(Ⅱ)总复习课件.ppt

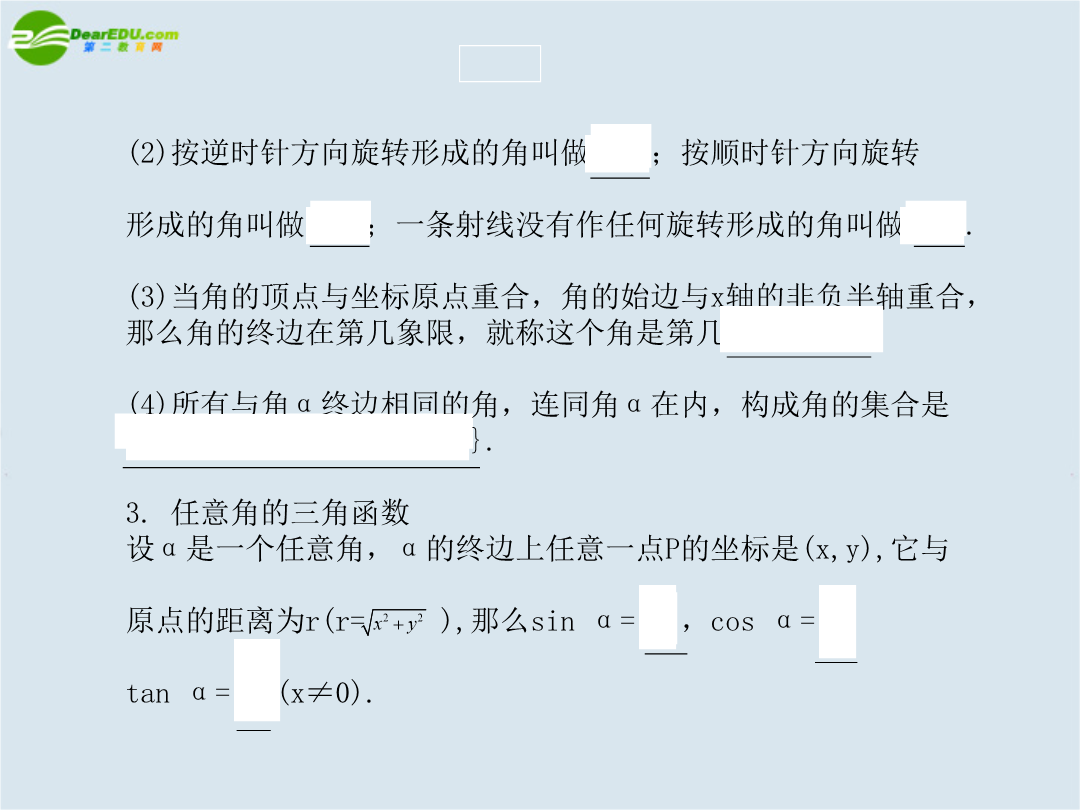
数学直通车之---基本初等函数（Ⅱ）第一节任意角与弧度制及任意角的三角函数(2)按逆时针方向旋转形成的角叫做正角；按顺时针方向旋转形成的角叫做负角；一条射线没有作任何旋转形成的角叫做零角.(3)当角的顶点与坐标原点重合角的始边与x轴的非负半轴重合那么角的终边在第几象限就称这个角是第几象限角.(4)所有与角α终边相同的角连同角α在内构成角的集合是{β|β=k·360°+αk∈Z}.3.任意角的三角函数设α是一个任意角α的终边上任意一点P的坐标是(xy)它与原点的距离为r(r=)那么sinα=cosα=tanα=(x≠0).4.单位圆与三角函数线用单位圆中的有向线段表示三角函数（如图）.典例分析分析由于α是第二象限的角可以利用终边相同的角的表达式表示出α的范围进而求得2α的范围判定其所在的象限.（2）·360°+30°＜＜·360°+60°（k∈Z）①当k=3n（n∈Z时）n·360°+30°＜＜n·360°+60°（n∈Z）则是第一象限角;②当k=3n+1（n∈Z）时n·360°+150°＜＜n·360°+180°（n∈Z）则是第二象限角；③当k=3n+2（n∈Z）时n·360°+270°＜＜n·360°+300°（n∈Z）则是第四象限角.综合①、②、③可知是第一、第二或第四象限角.（3）2k·360°+180°＜2α＜2k·360°+360°（k∈Z）.故2α是第三、第四象限角或是终边落在y轴的负半轴上.解析:∵θ为第三象限角∴2kπ+π＜θ＜2kπ+(k∈Z)kπ+＜＜kπ+(k∈Z).当k=2n(n∈Z)时2nπ+＜＜2nπ+（n∈Z）此时在第二象限∴sin＞0cos＜0∴＜0；当k=2n+1(n∈Z)时(2n+1)π+＜＜(2n+1)π+(n∈Z)即2nπ+＜＜2nπ+(n∈Z)此时在第四象限∴sin＜0cos＞0∴＜0.综上可知:＜0.题型二扇形弧长、面积公式的应用举一反三(2)方法一：∵扇形周长C=2r+l=2r+αr∴r=∴=∴当且仅当α=即α=2(α=-2舍去)时扇形面积有最大值.方法二：由已知2r+l=C∴r=(l＜C)∴S==∴当l=时此时α=∴当扇形圆心角为2弧度时扇形面积有最大值.题型三利用三角函数的定义求三角函数值学后反思（1）当角α的终边上点的坐标以参数形式给出时要根据问题的实际及解题的需要对参数进行分类讨论.（2）熟记几组常用的勾股数组如(345)(51213)(72425)(81517)(94041)等会给我们解题带来很多方便.（3）若角α已经给定不论点P选择在α的终边上的什么位置角α的三角函数值都是确定的；另一方面如果角α终边上一点坐标已经确定那么根据三角函数定义角α的三角函数值也都是确定的.解析：当m＞0时点P在第二象限|OP|=5m有2sinα+cosα=当m＜0时点P在第四象限|OP|=-5m有2sinα+cosα=题型四利用三角函数线解三角不等式解(1)作直线y=交单位圆于A、B两点连接OA、OB则OA与OB围成的区域（图1中阴影部分）即为角α终边的范围.故满足条件的角α的集合为{α|2kπ+≤α≤2kπ+k∈Z}.(2)作直线x=-交单位圆于CD两点连接OC与OD则OC与OD围成的区域（图2中阴影部分）即为角α终边的范围.故满足条件的角α集合为{α|2kπ+≤α≤2kπ+k∈Z}..易错警示错解分析上述解题过程分别求出α、β的范围所采用的做法是不等价的扩大了范围.考点演练（2）当角α终边在第四象限时取点（1-3）此时x=1y=-3r=所以点C的坐标为（-2-23）点P走过的弧长为点Q走过的弧长为.第二节同角三角函数的基本关系与诱导公式即α+k·2π(k∈Z)-απ±α的三角函数值等于α的同名函数值前面加上一个把α看成锐角时原函数值的符号；±α的正弦（余弦）函数值分别等于α的余弦（正弦）函数值前面加上一个把α看成锐角时原函数值的符号.角α典例分析举一反三题型二同角三角函数关系的应用（二）【例2】已知.求sinx-cosx的值.学后反思如果已知sinα+cosαsinαcosαsinα-cosα中的一个完全可通过列方程（组）求出另外两个值.这里sinαcosα是纽带它把另外