
高考数学考前提分仿真试题(五)理 试题.doc

一只****生物










在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

高考数学考前提分仿真试题(五)理 试题.doc
2019届高考名校考前提分仿真卷理科数学(五)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答题前,考生务必将自己的姓名、考生号填写在答题卡上。2、回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。写在试卷上无效。3、回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。4、考试结束,将本试卷和答题卡一并交回。第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.

高考数学考前提分仿真试题(五)理 试题.doc
2019届高考名校考前提分仿真卷理科数学(五)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答题前考生务必将自己的姓名、考生号填写在答题卡上。2、回答第Ⅰ卷时选出每小题的答案后用铅笔把答题卡上对应题目的答案标号涂黑如需改动用橡皮擦干净后再选涂其他答案标号。写在试卷上无效。3、回答第Ⅱ卷时将答案填写在答题卡上写在试卷上无效。4、考试结束将本试卷和答题卡一并交回。第Ⅰ卷一、选择题:本大题共12小题每小题5分共60分.在每小题给出的四个选项中只有一项是符合题目要求的.1.[2019·合
高考数学考前提分仿真试题(一)理 试题.doc
2019届高考名校考前提分仿真卷理科数学(一)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答题前考生务必将自己的姓名、考生号填写在答题卡上。2、回答第Ⅰ卷时选出每小题的答案后用铅笔把答题卡上对应题目的答案标号涂黑如需改动用橡皮擦干净后再选涂其他答案标号。写在试卷上无效。3、回答第Ⅱ卷时将答案填写在答题卡上写在试卷上无效。4、考试结束将本试卷和答题卡一并交回。第Ⅰ卷一、选择题:本大题共12小题每小题5分共60分.在每小题给出的四个选项中只有一项是符合题目要求的.1.[2019·益

高考数学考前提分仿真试题(二)理 试题.doc
2019届高考名校考前提分仿真卷理科数学(二)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答题前考生务必将自己的姓名、考生号填写在答题卡上。2、回答第Ⅰ卷时选出每小题的答案后用铅笔把答题卡上对应题目的答案标号涂黑如需改动用橡皮擦干净后再选涂其他答案标号。写在试卷上无效。3、回答第Ⅱ卷时将答案填写在答题卡上写在试卷上无效。4、考试结束将本试卷和答题卡一并交回。第Ⅰ卷一、选择题:本大题共12小题每小题5分共60分.在每小题给出的四个选项中只有一项是符合题目要求的.1.[2019·韶

高考数学考前提分仿真试题(一)理 试题.doc
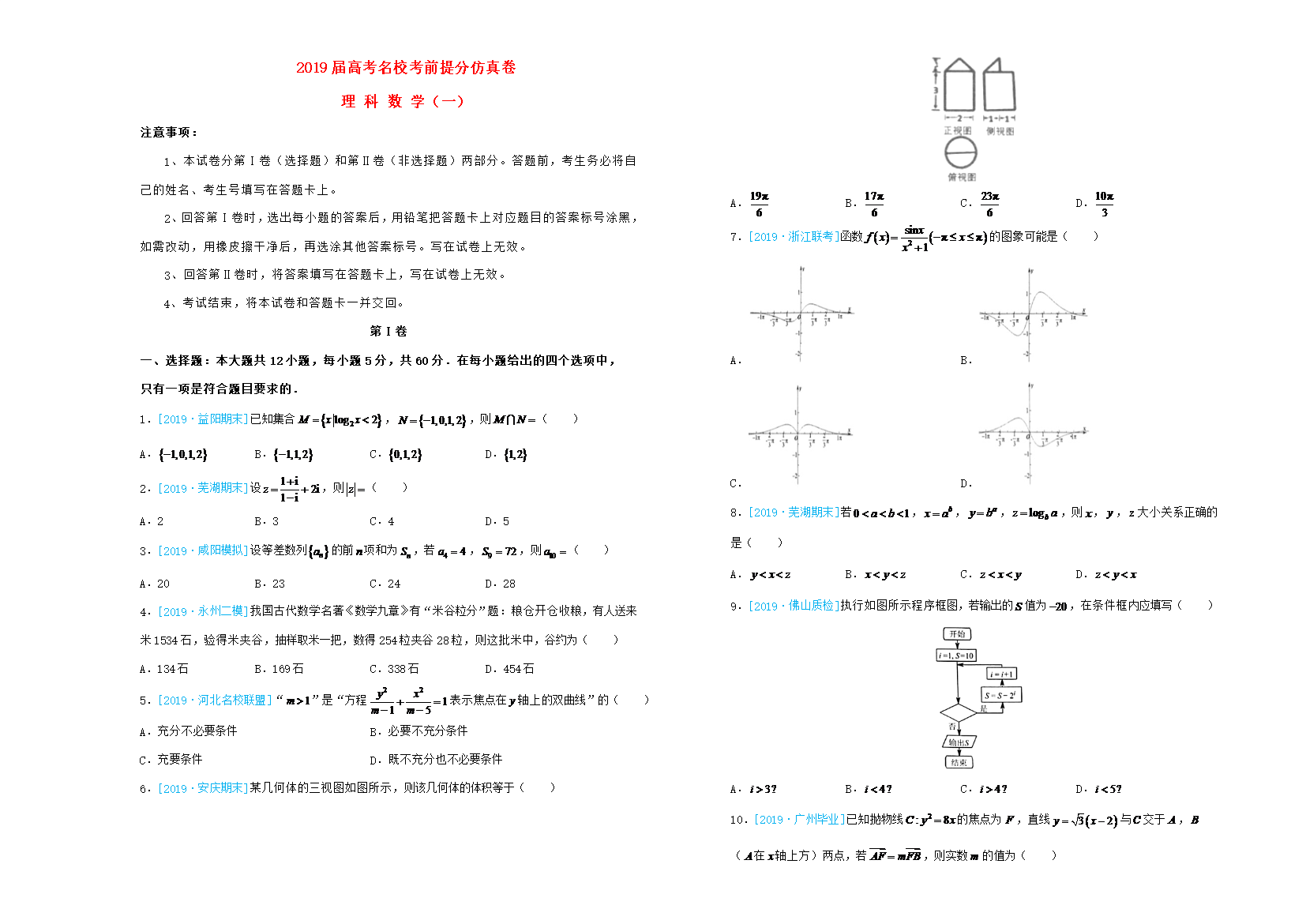
2019届高考名校考前提分仿真卷理科数学(一)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答题前,考生务必将自己的姓名、考生号填写在答题卡上。2、回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。写在试卷上无效。3、回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。4、考试结束,将本试卷和答题卡一并交回。第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
