
导数 课本中的新亮点 专题辅导 不分版本 试题.doc

春岚****23




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

导数 课本中的新亮点 专题辅导 不分版本 试题.doc
导数课本中的新亮点陈广田“导数”是新高中数学新增内容,它不仅是研究函数单调性、极值、最值、讨论函数图象变化趋势的重要工具,而且是学习高等数学的基础。因此,近几年高考中都把它作为重点内容进行考查。本文通过例题说明导数的一些应用。1.求切点坐标例1.曲线在P0点处的切线平行直线,则P0点的坐标为()A.(1,0)B.(2,8)C.(1,0)或(―1,―4)D.(2,8)或(―1,―4)解:因为,在P0点处的导数由,得即所以P0(1,0)和P0(―1,―4)故选C2.求函数的单调区间例2.函数的单调递增区间是(
高考新亮点 氯碱工业 专题辅导 不分版本.doc
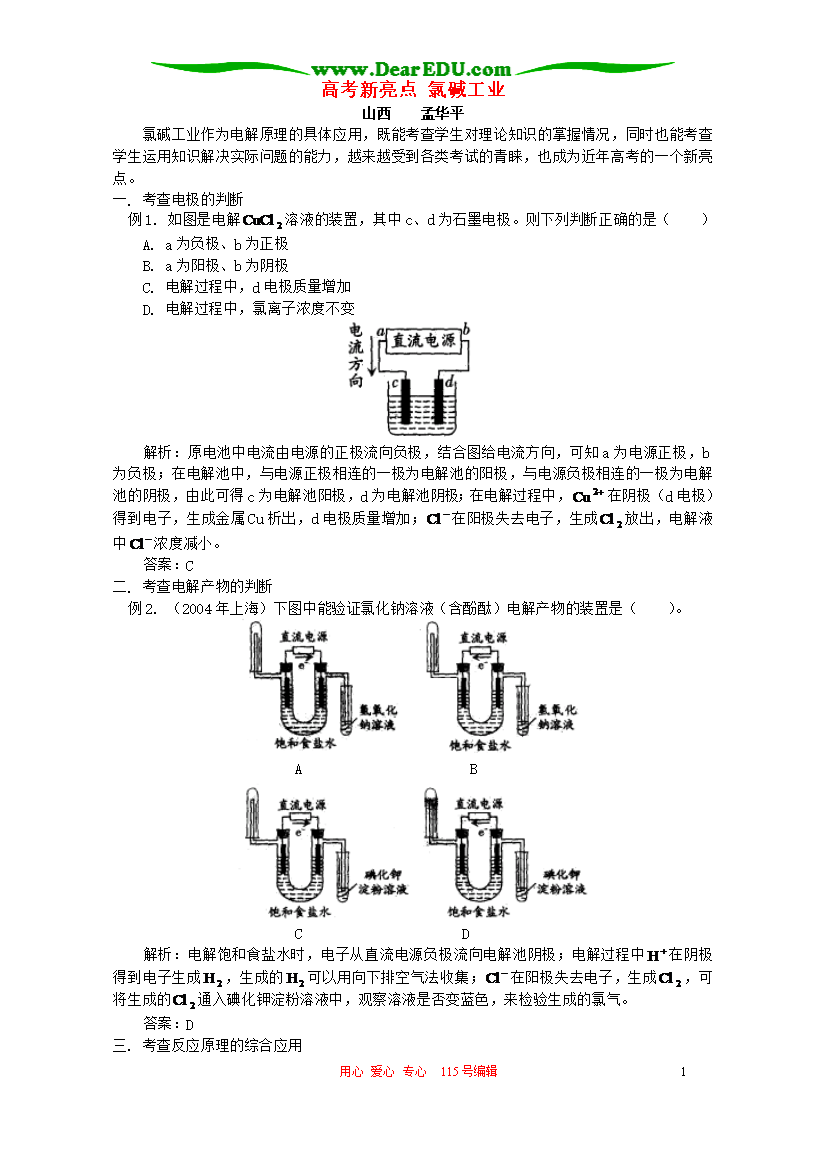
用心爱心专心115号编辑2高考新亮点氯碱工业山西孟华平氯碱工业作为电解原理的具体应用既能考查学生对理论知识的掌握情况同时也能考查学生运用知识解决实际问题的能力越来越受到各类考试的青睐也成为近年高考的一个新亮点。一.考查电极的判断例1.如图是电解溶液的装置其中c、d为石墨电极。则下列判断正确的是()A.a为负极、b为正极B.a为阳极、b为阴极C.电解过程中d电极质量增加D.电解过程中氯离子浓度不变解析:原电池中电流

高考新亮点 氯碱工业 专题辅导 不分版本.doc
用心爱心专心115号编辑高考新亮点氯碱工业山西孟华平氯碱工业作为电解原理的具体应用,既能考查学生对理论知识的掌握情况,同时也能考查学生运用知识解决实际问题的能力,越来越受到各类考试的青睐,也成为近年高考的一个新亮点。一.考查电极的判断例1.如图是电解溶液的装置,其中c、d为石墨电极。则下列判断正确的是()A.a为负极、b为正极B.a为阳极、b为阴极C.电解过程中,d电极质量增加D.电解过程中,氯离子浓度不变解析:原电池中电流由电源的正极流向负极,结合图给电流方向,可知a为电源正极,b为负极

回归课本 课本中习题变型题集 专题辅导 不分版本 试题.doc
回归课本课本中习题变型题集姚强一、选择题1.()A.B.C.D.2.=()A.B.C.D.3.已知是钝角,那么是()A.不小于直角的正角B.第二象限角C.第一象限与第二象限角D.第一象限角4.已知角α的正切线是单位长度的有向线段,则角α的终边()A.在x轴上B.在y轴上C.在直线y=x上D.在直线y=x上或y=-x上5.下列结论不正确的是()A.B.C.D.(α为第二象限角)6.下列结论不正确的是()A.B.C.D.7.下列结论正确的是()A.B.C.D.8.的倾斜角是()A.1B.C.D.9.函数()在

回归课本 课本中习题变型题集 专题辅导 不分版本.rar
用心爱心专心122号编辑4回归课本课本中习题变型题集姚强一、选择题1.()A.B.C.D.2.=()A.B.C.D.3.已知是钝角,那么是()A.不小于直角的正角B.第二象限角C.第一象限与第二象限角D.第一象限角4.已知角α的正切线是单位长度的有向线段,则角α的终边()A.在x轴上B.在y轴上C.在直线y=x上D.在直线y=x上或y=-x上5.下列结论不正确的是()A.B.C.D.(α为第二象限角)6.下列结论不正确的是()A.B.C.D.7.下列结论正确的是()A.B.C.D.8.的倾斜角是()A.1
