八年级数学暑假专题 等腰梯形常见辅助线的作法及梯形中位线定理和应用 鲁教版 知识精讲 试题.doc

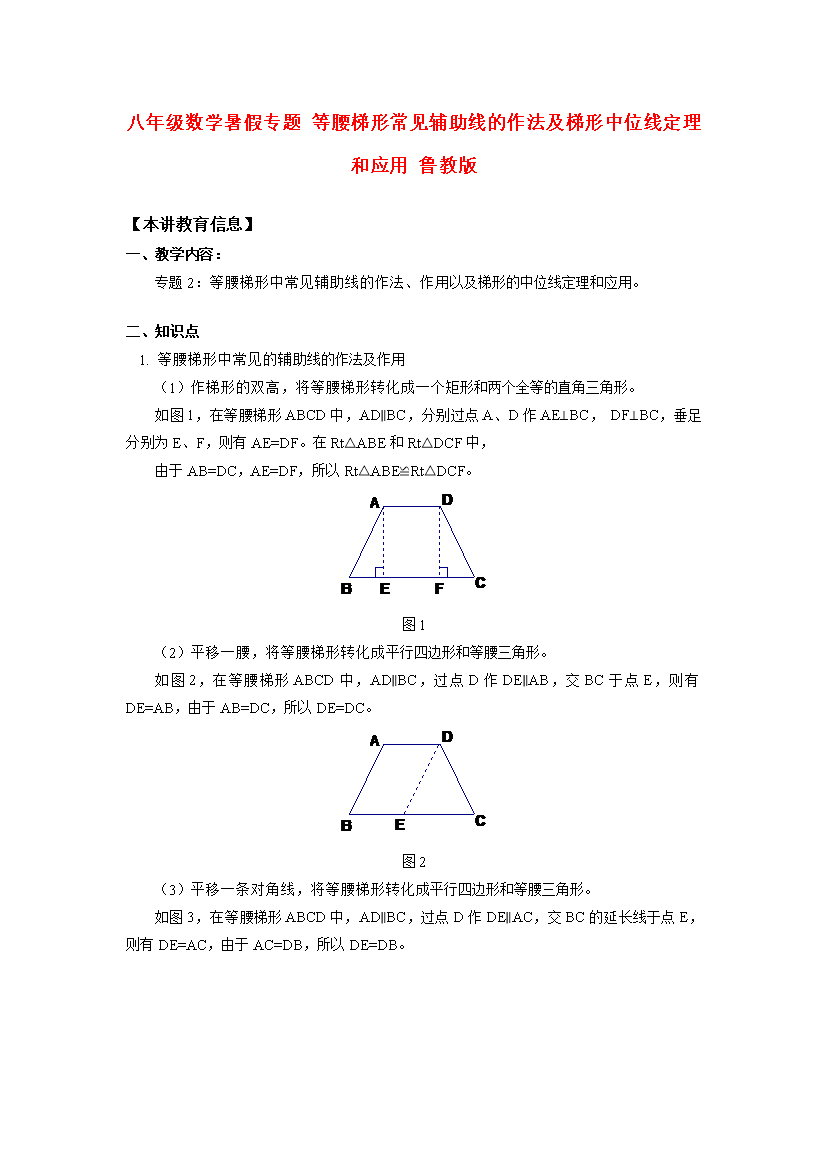
八年级数学暑假专题等腰梯形常见辅助线的作法及梯形中位线定理和应用鲁教版【本讲教育信息】一、教学内容：专题2：等腰梯形中常见辅助线的作法、作用以及梯形的中位线定理和应用。二、知识点1.等腰梯形中常见的辅助线的作法及作用（1）作梯形的双高，将等腰梯形转化成一个矩形和两个全等的直角三角形。如图1，在等腰梯形ABCD中，AD∥BC，分别过点A、D作AE⊥BC，DF⊥BC，垂足分别为E、F，则有AE=DF。在Rt△ABE和Rt△DCF中，由于AB=DC，AE=DF，所以Rt△ABE≌Rt△DCF。图1（2）平移一腰，将等腰梯形转化成平行四边形和等腰三角形。如图2，在等腰梯形ABCD中，AD∥BC，过点D作DE∥AB，交BC于点E，则有DE=AB，由于AB=DC，所以DE=DC。图2（3）平移一条对角线，将等腰梯形转化成平行四边形和等腰三角形。如图3，在等腰梯形ABCD中，AD∥BC，过点D作DE∥AC，交BC的延长线于点E，则有DE=AC，由于AC=DB，所以DE=DB。图32.梯形的中位线（1）梯形的中位线定义：如图4，连接梯形的两腰中点的线段，叫做梯形的中位线。图4（2）梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半。如图4，在梯形ABCD中，AD∥BC，点E、F分别是梯形两腰的中点，则EF∥AD∥BC，。（3）梯形中位线定理的作用：=1\*GB3①证明线段平行；=2\*GB3②证明一条线段等于另外两条线段和的一半。（4）梯形中位线定理的证明：教材上的证明方法：如图5，连接AF并延长，交BC的延长线于点G，将梯形的中位线转化成三角形的中位线，进一步完成证明。这条辅助线也是梯形中常见的辅助线。图5构建平行四边形完成证明：如图6，过点F作GH∥AB，交BC于点G，交AD的延长线于点H，证明四边形AEFH是平行四边形，进一步完成证明。图6梯形的中位线以及证明梯形中位线定理的辅助线，也是梯形中常见的辅助线。三、重点难点重点：等腰梯形常见的辅助线作法与作用以及梯形的中位线性质及其应用。难点：作恰当的辅助线解决梯形问题。四、考点分析梯形是除了平行四边形以外，另一种特殊的四边形。梯形的辅助线能很好的考查同学们转化图形的能力。因此，梯形（特别是等腰梯形）是中考出题的重点。【典型例题】例1.如图，梯形ABCD中，AD∥BC，AD=2cm，BC=7cm，AB=4cm。试确定DC的取值范围。分析：确定线段的取值范围，基本思路是将线段转化成三角形的三条边之间的关系，利用三角形的三边关系求线段的取值范围。解：如图，过点D作DE∥AB，交BC于点E，由于AD∥BC，所以四边形ABED是平行四边形。所以AD=BE=2cm，AB=DE=4cm。所以CE=BC－BE=5cm。在△DEC中，由于DE+EC>DC；EC－DE<DC，所以DC的取值范围是：1cm<DC<9cm。评析：通过平移梯形的腰，将梯形的两底和两腰转化成一个三角形的三边关系，利用三角形的三边关系求线段的取值范围。例2.如图，梯形ABCD中，AD∥BC，（BC>AD），∠B+∠C=90°，M、N分别是AD和BC的中点。求证：分析：过点M分别作两腰的平行线，则有∠MGH=∠B，∠MHG=∠C。由于∠B+∠C=90°，因此，在△MGH中，∠MGH+∠MHG=90°，△MGH是一个直角三角形。证明：过点M作MG∥AB，MH∥CD，分别交BC于点G、H。∵AD∥BC，∴四边形ABGM和四边形MHCD都是平行四边形。∴∠MGH=∠B，∠MHG=∠C。∵∠B+∠C=90°，∴∠MGH+∠MHG=90°，即△MGH是一个直角三角形。∵AM=BG，MD=CH，AM=DM，∴BG=CH，GH=BC－AD。∵BN=CN，∴GN=HN，即点N是线段GH的中点。∴在Rt△MGH中，。∴。评析：根据题目的需要，既可以将梯形的一腰平移到需要的位置，也可以根据需要同时平移两腰，完成图形的转化。例3.如图，在等腰梯形ABCD中，AD∥BC，AB=DC，AC=BC+AD。求∠DBC的度数。分析：平移一条对角线，将梯形的两底和对角线转化成三角形的三条边。解：如图，过点D作DE∥AC，交BC的延长线于点E，由于AD∥BC，所以四边形ACED是平行四边形。所以，AD=CE，AC=DE。即BE=BC+AD。由于AC=BD，AC=BC+AD，所以BD=BE=DE，即△BDE是一个等边三角形，所以∠DBC=60°。评析：在等腰梯形中，见到与对角线相关的条件，往往通过平移对角线完成图形的转化。例4.如图，梯形ABCD中，AB∥CD，AB=2，BC=3，CD=1，E是AD中点。求证：CE⊥BE。分析：作梯形的中位线，或延长CE交BA的延长线于点F，将梯形的两底和腰BC转化成一个三角形的边角关系。证明：方法一、如图，作梯形的中位