一种基于变分模态分解和人工蜂群优化的短期电力负荷预测方法.pdf

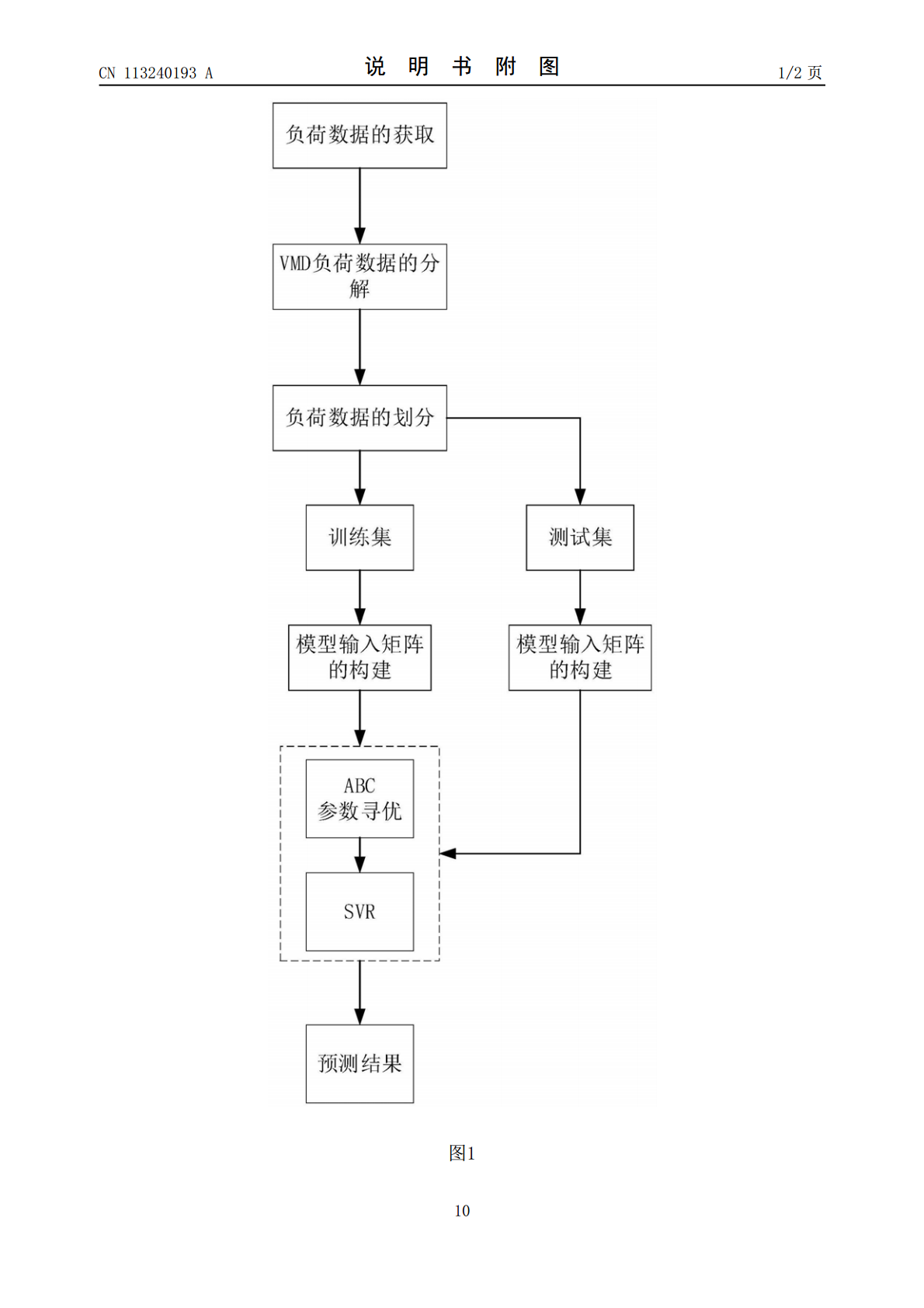
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号CN113240193A(43)申请公布日2021.08.10(21)申请号202110622868.5(22)申请日2021.06.03(71)申请人安徽理工大学地址232001安徽省淮南市山南新区泰丰大街168号(72)发明人胡天羽周孟然卞凯胡锋来文豪孙磊褚海波(51)Int.Cl.G06Q10/04(2012.01)G06Q10/06(2012.01)G06Q50/06(2012.01)G06K9/62(2006.01)G06N3/00(2006.01)权利要求书3页说明书5页附图2页(54)发明名称一种基于变分模态分解和人工蜂群优化的短期电力负荷预测方法(57)摘要本发明公开一种基于模态分解和群优化算法的短期电力负荷预测方法，涉及电力负荷预测领域和人工智能领域，包含以下步骤：(1)负荷数据的获取(2)负荷数据的分解。(3)负荷数据的划分。(4)模型输入矩阵的构建。(5)预测模型的构建。本发明采用VMD对负荷序列进行分解，通过ABC算法对SVR的c和g参数进行寻优，构建ABC‑SVR模型对分解后的若干分量进行预测，具有较好的预测性能并且对于数据量的要求较小，具有较好的实践应用价值。CN113240193ACN113240193A权利要求书1/3页1.一种基于模态分解和群优化算法的短期电力负荷预测方法，其特征在于，包括以下步骤：(1)负荷数据的获取：采集地区每小时负荷需求数据。(2)负荷数据的分解：采用模态分解方法对采集的数据进行分解。(3)负荷数据的划分：按一定比例将分解后各分量的数据按照一定比例顺序划分为训练集和预测集。(4)模型输入矩阵的构建：基于负荷序列数据进行输入矩阵的构建。(5)预测模型的构建：通过优化算法对预测模型的参数进行寻优，构建预测负荷预测模型。2.根据权利要求1所述一种基于模态分解和群优化算法的短期电力负荷预测方法，其特征在于，所述步骤(2)中，采用变分模态分解(VariationalModeDecomposition，VMD)将数据分解为若干高频分量和若干低频分量，分量(IMF)的总数K由分解分量的中心频率决定，具体步骤如下：(21)初始化{λ1}和n；式中uk为模态函数，ωk为中心频率，λ为拉格朗日惩罚算子，α为二次惩罚因子，n为迭代次数。(22)按照下式更新uk：(23)按照下式更新ωk：(24)按照下式更新λ：(25)当迭代精度ε＞0，满足下式时终止迭代，获得K个IMF分量。(26)为了获得最优的分量数K，本发明通过分量中心频率进行判断，具体步骤如下：(261)当分量数设为K时，且分解出的K个分量中没有中心频率相近的时，K＝K+1。(262)再次进行模态分解，若仍无中心频率相近的分量，重复(261)步骤；若有中心频率相近的分量，K＝K‑1,K即为最佳模态分解数，将原始序列分解为K个分量。3.根据权利要求1所述一种基于模态分解和群优化算法的短期电力负荷预测方法，其特征在于，所述步骤(3)中，采用顺序划分的方式，将每一个分量的数据都按一定比例划分为不重复的训练集和预测集。4.根据权利要求1所述一种基于模态分解和群优化算法的短期电力负荷预测方法，其2CN113240193A权利要求书2/3页特征在于，所述步骤(4)中，模型输入矩阵由对分解后的K各模态分量的训练集、测试集，分别构建输入矩阵，预测模型的输入为预测时刻前m个小时的实际负荷数值，构建具体步骤如下：(41)分解后的第p个(p＝1,2,3…K)模态分量的训练集输入构建过程如下:根据样本数据产生A(m×s),样本数为n，s＝n‑m(n>m)即式：式中，a1,a2,...an1为对应时刻的负荷数值。(42)其余分量的训练集、测试集输入矩阵如(41)。5.根据权利要求1所述一种基于模态分解和群优化算法的短期电力负荷预测方法，其特征在于，所述步骤(5)中，采用支持向量回归(SVR)对负荷进行预测，并采用人工蜂群算法(ABC)对SVR模型进行参数优化，具体步骤如下：(51)分解后的第p个(p＝1,2,3…K)模态分量预测模型构建过程如下：(511)选择径向基函数(RadialBasisFunction，RBF)作为SVR的核函数；(512)惩罚系数c和核函数参数g设定在[lb,ub](ub,lb分别代表搜索范围的上下限)范围内；(513)初始化生成含有N个解的初始种群，每个解xi(i＝1,2,…N)，用一个2维向量(xi1,Txi2)来表示，产生的初始解如下式所示:xi＝lb+(ub‑lb)·rand(0,1)(514)对食物源即最优解进行搜索，具体如下式所示：zij＝xij+rij(xij‑xkj)式中，j∈{1,2},k∈{1,2,...,N},j和k都是随机选取但k≠j；ri