第二章点、直线、平面的投影.ppt

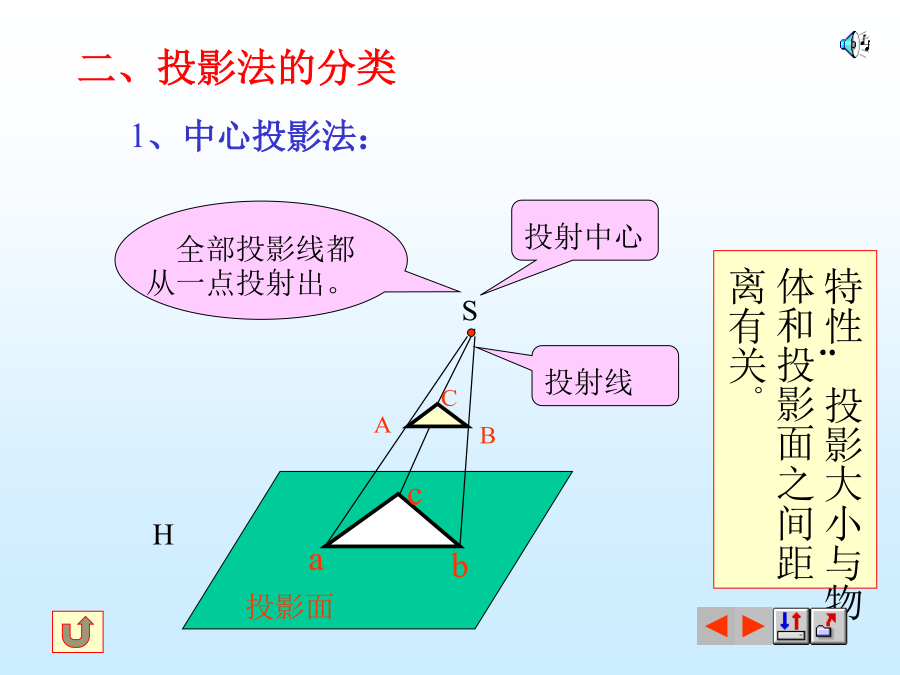
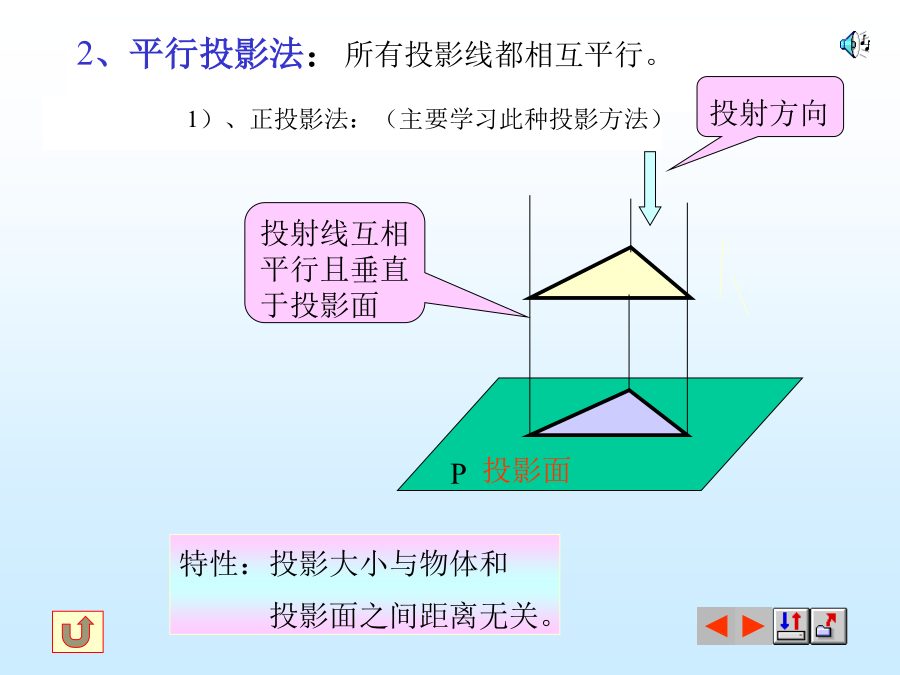
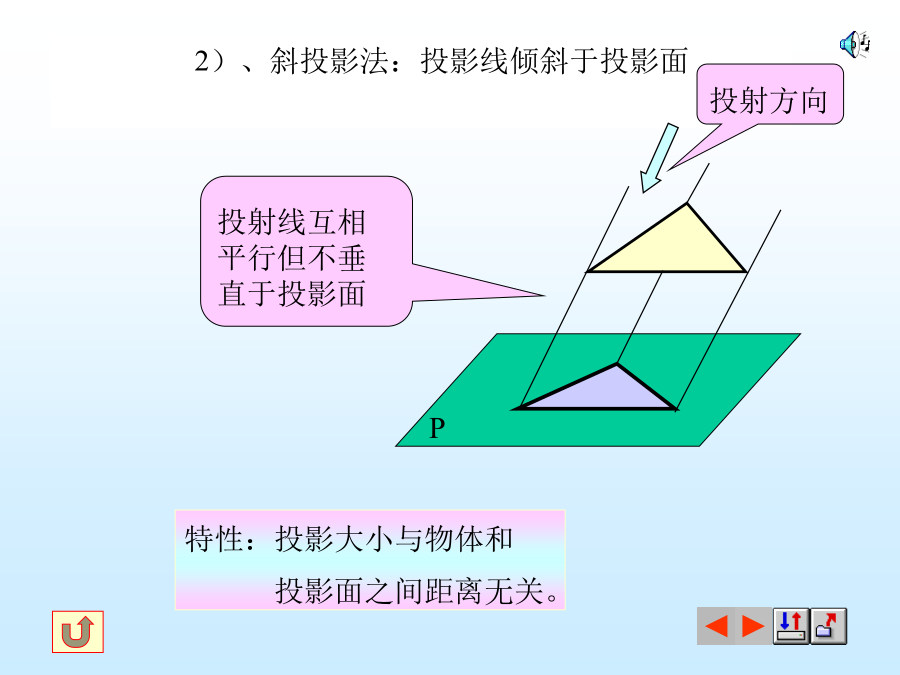
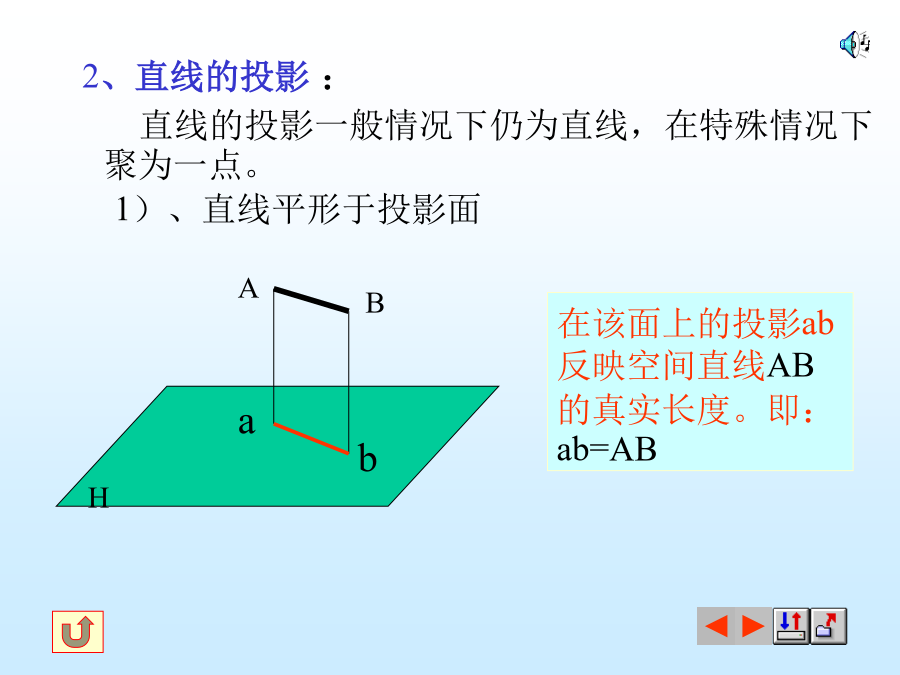
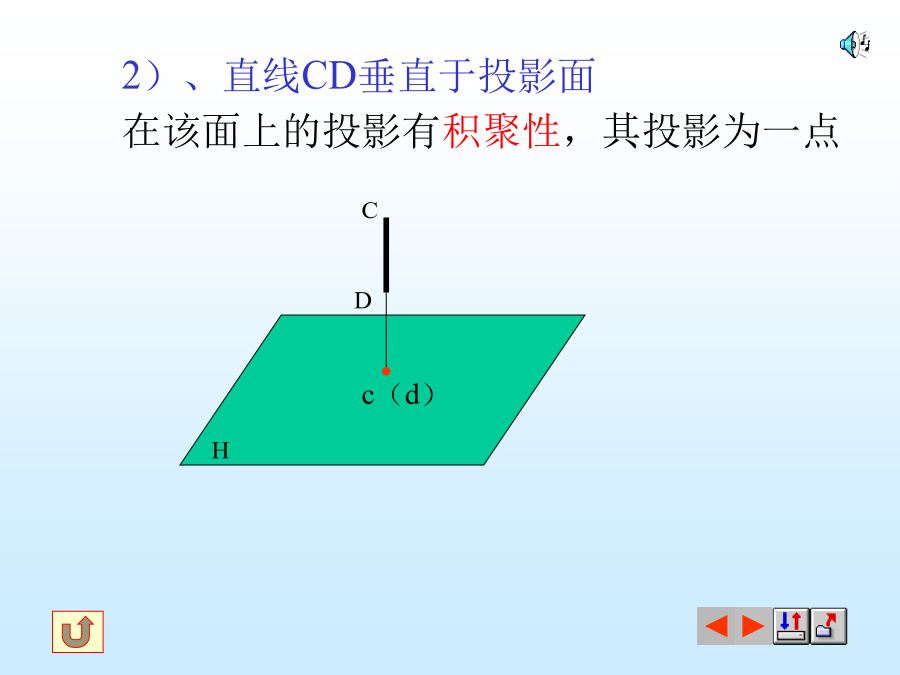
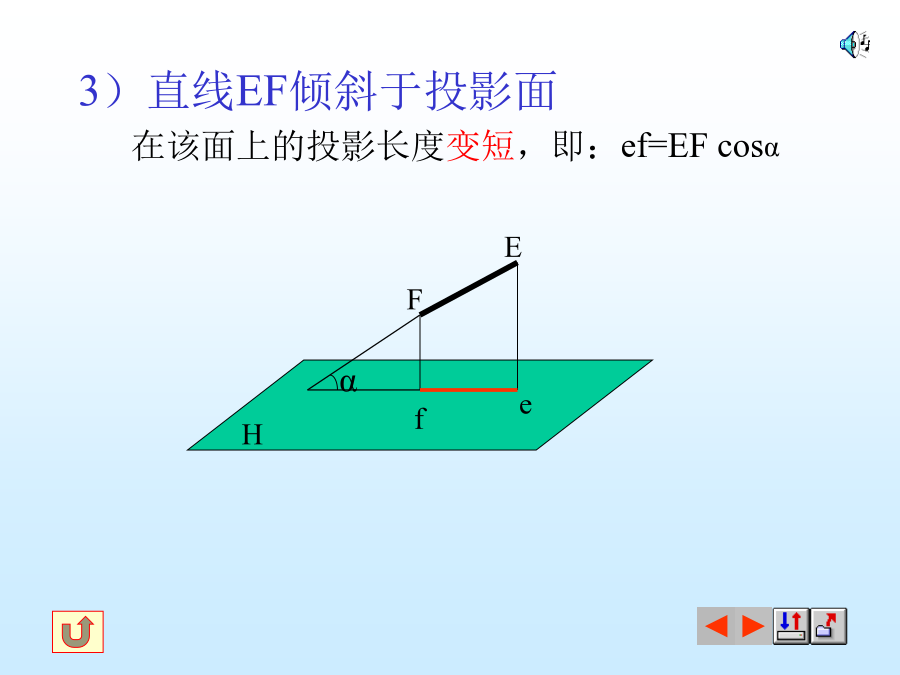
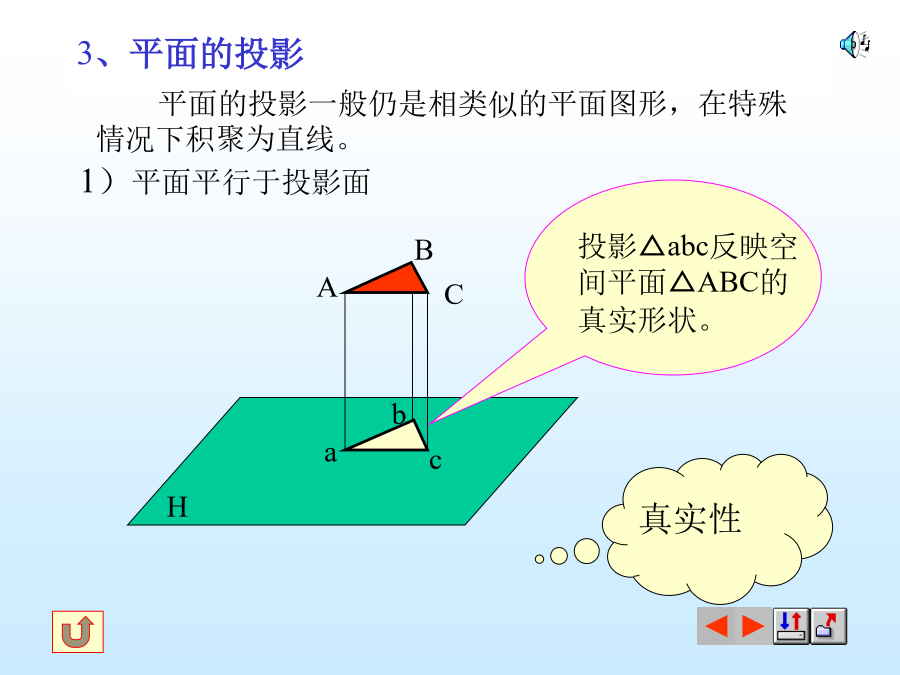
第一节投影法的基本知识一、投影的概念投影——空间物体在光线的照射下，在地上或墙上产生的影子，这种现象叫做投影。投影法——在投影面上作出物体投影的方法称为投影法。1、中心投影法：2、平行投影法：所有投影线都相互平行。2）、斜投影法：投影线倾斜于投影面三、正投影法的主要特性1、点的投影：2、直线的投影：2）、直线CD垂直于投影面在该面上的投影有积聚性，其投影为一点3）直线EF倾斜于投影面在该面上的投影长度变短，即：ef=EFcosα3、平面的投影2）、平面垂直于投影面3）平面倾斜于投影面四、投影的基本性质：★1、真实性★2、积聚性★3、类似性五、物体的三面投影图2、物体在三投影面体系中的投影俯§2--2点的投影V点的两面投影规律：二、点在三投影面体系中的投影点的三面投影规律：（1）、点的投影连线垂直于投影轴。即：a'a⊥ox，a'a"⊥oz（2）、点的投影到投影轴的距离，等于该点的坐标，也就是该点到相应投影面的距离。三、点的三面投影与直角坐标的关系：将投影面体系当作空间直角坐标系，把V、H、W当作坐标面，投影轴ox、oy、oz当作坐标轴，o作为原点。点A的空间位置可以用直角坐标（x，y，z）来表示。点A的x坐标值=oax=aay=a'az=Aa"反映点A到W面的距离。Y坐标值=oay=aax=a"az=Aa'反映点A到V面的距离。Z坐标值=oaz=a'ax=a"ay=Aa反映点A到H面的距离。例1、已知点的坐标值为：A（20，10，15）和B（0，15，20）求它们的三面投影图。例2、已知各点的两面投影，求作其第三投影，并判断点对投影面的相对位置。四、两点的相对位置和重影点：2、重影点例：已知点D的三面投影，点C在点D的正前方15mm，求作点C的三面投影，并判别其投影的可见性。Y§2--3直线的投影二、各种位置直线的投影特性2、投影面平行线2）、正平线：平行于V，对H、W倾斜3）、侧平线：平行于W面，对V、H面倾斜1、a′b′=AB=实长2、ab∥OX轴,a"b"∥OZ轴3、β=0°α、γ反映实际大小投影面平行线的投影特性3、投影面垂直线2）、正垂线：直线⊥V面，∥H、W面。3）、侧垂线：直线⊥W面，∥H、V面。1、V面投影积聚为一点。2、a"b"=ab=AB=实长3、ab⊥OX轴,a"b"⊥OZ轴β=90°α、γ=0°投影面垂直线的投影特性三、直线上的点2、定比性：例1、试在直线AB上取一点C，使AC:CB=1:2，求作C点。例2、已知直线CD及点M的两面投影，判断M是否在CD上。解2、四、两直线相对位置2、相交两直线O3、交叉两直线a例1、判断两直线的相对位置例2、过C点作水平线CD与AB相交。例3、已知：两直线AB、CD的投影及点M的水平投影m，试作一直线MN∥CD并与直线AB相交于N点。点与直线的投影特性，尤其是特殊位置直线的投影特性。点与直线及两直线的相对位置的判断方法及投影特性。点分割直线成定比——定比定理。§2--4平面的投影二、各种位置平面的投影1、投影面垂直面1、V面投影积聚成一条直线，且反映α、γ的真实大小。β=90°2、H、W投影均为原平面的类似形投影面垂直面的投影特性：平面在所垂直的投影面上的投影积聚为直线；其余两投影面仍为原形的类似形，但比实形小；平面具有积聚性的投影与投影轴的夹角，分别反映平面与相应投影面的倾角。2、投影面平行面V面投影反映实形，H、W投影积聚成一条直线，且分别平行与OX轴、OZ轴投影特性3、一般位置平面三、平面上的点和直线例1、已知△ABC平面内点K的V面投影k'，求作K的H面投影。例2、已知四边形ABCD的V面投影及AB、BC的H面投影，完成H面投影。2、平面上的投影面平行线例3、作△ABC平面内的正平线，它距V面为8mm。例4、在△ABC内取一点K，使点K距V面8mm，距H面12mm。四、特殊位置圆的投影2、与投影面垂直的圆§2--5直线与平面、平面与平面之间的相对位置例1、过点M作直线MN平行于平面△ABC。例2、过点M作直线MN平行于V面和△ABC。2、平面与平面平行例3、过点K作平面平行于△ABC例4、判别如图所示的两平面是否平行。二、直线与平面、平面与平面相交1、直线与平面相交交点是直线与平面的共有点。讨论：（1）求直线与平面的交点；（2）判别两者之间的相互遮挡关系，即判别可见性。例1、求直线AB与铅垂面△DEF的交点K，并判别可见性。例2、求直线AB与水平面的交点K，并判别可见性。2）、特殊位置直线（垂直线）与一般位置平面相交例3、求铅垂线DE与△ABC的交点K，并判别可见性。例4、求直线MN与平面△ABC的交点。2、平面与平面相交两平面相交，其交线为直线，交线是两平面的共有线，同时交线上的点是两平面的共有点。分析：∵△ABC与△DEF交线的正面投影为m'n'△DE