
中考数学复习 反比例函数复习素材 人教新课标版.doc

英哲****公主










亲,该文档总共13页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

中考数学复习 反比例函数复习素材 人教新课标版.doc
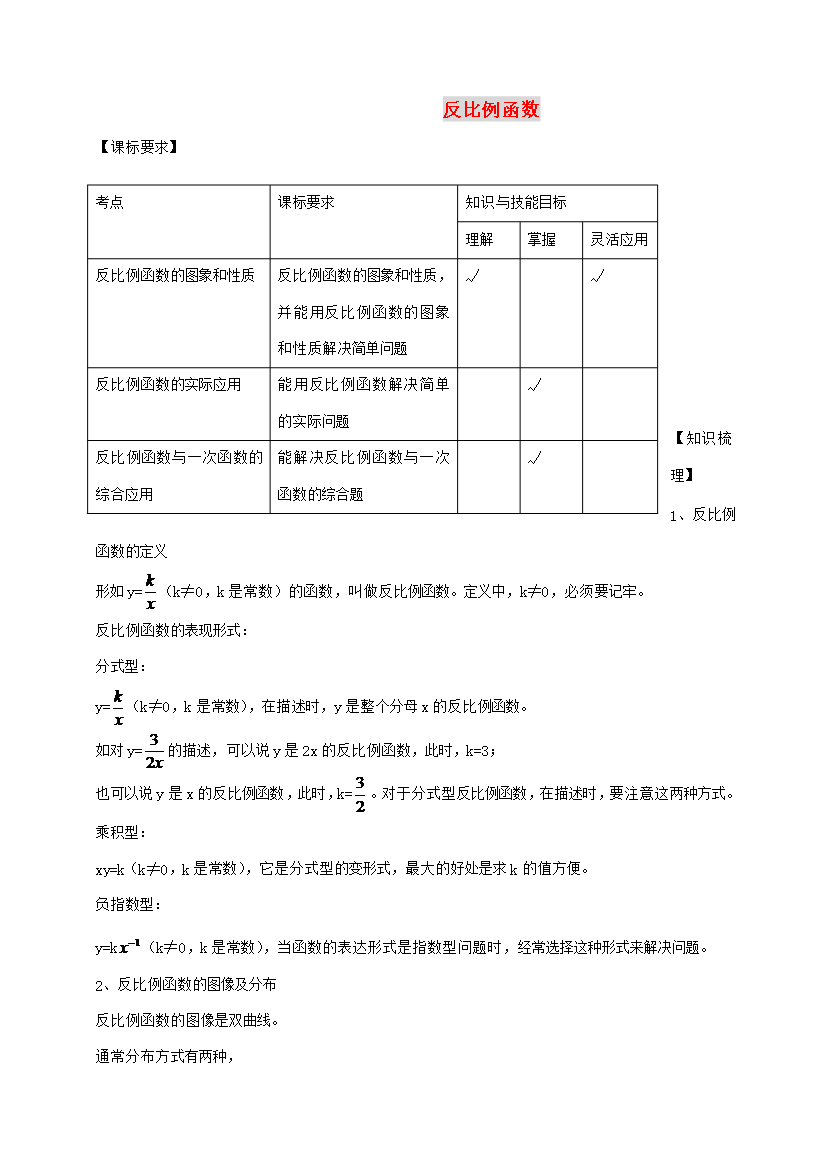
考点课标要求知识与技能目标理解掌握灵活应用反比例函数的图象和性质反比例函数的图象和性质,并能用反比例函数的图象和性质解决简单问题√√反比例函数的实际应用能用反比例函数解决简单的实际问题√反比例函数与一次函数的综合应用能解决反比例函数与一次函数的综合题√反比例函数【课标要求】【知识梳理】1、反比例函数的定义形如y=(k≠0,k是常数)的函数,叫做反比例函数。定义中,k≠0,必须要记牢。反比例函数的表现形式:分式型:y=(k≠0,k是常数),在描述时,y是整个分母x的反比例函数。如对y=的描述,可以说y是2x
中考数学复习 反比例函数复习素材 人教新课标版.doc
考点课标要求知识与技能目标理解掌握灵活应用反比例函数的图象和性质反比例函数的图象和性质并能用反比例函数的图象和性质解决简单问题√√反比例函数的实际应用能用反比例函数解决简单的实际问题√反比例函数与一次函数的综合应用能解决反比例函数与一次函数的综合题√反比例函数【课标要求】【知识梳理】1、反比例函数的定义形如y=(k≠0k是常数)的函数叫做反比例函数。定义中k≠0必须要记牢。反比例函数的表现形式:分式型:y=(k≠0k是常数)在描述时y是整个分母x的反比例函数。如对y=的描述可以说y是2x的反比例函数此时k

中考数学复习 反比例函数复习素材 人教新课标版.doc
考点课标要求知识与技能目标理解掌握灵活应用反比例函数的图象和性质反比例函数的图象和性质并能用反比例函数的图象和性质解决简单问题√√反比例函数的实际应用能用反比例函数解决简单的实际问题√反比例函数与一次函数的综合应用能解决反比例函数与一次函数的综合题√反比例函数【课标要求】【知识梳理】1、反比例函数的定义形如y=(k≠0k是常数)的函数叫做反比例函数。定义中k≠0必须要记牢。反比例函数的表现形式:分式型:y=(k≠0k是常数)在描述时y是整个分母x的反比例函数。如对y=的描述可以说y是2x的反比例函数此时k

中考数学 反比例函数总复习课件 人教新课标版 课件.ppt
第三章

教案-全国-2011_中考数学 反比例函数复习教案 人教新课标版.rar
用心爱心专心九年级数学第一轮复习学案设计反比例函数复习指导:反比例函数表达式的确定、反比例函数的图像和性质、反比例函数图像与一次函数图像的关系、利用反比例函数解决问题等都是中考的重要考点。一、目标导航1、会根据反比例函数的主要性质解决问题2、能在实际问题中建立反比例函数模型,进而解决问题复习重点1、反比例函数的性质2、综合反比例函数的知识解决综合问题二、自主探究考点链接:1.反比例函数:一般地,如果两个变量x、y之间的关系可以表示成y=或或(k为常数,k≠0)的形式,那么称y是x的反比例函数.2.反比例函
