数据拟合——线性回归.pdf

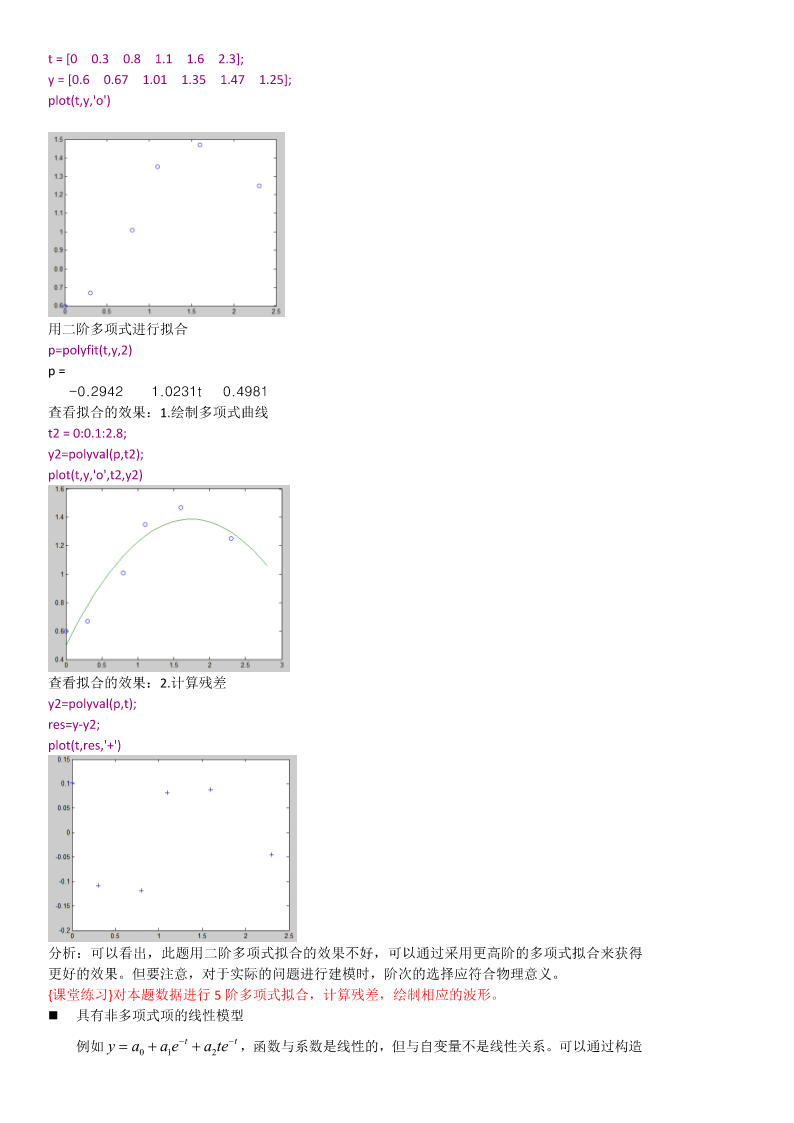
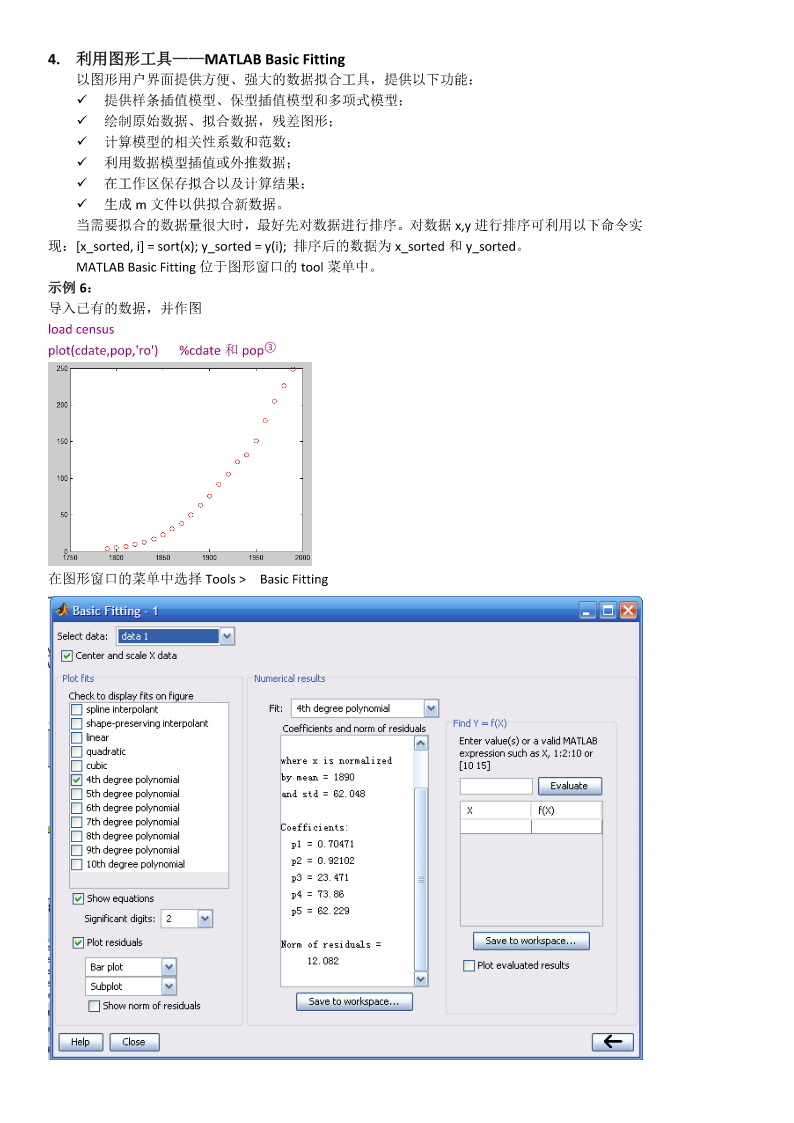
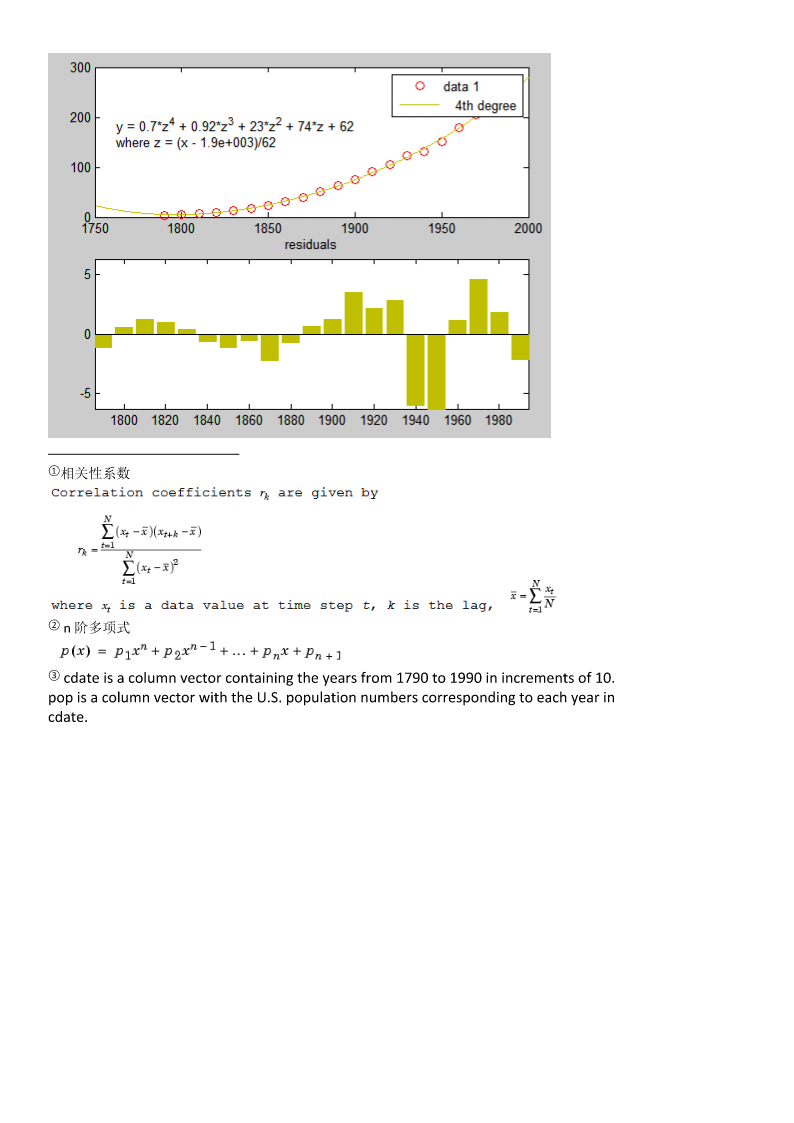
数据拟合——线性回归法【概述】MATLAB支持用户对数据用线性回归方法linearregression建立模型。模型是指自变量和因变量之间的关系。线性回归方法建立的模型的系数是线性的。最常用的线性回归方法是最小二乘拟合，可进行线性拟合和多项式拟合。1.线性相关性分析LinearCorrelationAnalysis在对两组测量数据建立关系模型前，最好对这些数据之间的关系作一个判断——相关性分析，看二者是否真的存在线性关系。这里，我们只介绍相关性系数①Correlationcoefficient的计算。简单的说，相关性系数是绝对值在0-1之间的数，其绝对值越接近1，表明数据之间存在线性关系的可能性越大。反之，数据越接近0，表明数据之间不太可能存在线性关系。MATLAB语法：R=corrcoef(x,y)计算数据x和y的相关系数矩阵R示例1：x=[12345678910];y=[149162536496481100];R=corrceof(x,y)R=1.00000.9746此数据表明两组数据具有很强的线性关系0.97461.0000示例2：x=[12345678910];y=[0.84150.90930.1411-0.7568-0.9589-0.27940.65700.98940.4121-0.5440];R=corrceof(x,y)R=1.0000-0.1705此数据表明两组数据不存在线性关系-0.17051.00002.评价数据拟合的优劣——残差计算残差被定义为实际测量数据与利用模型拟合（预测）的数据之差。合适的模型计算的残差应该接近独立的随机误差。如果计算得到的残差具有某种特殊的模式，那么模型就不合适。3.利用MATLAB函数进行数据拟合多项式模型MATLAB提供了2个用于多项式拟合的函数polyfit和polyval。MATLAB语法：p=polyfit(x,y,n)通过对数据x和y进行n阶多项式②拟合(基于最小二乘法)，计算n阶多项式系数pMATLAB语法：y=polyval(p,x)计算以p为系数的多项式，在x处的函数值y示例3：t=[00.30.81.11.62.3];y=[0.60.671.011.351.471.25];plot(t,y,'o')用二阶多项式进行拟合p=polyfit(t,y,2)p=-0.29421.0231t0.4981查看拟合的效果：1.绘制多项式曲线t2=0:0.1:2.8;y2=polyval(p,t2);plot(t,y,'o',t2,y2)查看拟合的效果：2.计算残差y2=polyval(p,t);res=y-y2;plot(t,res,'+')分析：可以看出，此题用二阶多项式拟合的效果不好，可以通过采用更高阶的多项式拟合来获得更好的效果。但要注意，对于实际的问题进行建模时，阶次的选择应符合物理意义。{课堂练习}对本题数据进行5阶多项式拟合，计算残差，绘制相应的波形。具有非多项式项的线性模型tt例如ya0a1ea2te，函数与系数是线性的，但与自变量不是线性关系。可以通过构造一组方程来解决系数的求解问题。示例4：%以列向量形式输入t和yt=[00.30.81.11.62.3]';y=[0.60.671.011.351.471.25]';%构造矩阵X=[ones(size(t))exp(-t)t.*exp(-t)];%计算系数a=X\ya=1.3983-0.88600.3085线性关系为y1.39830.886et0.3085tet查看拟合的效果：绘制多项式曲线T=(0:0.1:2.5)';Y=[ones(size(T))exp(-T)T.*exp(-T)]*a;plot(T,Y,'-',t,y,'o'),gridon多元回归当自变量不止一个时，如ya0a1x1a2x2。示例5：x1=[.2.5.6.81.01.1]';x2=[.1.3.4.91.11.4]';y=[.17.26.28.23.27.24]';X=[ones(size(x1))x1x2];a=X\ya=0.10180.4844-0.2847验证模型，计算最大残差的绝对值Y=X*a;MaxErr=max(abs(Y-y))MaxErr=0.0038此数据远小于y数据，说明此模式较好。4.利用图形工具——MATLABBasicFitting以图形用户界面提供方便、强大的数据拟合工具，提供以下功能：提供样条插值模型、保型插值模型和多项式模型；绘制原始数据、拟合数据，残差图形；计算模型的相关性系数和范数；利用数据模型插值或外推数据；在工作区保存拟合以及计算结果；生成m文件以供拟合新数据。当需要拟合的数据量很大时，最好先对数据进行排序。对数据x,y进行排序可利用以下命令实现：[