内容提供者
函数y＝Asin(ωx＋φ)的图象及应用.pptx
2024-06-14
10金币
1.7MB
24页
仙人****88
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共24页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
函数y＝Asin(ωx＋φ)的图象及应用.ppt
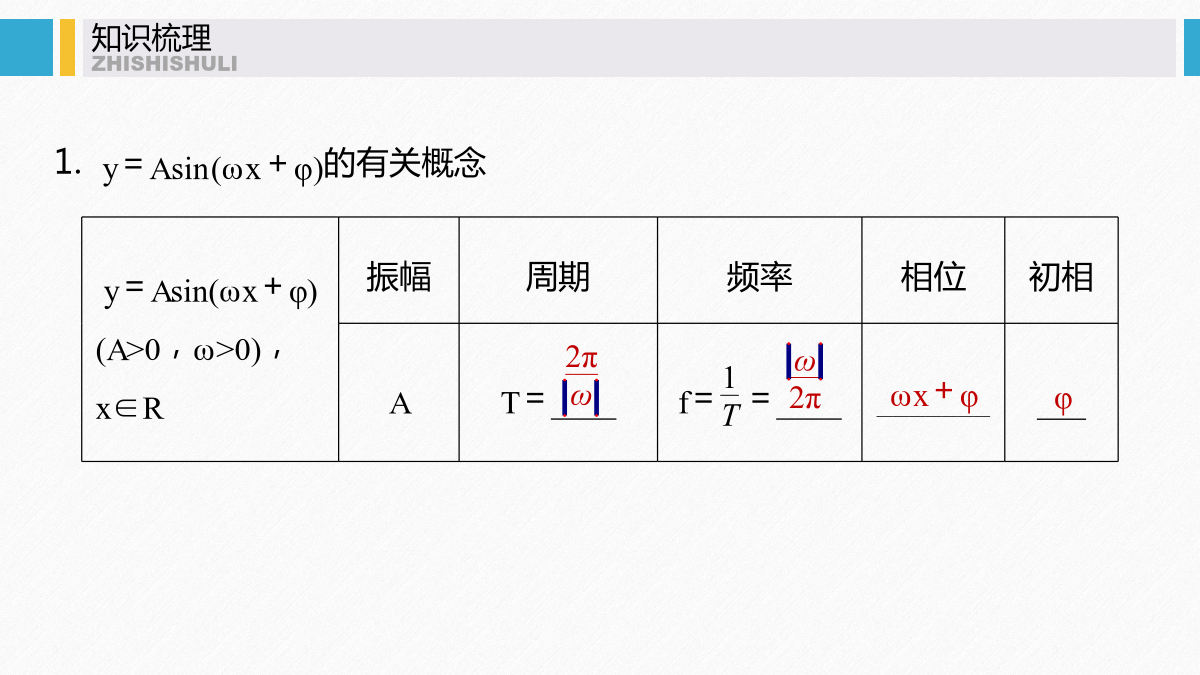
函数y＝Asin(ωx＋φ)的图象及应用基础自查1．用五点法画y＝Asin(ωx＋φ)一个周期内的简图时，要找五个特征点如下表所示2.函数y＝sinx的图象变换得到y＝Asin(ωx＋φ)的图象的步骤5．函数y＝Asin(ωx＋φ)(A，ω，φ为常数，A＞0，ω＞0)在闭区间[－π，0]上的图象如图所示，则ω＝________.考向一作函数y＝Asin(ωx＋φ)的图象列表，并描点画出图象：图象如图：考向二求函数y＝Asin(ωx＋φ)的解析式迁移发散考向三函数y＝Asin(ωx＋φ)的图象与性质的综合应
2024-06-15
10
697KB
函数y＝Asin(ωx＋φ)的图象及应用.pptx
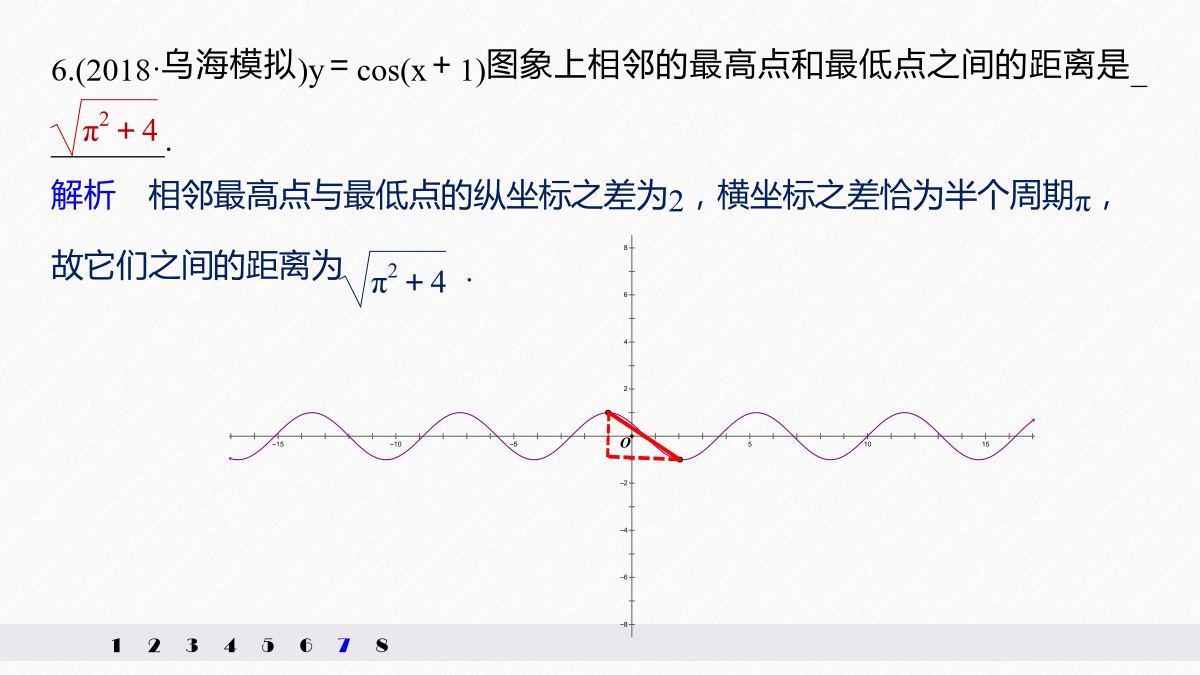
函数y＝Asin(ωx＋φ)的图象及应用11.y＝Asin(ωx＋φ)的有关概念3.函数y＝sinx的图象经变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种途径题组一思考辨析右2解因为函数f(x)的最小正周期是π，所以ω＝2.(2)作出f(x)在[0，π]上的图象(要列表).(2)作出f(x)在[0，π]上的图象(要列表).(1)y＝Asin(ωx＋φ)的图象可用“五点法”作简图得到，可通过变量代换z＝ωx＋φ计算五点坐标.(2)由函数y＝sinx的图象通过变换得到y＝Asin(ωx＋φ)的
2024-06-14
10
1.7MB
函数y＝Asin(ωx＋φ)的图象及应用.doc
高三一轮第四章第4讲三角函数y＝Asin(ωx＋φ)的图像和性质的学案一知识点梳理1.“五点法”作函数y＝Asin(ωx＋φ)(A>0，ω>0)的简图“五点法”作图的五点是在一个周期内的最高点、最低点及与x轴相交的三个点，作图时的一般步骤为：(1)定点：让学生列出表格.(2)作图：在坐标系中描出这五个关键点，用平滑的曲线顺次连接得到y＝Asin(ωx＋φ)在一个周期内的图象.(3)扩展：将所得图象，按周期向两侧扩展可得y＝Asin(ωx＋φ)在R上的图象.2.函数y＝Asin(ωx＋φ)中各量的物理意义当
2024-06-29
15
155KB
函数y=Asin(ωx+φ)的图象及应用.ppt
第4讲函数y＝Asin(ωx＋φ)的图象及应用基础自查1．用五点法画y＝Asin(ωx＋φ)一个周期内的简图时，要找五个特征点如下表所示2.函数y＝sinx的图象变换得到y＝Asin(ωx＋φ)的图象的步骤5．函数y＝Asin(ωx＋φ)(A，ω，φ为常数，A＞0，ω＞0)在闭区间[－π，0]上的图象如图所示，则ω＝________.考向一作函数y＝Asin(ωx＋φ)的图象列表，并描点画出图象：图象如图：考向二求函数y＝Asin(ωx＋φ)的解析式迁移发散考向三函数y＝Asin(ωx＋φ)的图象与性质的
2024-08-17
10
952KB
函数y＝Asin(ωx＋φ)的图象及应用.ppt
创新设计一轮复习第四章三角函数、解三角形最新考纲1.了解函数y＝Asin(ωx＋φ)的物理意义；能画出y＝Asin(ωx＋φ)的图象，了解参数A，ω，φ对函数图象变化的影响；2.会用三角函数解决一些简单实际问题，体会三角函数是描述周期变化现象的重要函数模型.忆一忆知识要点方法一y＝Asin(ωx＋φ)(A＞0,ω＞0),x∈[0,＋∞)诊断自测答案(1)×(2)×(3)√(4)√答案A答案D4.(2016·江苏卷)定义在区间[0，3π]上的函数y＝sin2x的图象与y＝cosx的图象的交点个数是_____
2024-06-29
15
7.9MB