
福建省中考数学复习 第五章 四边形 第二节 矩形、菱形、正方形课件-人教版初中九年级全册数学课件.ppt

An****99









亲,该文档总共16页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

福建省中考数学复习 第五章 四边形 第二节 矩形、菱形、正方形课件-人教版初中九年级全册数学课件.ppt
第二节矩形、菱形、正方形考点一矩形性质的相关计算例1(2016·漳州)一个矩形的面积为a2+2a若一边长为a则另一边长为.【分析】根据矩形的面积公式求解边长.【自主解答】∵(a2+2a)÷a=a+2∴另一边长为a+2.如图矩形ABCD中∠AOB=60°AB=2则AC的长为()A.2B.4C.2D.4考点二菱形性质的相关计算例2已知:如图菱形ABCD中对角线AC与BD相交于点OOE∥CD交BC于点EAD=6cm则OE的长为()A.6

福建省中考数学复习 第五章 四边形 第二节 矩形、菱形、正方形课件-人教级全册数学课件.ppt
第二节矩形、菱形、正方形考点一矩形性质的相关计算例1(2016·漳州)一个矩形的面积为a2+2a若一边长为a则另一边长为.【分析】根据矩形的面积公式求解边长.【自主解答】∵(a2+2a)÷a=a+2∴另一边长为a+2.如图矩形ABCD中∠AOB=60°AB=2则AC的长为()A.2B.4C.2D.4考点二菱形性质的相关计算例2已知:如图菱形ABCD中对角线AC与BD相交于点OOE∥CD交BC于点EAD=6cm则OE的长为()A.6

(东营专版)中考数学复习 第五章 四边形 第二节 矩形、菱形、正方形课件-人教版初中九年级全册数学课件.ppt
第二节矩形、菱形、正方形考点一矩形的性质与判定(5年1考)例1(2016·东营中考)如图在Rt△ABC中∠B=90°AB=4BC>AB点D在BC上以AC为对角线的平行四边形ADCE中DE的最小值是.【分析】首先利用平行四边形的性质得出AE∥CD从而当DE⊥BC时DE能够取得最小值再通过矩形的判定得出DE的最小值即可.【自主解答】∵四边形ADCE是平行四边形∴BC∥AE∴当DE⊥BC时DE最短.∵∠B=90°∴AB⊥BC∴DE∥AB∴四边形ABDE是平行四边形.∵∠B=90°∴四边形A

中考数学复习课件矩形菱形正方形.pptx
会计学知识点二菱形(línɡxínɡ)的定义、性质和判定知识点三正方形的定义(dìngyì)、性质和判定

河南省中考数学总复习 第五章 四边形 第二节 矩形、菱形、正方形课件-人教版初中九年级全册数学课件.ppt
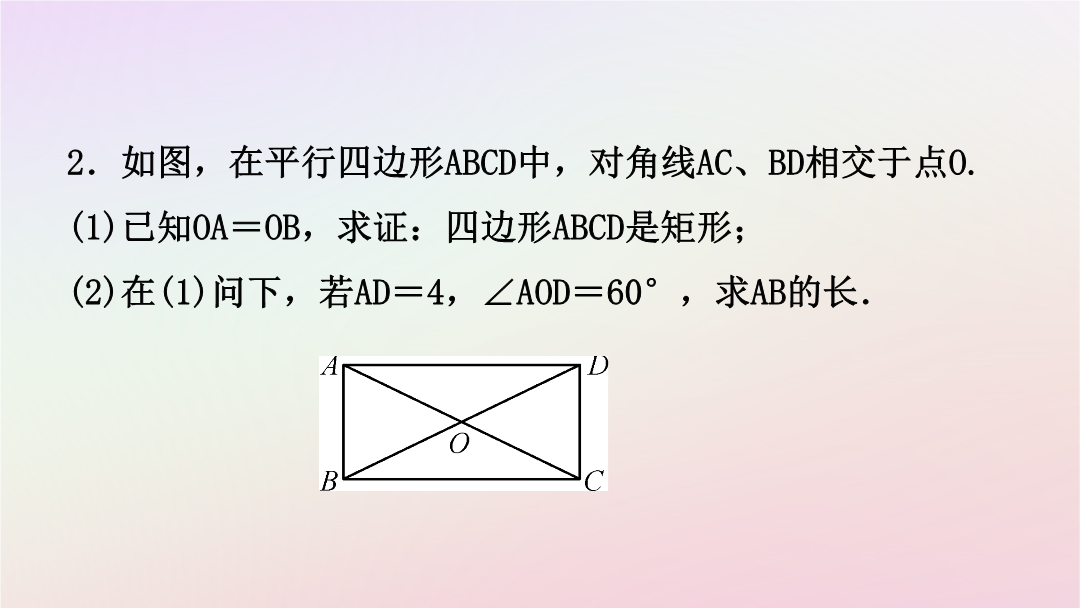
第二节矩形、菱形、正方形考点一矩形判定及性质的相关计算例1一个矩形的面积为a2+2a若一边长为a则另一边长为.【分析】根据矩形的面积公式求解边长.【自主解答】∵(a2+2a)÷a=a+2∴另一边长为a+2.如图在平行四边形ABCD中对角线AC、BD相交于点O.(1)已知OA=OB求证:四边形ABCD是矩形;(2)在(1)问下若AD=4∠AOD=60°求AB的长.(1)证明:∵在▱ABCD中OA=OC=ACOB=OD=BD.又∵OA=OB∴AC=BD∴四边形ABCD是矩形;(2)解:∵
