
绪论.pdf

努力****向丝









亲,该文档总共22页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

绪论必修一绪论.ppt
绪论判天地之美,析万物之理物理学是一门自然学科专家们想要确知,星星怎样出世,星星怎样去世······物理学是一门实验科学,也是一门崇尚理性、重视逻辑推理的科学。物理学与其他科学技术B-2隐形战略轰炸机物理学的每一次发展都促进了科学技术的进步,高新科技的发展离不开现代物理学。物理学与社会进步18世纪到19世纪,物理学家建立了热力学理论和分子物理,发现了能量转换和能量守恒定律后,开始探索用内能转化为机械能的方法来代替人力和畜力。这一伟大的发现,是以瓦特发明蒸汽机为代表的。蒸汽机的发明,直接推动了第一次工业革命

绪论分析化学绪论.ppt
分析化学课程任课教师注:分析化学教材与配套辅导教材分析化学(化学分析部分)理论课时安排第一章绪论§1分析化学的任务和作用中国《分析化学》2012年11期部分文章分散固相萃取净化气相色谱串联质谱法测定茶叶、西葫芦和芒果中噻螨酮和噻嗪酮残留量固相萃取-气相色谱质谱法检测水体中典型有机磷酸酯阻燃剂斑马鱼卵中多溴联苯醚及其衍生物的同步分析离子色谱柱切换法测定氟化盐高纯试剂中的阴离子杂质时间分辨荧光免疫法检测日本鳗鲡的产酸克雷伯氏菌罗丹明内酰胺和铜离子荧光法检测人工湿地中的磷酸根离子硫代乙酰胺键合硅胶在线选择性固相

绪论.docx
绪论绪论教学目标知识目标了解生物与生物科学的研究对象;了解生物的基本特征;了解生物科学的发展及高中生物学学习的主要内容;了解生物科学的研究方法;了解生物科学学习的意义和目标。能力目标在对生物特征的分析和讨论过程中,培养学生的思维能力和语言表达能力;在对生物科学研究方法的探究过程中,培养学生基本的科学探究意识和能力;在对生物科学发展的讨论中,培养学生收集、处理和表达信息的能力。情感目标在生物科学发展过程的讨论中,激发学习生物科学的兴趣;在对生物科学研究基本方法的探究过程中,培养学生科学探究的兴趣;在问题的讨

绪论.pdf
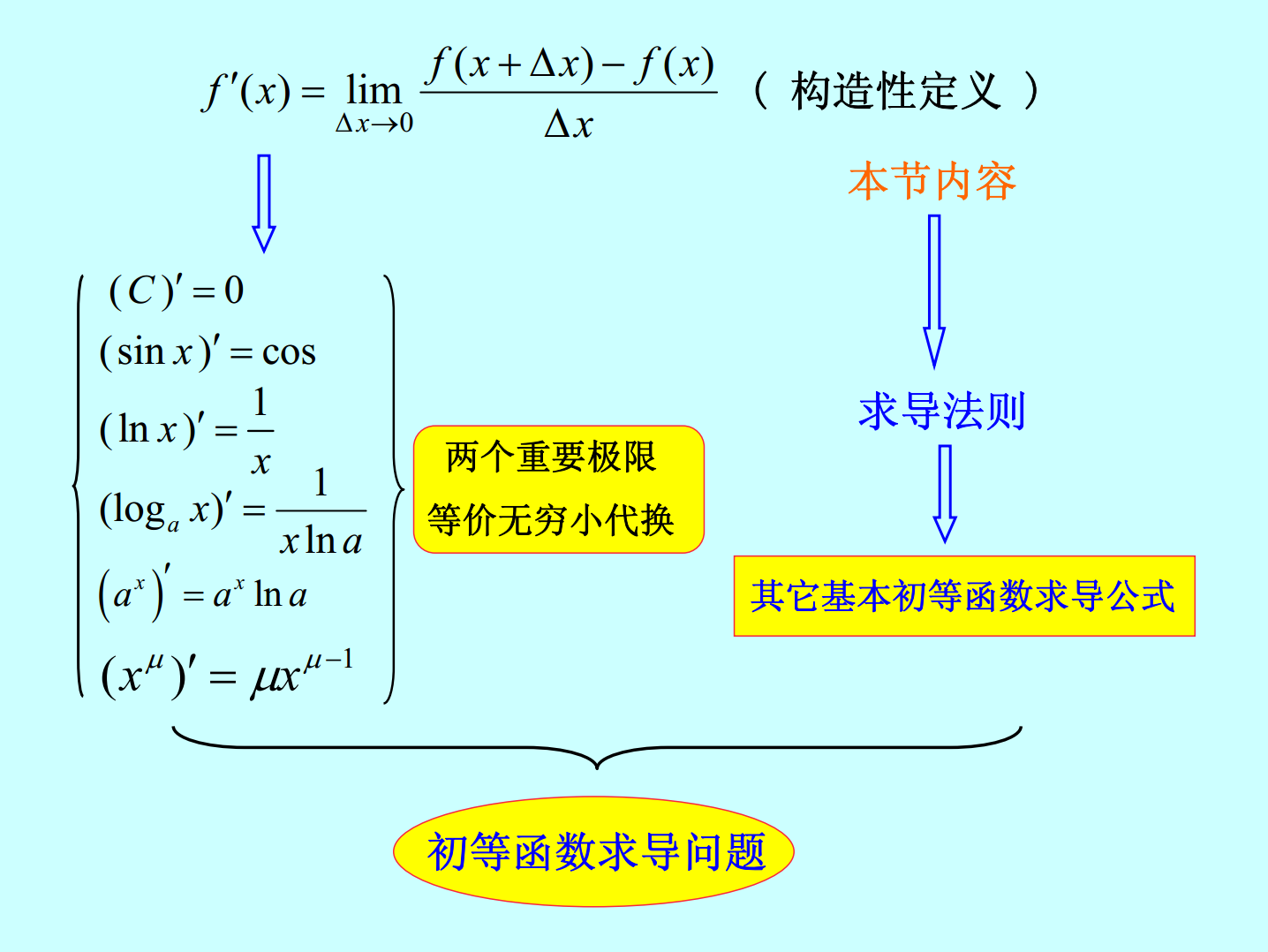
第二节求导法则z四则运算求导法则z反函数的求导法则z复合函数求导法则z一些特殊的求导法则+Δ−xfxxf)()(′xf=lim)((构造性定义)x→Δ0Δx本节内容()C′=0(sinx)′=cos1(lnx)′=求导法

绪论.doc
用心爱心专心绪论学习目标1、识记生物的基本特征2、知道生物科学的研究内容和发展过程及当代生物科学的新进展。难点突破应用生物的基本特征来解释常见的生物学现象自学导引一、生物的基本特征1.都有共同的物质基础和结构基础(1)物质基础:是生命活动的主要承担者,是遗传信息的携带者。(2)结构基础:除病毒以外,是生物体结构和功能的基本单位。2.都有新陈代谢作用(1)实质:生物体内全部有序的的总称。(2)意义:生物体进行的基础。3.都有应激性(1)概念:在的基础上,生物体对外界刺激产生一定的。(2)意义:
