
(通用版)高考数学大二轮复习 专题三 第2讲 数列求和与数列综合问题课件 理-人教版高三全册数学课件.pptx

一条****丹淑


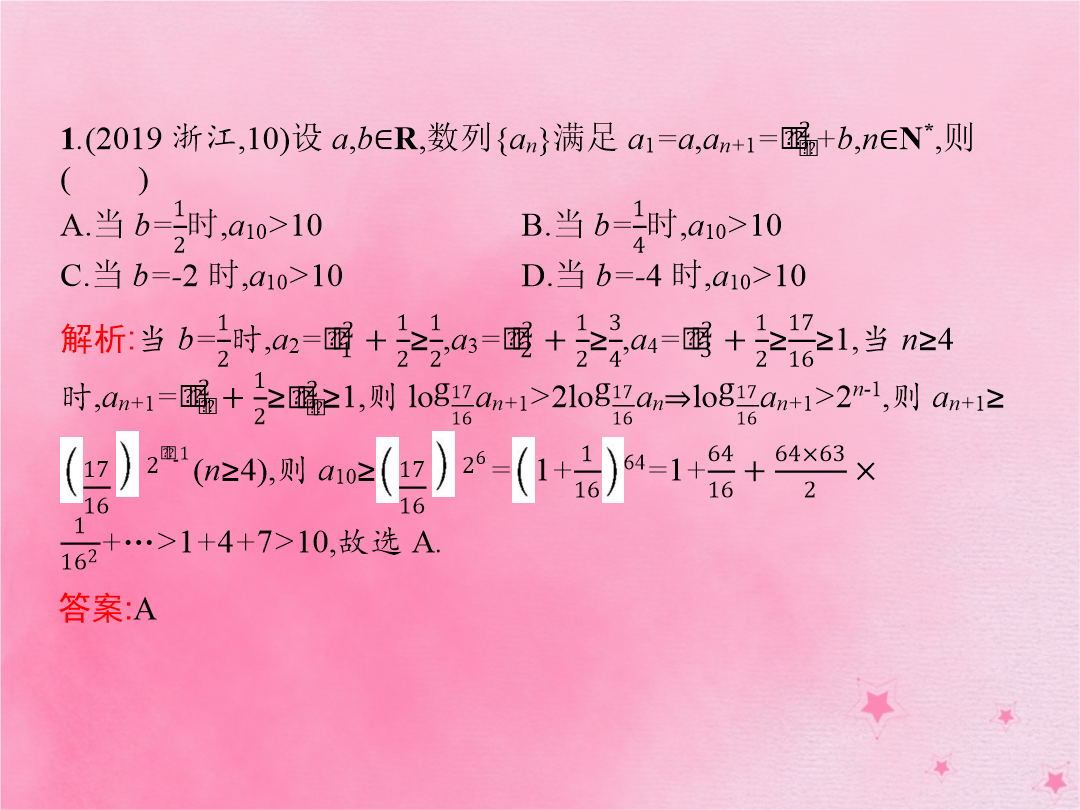







亲,该文档总共54页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

(通用版)高考数学大二轮复习 专题三 第2讲 数列求和与数列综合问题课件 理-人教版高三全册数学课件.pptx
第2讲数列求和与数列综合问题近五年高考试题统计与命题预测答案:A2.(2019全国Ⅱ理19)已知数列{an}和{bn}满足a1=1b1=04an+1=3an-bn+44bn+1=3bn-an-4.(1)证明:{an+bn}是等比数列{an-bn}是等差数列;(2)求{an}和{bn}的通项公式.3.(2019北京理20)已知数列{an}从中选取第i1项、第i2项、…、第im项(i1<i2<…<im)若

(通用版)高考数学大二轮复习 专题三 第2讲 数列求和与数列综合问题课件 文-人教版高三全册数学课件.pptx
第2讲数列求和与数列综合问题近五年高考试题统计与命题预测1.(2019全国Ⅰ文18)记Sn为等差数列{an}的前n项和.已知S9=-a5.(1)若a3=4求{an}的通项公式;(2)若a1>0求使得Sn≥an的n的取值范围.解:(1)设{an}的公差为d.由S9=-a5得a1+4d=0.由a3=4得a1+2d=4.于是a1=8d=-2.因此{an}的通项公式为an=10-2n.由a1>0知d<0故Sn≥an等价于n2-11n+10≤0解得1≤n≤10.所以n的取值范围是{n|1≤n≤10n∈N}.2.

高考数学二轮复习 第2部分 专题2 数列 第2讲 数列求和与综合问题课件 理-人教版高三全册数学课件.ppt
第二部分讲练篇自研Thankyouforwatching!
高考数学大二轮复习 第二部分 专题2 数列 第2讲 数列求和与数列的综合问题课件 文-人教版高三全册数学课件.ppt
第2讲数列求和与数列的综合问题利用递推关系或Sn、an的关系求an数列求和数列的应用与综合问题

高考数学二轮复习 专题二 数列 第2讲 数列求和及综合应用课件-人教版高三全册数学课件.ppt
第2讲数列求和及综合应用高考定位1.高考对数列求和的考查主要以解答题的形式出现通过分组转化、错位相减、裂项相消等方法求数列的和难度中档偏下;2.在考查数列运算的同时将数列与不等式、函数交汇渗透.解(1)因为a1+3a2+…+(2n-1)an=2n①故当n≥2时a1+3a2+…+(2n-3)an-1=2(n-1)②又S2n+1=bnbn+1bn+1≠0所以bn=2n+1.考点整合2.数列求和3.数列与函数、不等式的交汇解(1)因为an=5Sn+1n∈N*所以an+1=5Sn+1+1探究提高1
