高中数学221《直接证明与间接证明-综合法和分析法》课件新人教版选修2-2.ppt

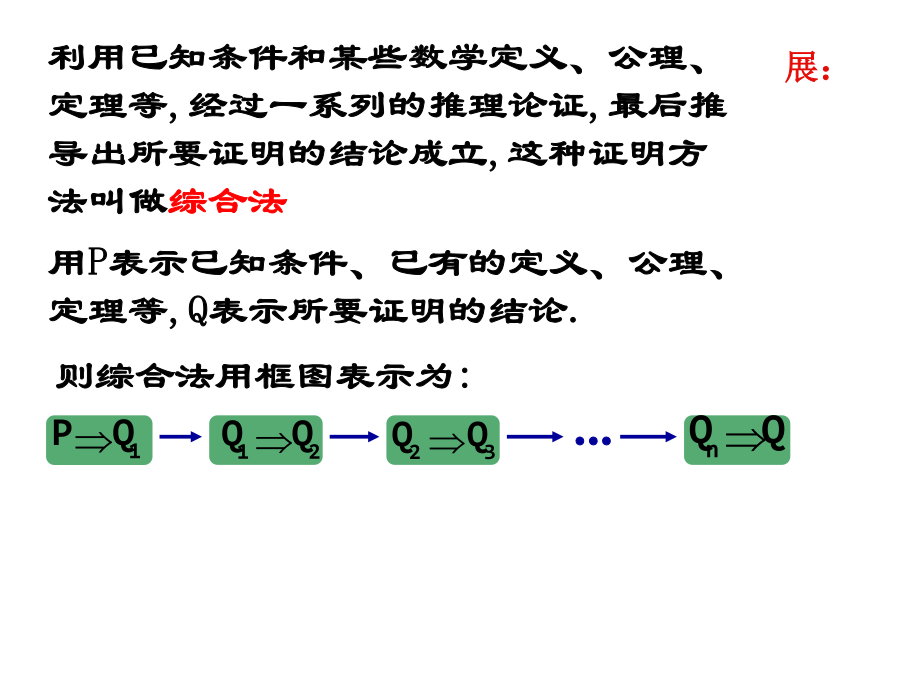
2.2.1《直接证明与间接证明-综合法和分析法》教学目标2.2直接证明与间接证明演绎推理是证明数学结论、建立数学体系的重要思维过程.例:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法例：在△ＡＢＣ中，三个内角Ａ、Ｂ、Ｃ对应的边分别为a、b、c，且Ａ、Ｂ、Ｃ成等差数列，a、b、c成等比数列，求证△ＡＢＣ为等边三角形．例：设抛物线y2=2px(p>0)的焦点为Ｆ，经过点Ｆ的直线交抛物线于Ａ、Ｂ两点，点Ｃ在抛物线的准线上，且ＢＣ∥x轴（如图），证明直线ＡＣ经过原点Ｏ作业：Ｐ１０２Ａ组２，Ｂ组２2.2直接证明与间接证明一般地，利用已知条件和某些已经学过的定义、定理、公理等，经过一系列的推理、论证，最后推导出所要证明的结论成立，这种证明方法叫做综合法。回顾基本不等式：(a>0,b>0)的证明.一般地，从要证明的结论出发，逐步寻求推证过程中，使每一步结论成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件（已知条件、定理、定义、公理等）为止，这种证明的方法叫做分析法．例:设a,b,c为一个三角形的三边,且s2=2ab,试证s<2a例:如图,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证AF⊥SC证:例:已知数列{an}的通项an>0,(n∈N*),它的前n项的和记为sn,数列{s2n}是首项为3,公差为1的等差数列.(1)求an与sn的解析式;(2)试比较sn与3nan(n∈N*),的大小.作业：Ｐ１０２Ａ组4，Ｂ组3思考题:甲、乙、丙三箱共有小球384个,先由甲箱取出若干放进乙、丙两箱内,所放个数分别为乙、丙箱内原有个数,继而由乙箱取出若干个球放进甲、丙两箱内,最后由丙箱取出若干个球放进甲、乙两箱内,方法同前.结果三箱内的小球数恰好相等.求甲、乙、丙三箱原有小球数再见