
黑龙江省牡丹江四中牛龙梅的上课教案.doc

鸿朗****ka






在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

黑龙江省牡丹江四中牛龙梅的上课教案.doc
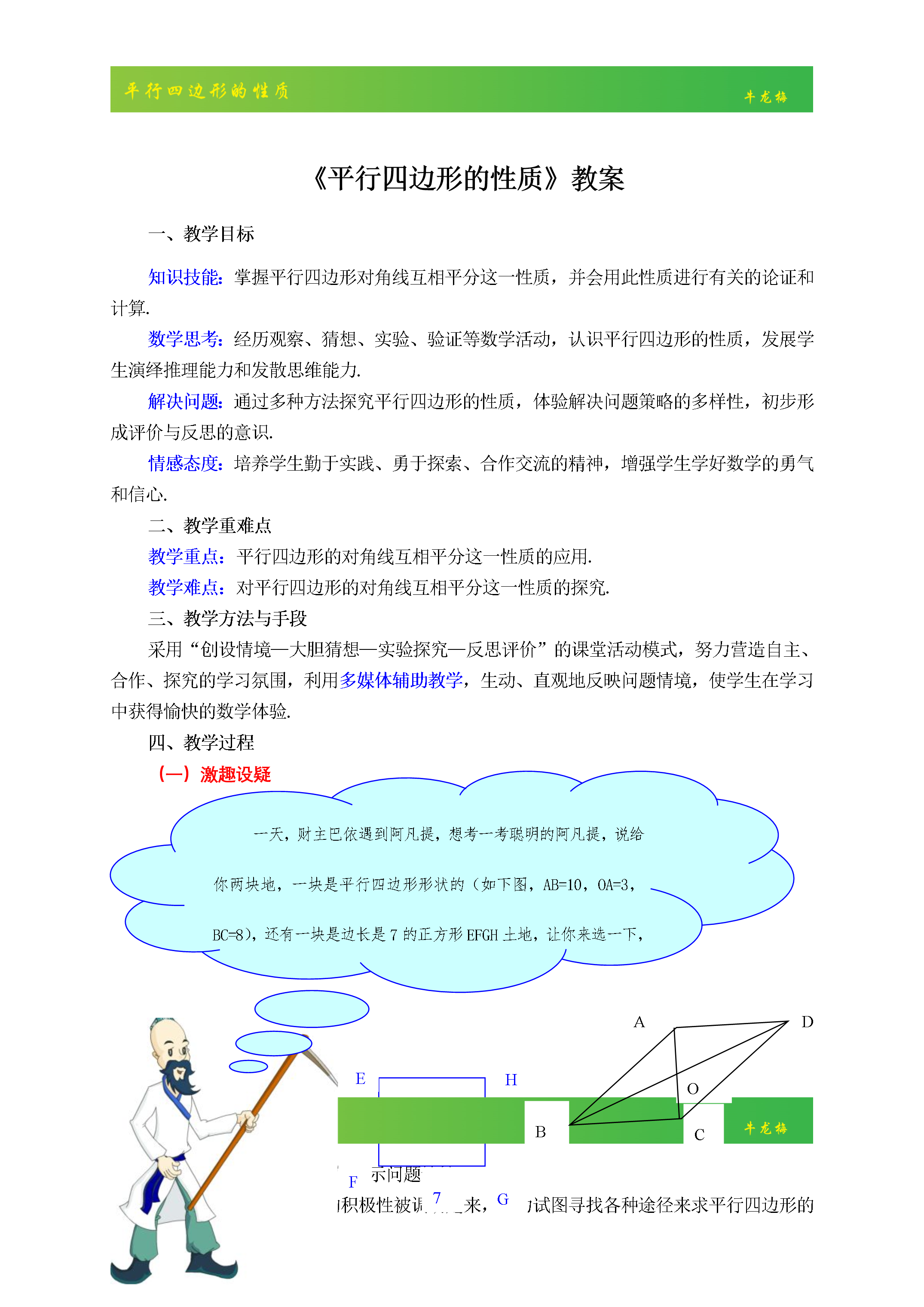
全国初中青年数学教师优秀课评比活动教案《平行四边形的性质》牡丹江市第四中学授课教师:黑龙江省牡丹江市第四中学牛龙梅E-mail:mdjsznlm@163.com邮编:157000二〇〇八年十一月《平行四边形的性质》教案一、教学目标知识技能:掌握平行四边形对角线互相平分这一性质并会用此性质进行有关的论证和计算.数学思考:经历观察、猜想、实验、验证等数学活动认识平行四边形的性质发展学生演绎推理能力和发散思维能力.解决问题:通过多种方法探究平行四边形的性质体验解决问题策略的多样性初步形成评价与反

黑龙江省牡丹江四中牛龙梅的上课教案.doc
全国初中青年数学教师优秀课评比活动教案《平行四边形的性质》牡丹江市第四中学授课教师:黑龙江省牡丹江市第四中学牛龙梅E-mail:mdjsznlm@163.com邮编:157000二〇〇八年十一月《平行四边形的性质》教案一、教学目标知识技能:掌握平行四边形对角线互相平分这一性质,并会用此性质进行有关的论证和计算.数学思考:经历观察、猜想、实验、验证等数学活动,认识平行四边形的性质,发展学生演绎推理能力和发散思维能力.解决问题:通过多种方法探究平行四边形的性质,体验解决问题策略的多样性,初步形成评价与反思的意

黑龙江省牡丹江四中牛龙梅的说课教案.doc
全国初中青年数学教师优秀课评比活动教案《平行四边形的性质》牡丹江市第四中学授课教师:黑龙江省牡丹江市第四中学牛龙梅E-mail:mdjsznlm@163.com邮编:157000二〇〇八年十一月《平行四边形的性质》说课教案尊敬的各位评委、老师:大家好!我是黑龙江省牡丹江市第四中学数学教师—牛龙梅,今天,我说课的内容是选自人教版新课标实验教材《数学》八年级下第十九章第一节第二课时《平行四边形的性质》.我设计的说课共分四大环节.一、设计理念《数学课程标准》指出:“新课程实施的基本点是促进学生全面、持续、和谐地

黑龙江省牡丹江四中牛龙梅说课教案说明.doc
第六届全国初中青年数学教师优秀课评比参评教案说明《平行四边形的性质》教案说明黑龙江省牡丹江市第四中学牛龙梅《平行四边形的性质》是人教版新课标实验教材《数学》八年级下第十九章第一节第二课时内容,为更好地把握这一课时内容,对本课时教案予以说明.一、授课内容的数学本质平行四边形是最基本的几何图形,也是“空间与图形”领域中研究的主要对象之一.平行四边形成为“四边形、平行四边形、特殊的平行四边形(矩形、菱形、正方形)”这一紧密联系的知识链上的桥梁和纽带。二、教学目标1、知识与技能:掌握平行四边形对角线互相平分这一性

周龙梅的教学设计(教案).doc
教学设计(教案)基本信息学科数学年级高一教学形式新授课教师周龙梅单位英德市第一中学课题名称对数函数的图像和性质学情分析1、学生从初中到高一年级接触到了一些函数和研究函数的一些方法。2、学生对于信息技术的使用有一定的熟练程度(主要指作函数图象)。3、学生在学习了反函数之后,有了研究新函数的一种新方法,因此,选择这节课让学生自主研究对数函数的性质。学生可以选择描点作图的方法来研究对数函数的图像与性质,也可以选择使用教学软件来研究函数的图像与性质,还可以通过研究指数函数反函数的方法来研究对数函数的图像和性质等。
