
拓展性题目.doc

一只****ua




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料
拓展性题目.doc
拓展题目应用拓展1:已知:如图分别以BM、CM为边向⊿BMC形外作等边三角形ABM、CDME、F、G、H分别为AB、BC、CD、DA中点。猜测四边形EFGH的形状;证明你的猜想;(3)三角形BMC形状的改变是否对上述结论有影响?分析:可以把图形分解成我们所熟悉的图形。四边形EFGH的形状是由线段AC、BD决定的。连结AC、BD⊿AMC与⊿BMD全等。所以AC=BD因此四边形EFGH是菱形。如下图所示⊿BMC形状的改变对上述结论没有影响。变式练习1:已知:如图分别以BM、CM为边向⊿BMC形外作等腰直角三角
拓展性题目.doc
拓展题目应用拓展1:已知:如图分别以BM、CM为边向⊿BMC形外作等边三角形ABM、CDME、F、G、H分别为AB、BC、CD、DA中点。猜测四边形EFGH的形状;证明你的猜想;(3)三角形BMC形状的改变是否对上述结论有影响?分析:可以把图形分解成我们所熟悉的图形。四边形EFGH的形状是由线段AC、BD决定的。连结AC、BD⊿AMC与⊿BMD全等。所以AC=BD因此四边形EFGH是菱形。如下图所示⊿BMC形状的改变对上述结论没有影响。变式练习1:已知:如图分别以BM、CM为边向⊿BMC形外作等腰直角三角

拓展性题目.doc
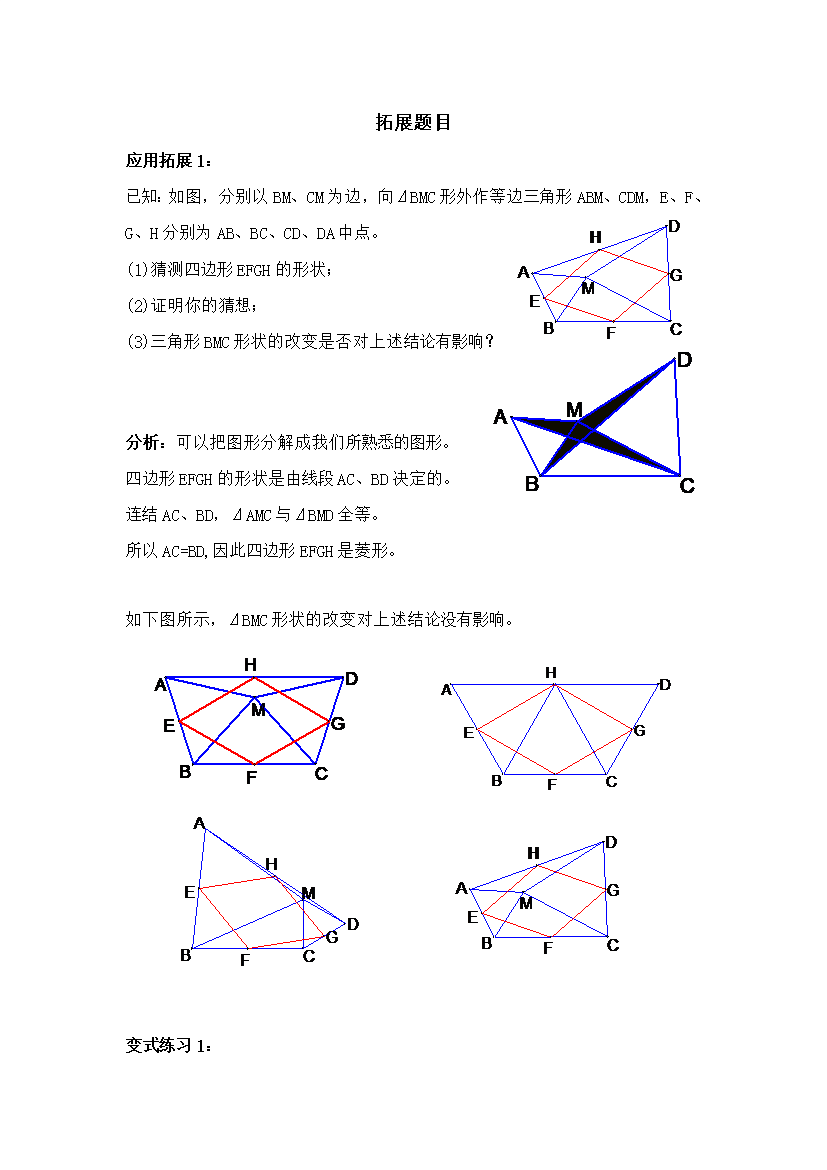
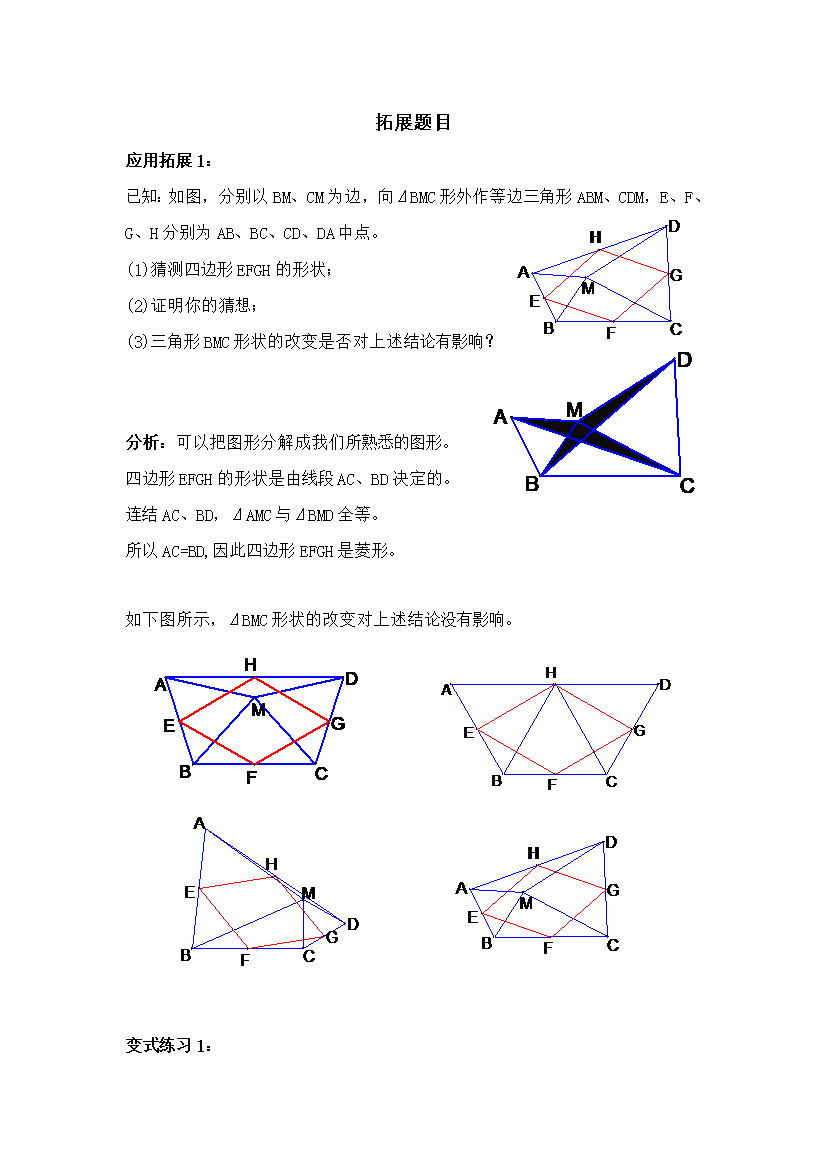
拓展题目应用拓展1:已知:如图,分别以BM、CM为边,向⊿BMC形外作等边三角形ABM、CDM,E、F、G、H分别为AB、BC、CD、DA中点。猜测四边形EFGH的形状;证明你的猜想;(3)三角形BMC形状的改变是否对上述结论有影响?分析:可以把图形分解成我们所熟悉的图形。四边形EFGH的形状是由线段AC、BD决定的。连结AC、BD,⊿AMC与⊿BMD全等。所以AC=BD,因此四边形EFGH是菱形。如下图所示,⊿BMC形状的改变对上述结论没有影响。变式练习1:已知:如图,分别以BM、CM为边,向⊿BMC形

拓展性题目.doc
拓展题目应用拓展1:已知:如图,分别以BM、CM为边,向⊿BMC形外作等边三角形ABM、CDM,E、F、G、H分别为AB、BC、CD、DA中点。猜测四边形EFGH的形状;证明你的猜想;(3)三角形BMC形状的改变是否对上述结论有影响?分析:可以把图形分解成我们所熟悉的图形。四边形EFGH的形状是由线段AC、BD决定的。连结AC、BD,⊿AMC与⊿BMD全等。所以AC=BD,因此四边形EFGH是菱形。如下图所示,⊿BMC形状的改变对上述结论没有影响。变式练习1:已知:如图,分别以BM、CM为边,向⊿BMC形

第六届恒拓杯题目.doc
双路低频信号发生及分析仪的设计制作难度系数:1.0一、任务设计并制作一个双路低频信号发生器,以及一个能对信号进行频域分析的仪器。电路结构框图示意图如图1所示。图1电路结构框图示意图二、要求1.基本要求两路信号均可程控选择输出正弦波、矩形波、三角波,频率可预置,范围为1000Hz到2000Hz,设置的步进值不大于10Hz,频率准确度不低于1%,且每路信号的波形及频率都可以单独预置。两路输出信号最大幅度不低于2.5V,幅度可预置,设置的步进值不大于100mv,且每路信号的幅度都可以单独预置。能产生两路频率相同
