
有关圆锥曲线轨迹方程的求法省名师优质课赛课获奖课件市赛课一等奖课件.ppt

可爱****乐多









亲,该文档总共23页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

有关圆锥曲线轨迹方程的求法省名师优质课赛课获奖课件市赛课一等奖课件.ppt
曲线与方程典例分析举一反三1.已知动点P到定点F(1,0)和直线x=3距离之和等于4,求点P轨迹方程.题型二利用定义或待定系数法求曲线方程【例2】已知圆:和圆:动圆M同时与圆及圆相外切.求动圆圆心M轨迹方程.解设动圆M与圆及圆分别外切于点A和点B,依据两圆外切充要条件,得,∵MA=MB,∴即这表明动点M到两定点、距离差是常数2.依据双曲线定义,动点M轨迹为双曲线左支(点M到距离大,到距离小),其中a=1,c=3,则.设点M坐标为(x,y),则其轨迹方程为(x≤1).学后反思处理本题关键是找到动点M满足条件

圆锥曲线与方程总结省名师优质课赛课获奖课件市赛课一等奖课件.ppt
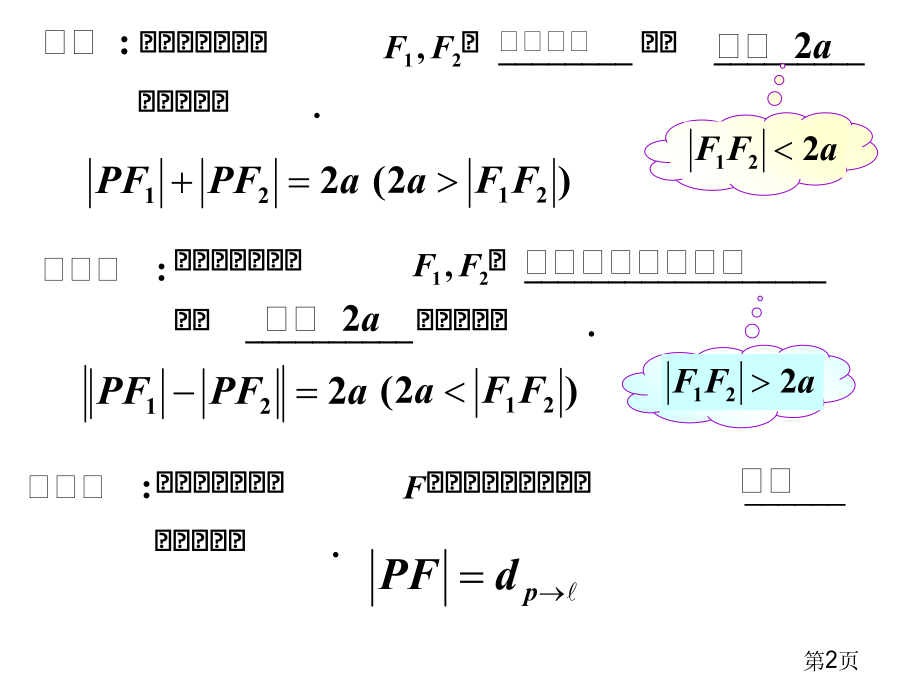
圆锥曲线与方程总结知识体系网络专题探究精讲(2)平面内满足||PF1|-|PF2||=2a(2a<|F1F2|)点P轨迹叫做双曲线,|PF1|-|PF2|=2a(2a<|F1F2|)表示焦点F2对应一支,定义可实现双曲线上点到两焦点距离相互转化.(3)平面内与一个定点F和一条定直线l(不经过点F)距离相等点轨迹叫做抛物线,定义可实现抛物线上点到焦点与到准线距离相互转化.【答案】B圆锥曲线性质(2)椭圆、双曲线有两条对称轴和一个对称中心,抛物线只有一条对称轴.(3)椭圆有四个顶点,对曲线有两个顶点,抛物线只

狄拉克方程省名师优质课赛课获奖课件市赛课一等奖课件.ppt
《高等量子力学》狄拉克方程内容提要一、波函数和薛定谔方程粒子在t时刻r点出现几率薛定谔方程薛定谔方程引入3.薛定谔方程(三维)二、克莱因-戈尔登方程3.自由粒子解德布罗意波保罗·狄拉克:英国理论物理学家,量子力学奠基者之一。薛定谔方程因为不是相对论性,它必定要向相对论扩展。克莱因-戈登方程就是第一个相对论性波动方程,然而却不能计算氢原子,且一直为负能态和负概率所困扰,所以长久不被物理学家所接收。狄拉克方程正是在这种困境中应运而生。它融合了狭义相对论、海森伯矩阵力学、薛定谔波动力学三方理论,能够计算氢原子光

有关健康的英语省名师优质课赛课获奖课件市赛课一等奖课件.ppt
ThebiggestwealthinlifeDoyouknowthemeaningof“health”?ImportanceofhealthTheimportanceofhealthTheimportanceofhealthTheimportanceofhealthPresentsituationThefourmajorfactorsaffectinghealthThefourmajorfactorsaffectinghealthEnvironmentalfactorsThefourmajorfactor

狄拉克方程1省名师优质课赛课获奖课件市赛课一等奖课件.ppt
《高等量子力学》狄拉克方程内容提要一、波函数和薛定谔方程粒子在t时刻r点出现几率薛定谔方程薛定谔方程引入3.薛定谔方程(三维)二、克莱因-戈尔登方程3.自由粒子解德布罗意波保罗·狄拉克:英国理论物理学家,量子力学奠基者之一。薛定谔方程因为不是相对论性,它必定要向相对论扩展。克莱因-戈登方程就是第一个相对论性波动方程,然而却不能计算氢原子,且一直为负能态和负概率所困扰,所以长久不被物理学家所接收。狄拉克方程正是在这种困境中应运而生。它融合了狭义相对论、海森伯矩阵力学、薛定谔波动力学三方理论,能够计算氢原子光
