内容提供者
几何中的最值问题12.ppt
2024-06-03
10金币
364KB
16页
仙人****88
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共16页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
几何中的最值问题12.ppt
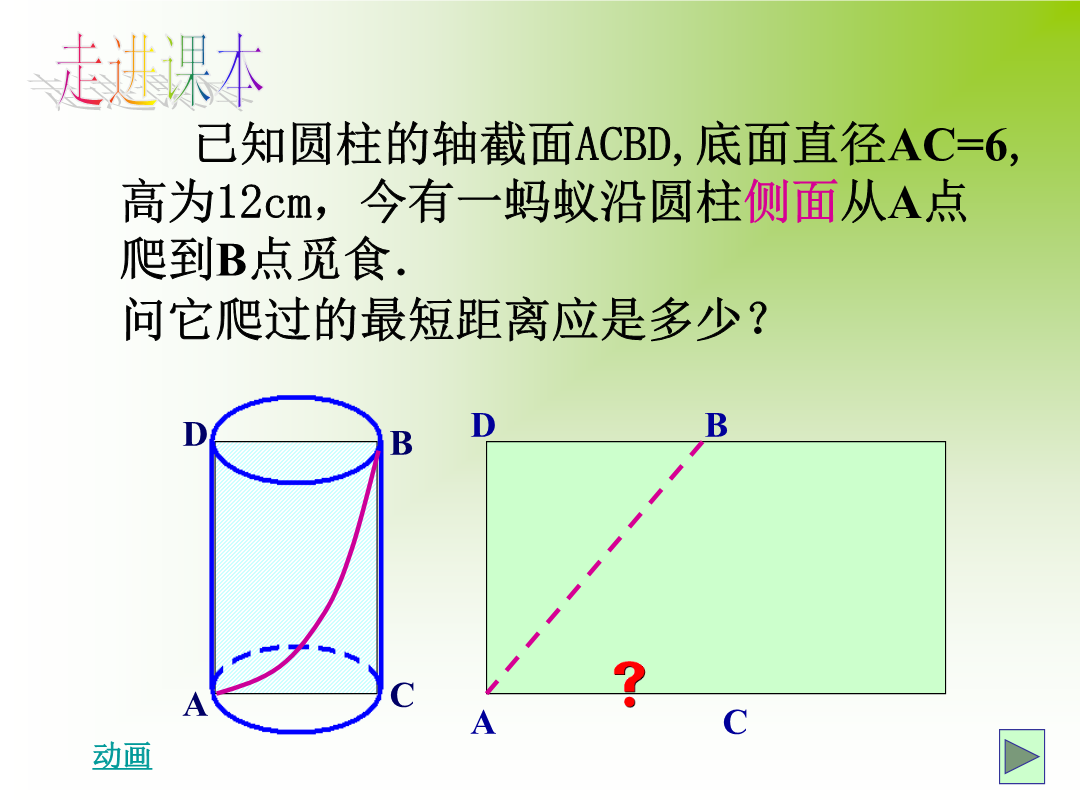
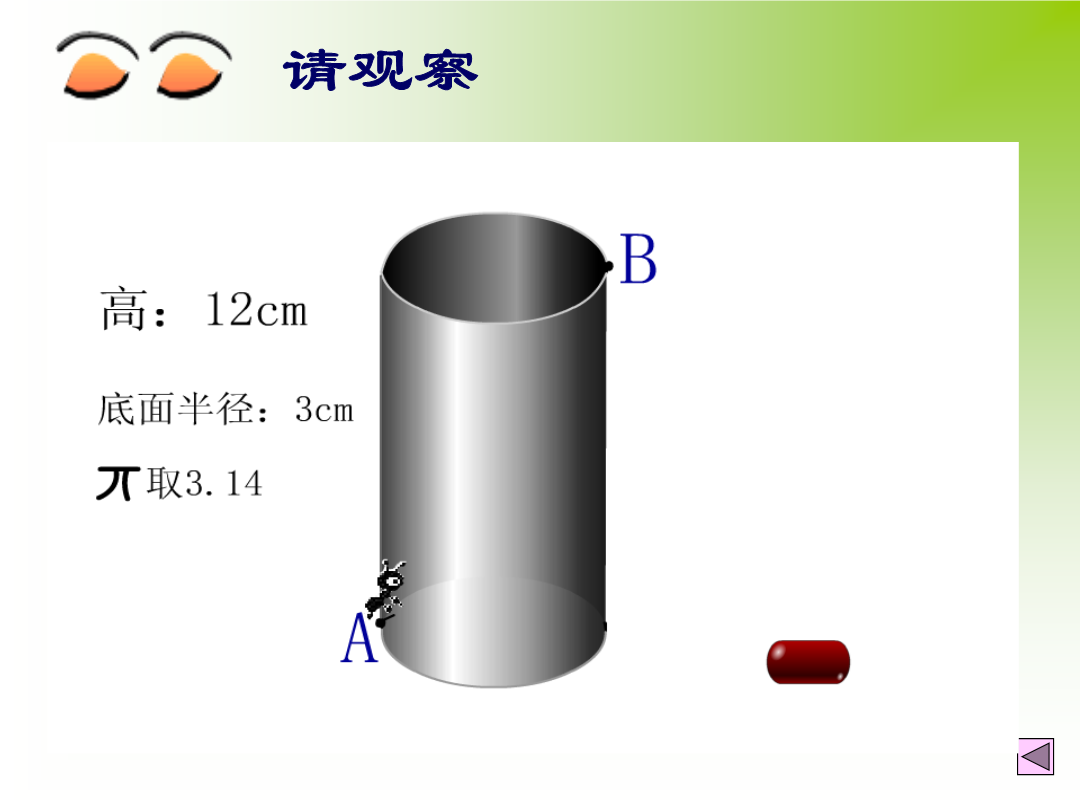
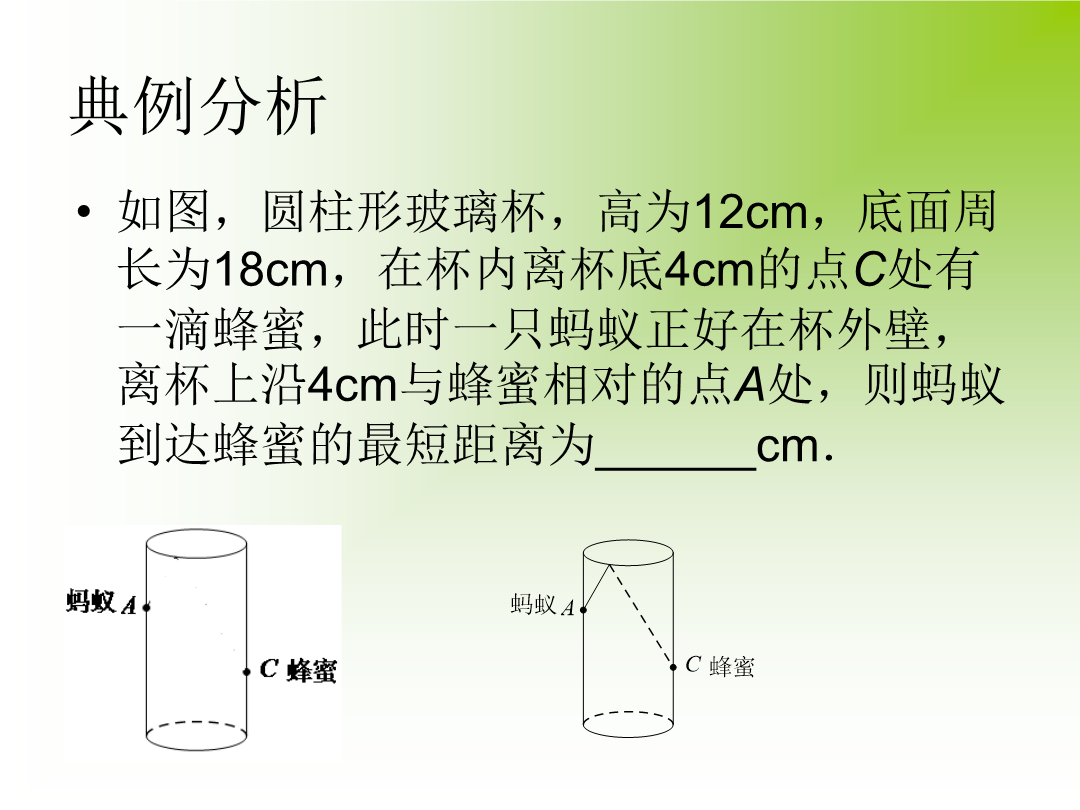
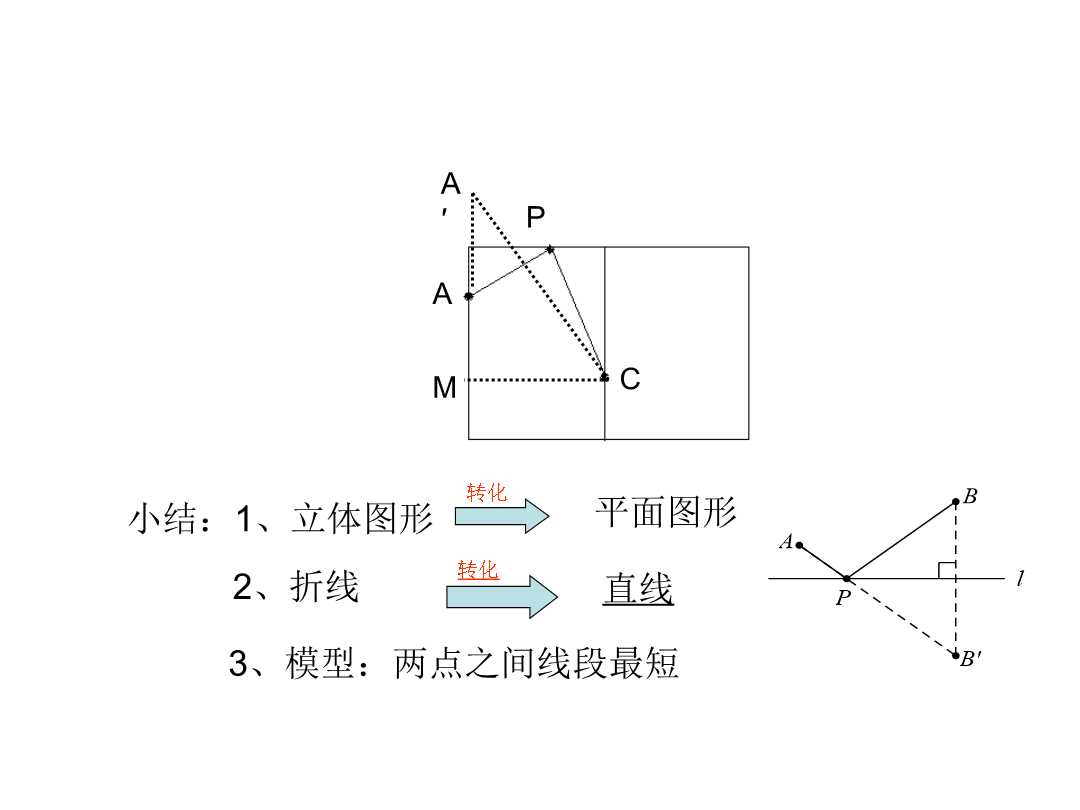
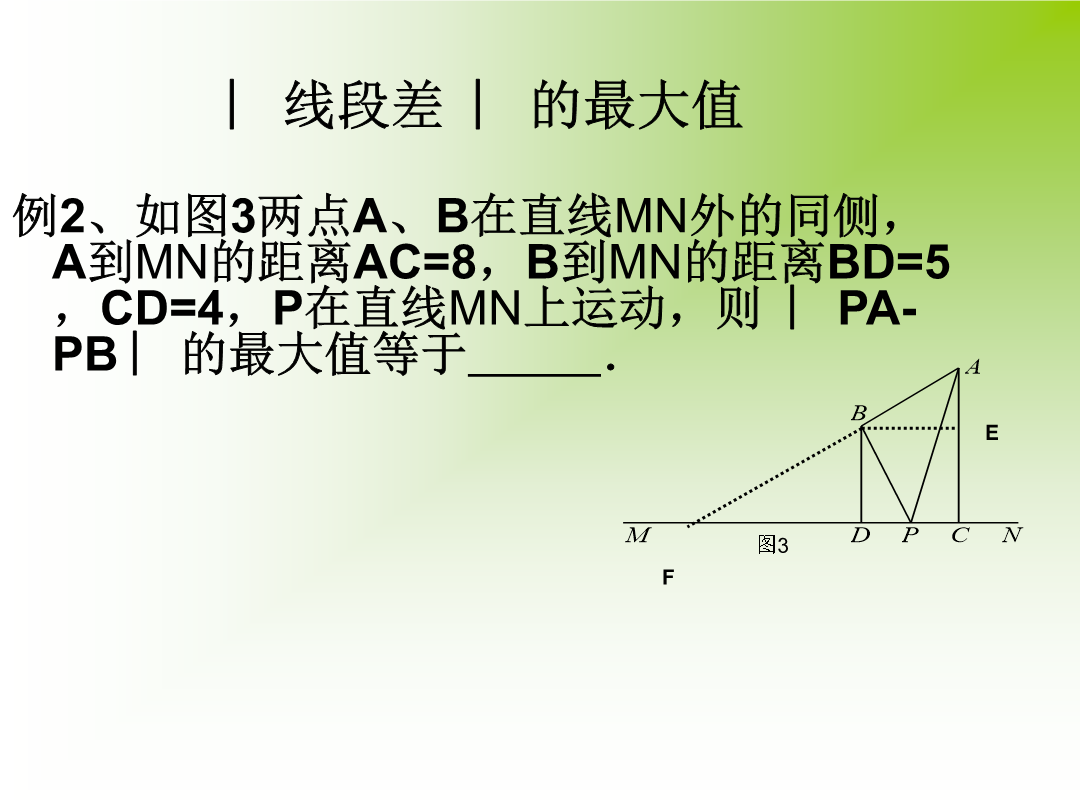
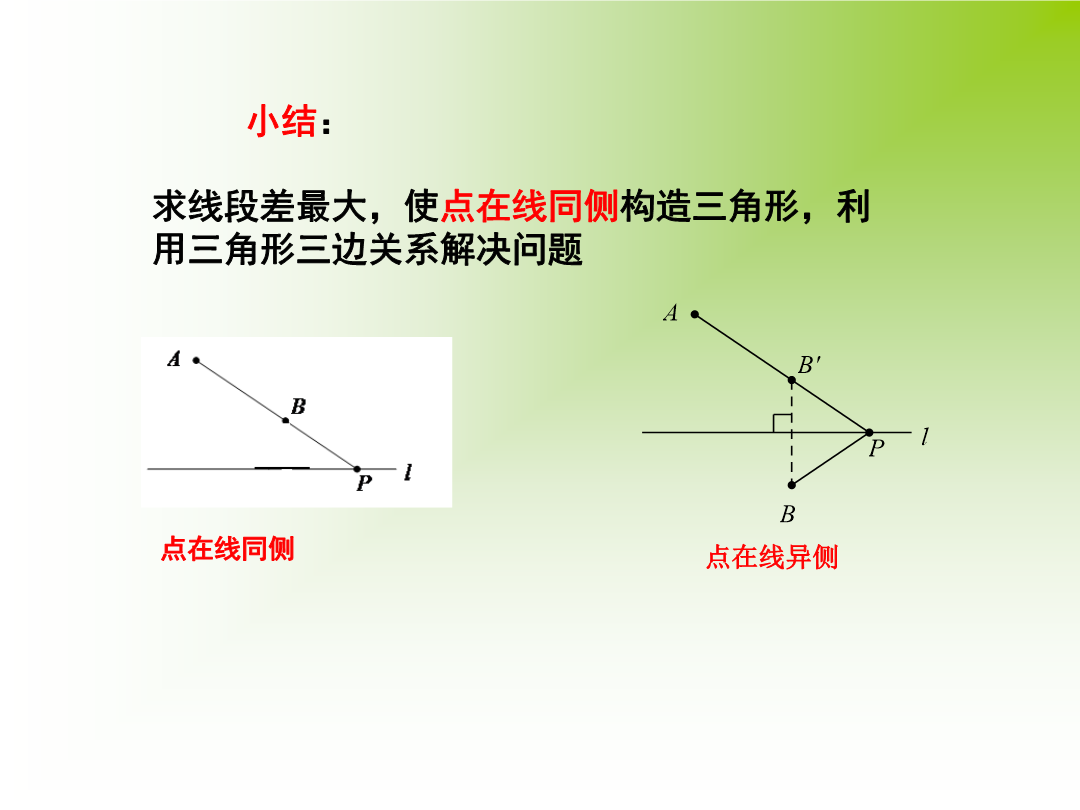
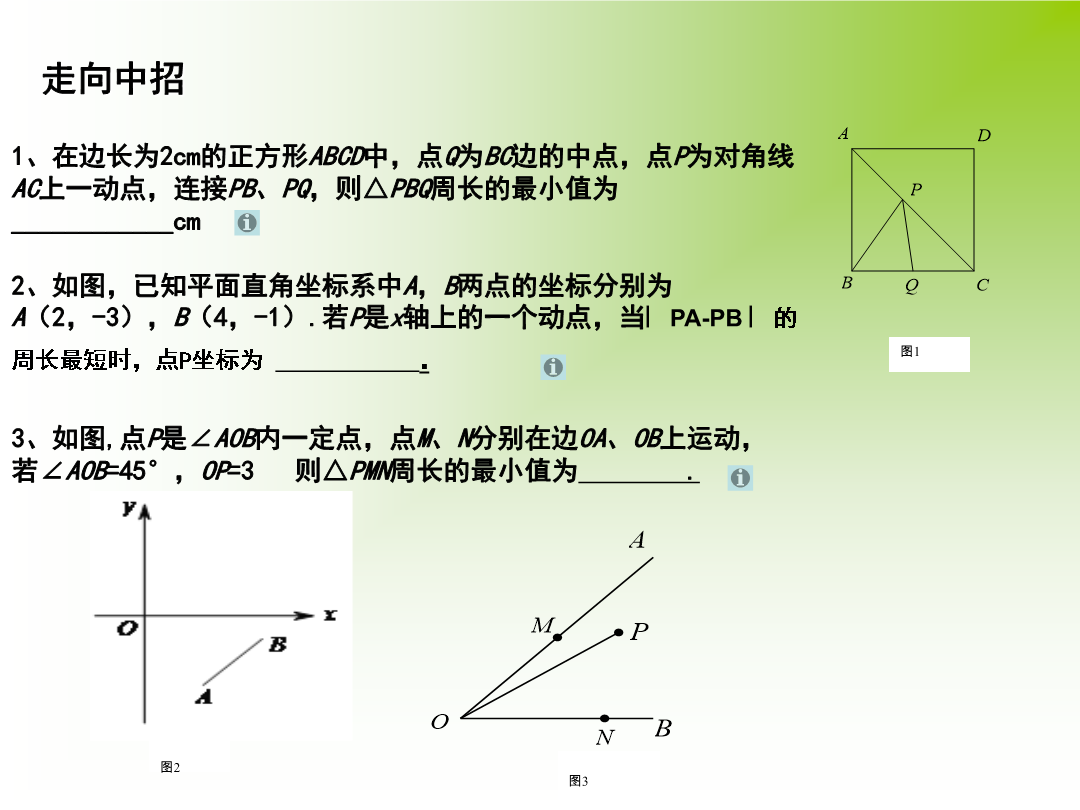
专题复习直击考点请观察典例分析例2、如图3两点A、B在直线MN外的同侧，A到MN的距离AC=8，B到MN的距离BD=5，CD=4，P在直线MN上运动，则︳PA-PB︳的最大值等于．求线段差最大，使点在线同侧构造三角形，利用三角形三边关系解决问题走向中招3、如图，在锐角△ABC中，∠BAC=45°，∠BAC的平分线交BC于点D，点M，N分别是AD和AB上的动点，则BM+MN的最小值为___________．4、如图，正方形ABCD的边长是4，∠DAC的平分线交DC于点E，若点P，Q分别是AD和AE上的动点，
2024-06-03
10
364KB
立体几何中的最值问题.doc
立体几何中的最值问题2007年普通高等学校招生全国统一考试新课程标准数学科考试大纲指出，通过考试，让学生提高多种能力，其中空间想象能力是对空间形式的观察、分析、抽象的能力.要在立体几何学习中形成。立体几何主要研究空间中点、线、面之间的位置关系，查遍近几年全国各省市的高考题中，与空间图形有关的线段、角、距离、面积、体积等最值问题常常在高考试题中出现，并且成增长趋势。下面举例说明解决这类问题的常用方法。策略一、公理与定义法SDCQBAPO例1、在正四棱锥S-ABCD中，SO⊥平面
2024-05-15
5
286KB
解析几何中的最值问题.ppt
解析几何中的最值问题解析几何中求最值问题的基本方法例1、椭圆上过点A（0，1）引椭圆的任意一条弦AB。设B（x，y）为椭圆上的一点。YD例3、直线L过点P（2，1），它在两坐标轴上的截距均为正值，若截距之和最小，求L的方程。例4、已知：实数x、y满足。求：的最值。例4、已知：实数x、y满足。求：的最值。A1(-1，2)例5、在直线x-y+1=0上找一点p，使p点到点A（1，0），B（3，0）的距离之和最小。A1(4，2)例6、2、已知方程:求：满足这个方程的实数对（x，y）中，的最值。用代数方法讨论几何问
2024-06-03
10
465KB
立体几何中的最值问题.doc
立体几何中的最值问题立体几何主要研究空间中点、线、面之间的位置关系，查遍近几年全国各省市的高考题中，与空间图形有关的线段、角、距离、面积、体积等最值问题常常在高考试题中出现，并且成增长趋势。下面举例说明解决这类问题的常用方法。策略一、公理与定义法例1、在正四棱锥S-ABCD中，SO⊥平面ABCD于O，SO=2，底面边长为，点P、Q分别在线段BD、SC上移动，SDCQBAPO则P、Q两点的最短距离为（）A.B.C.2D.1【解析】如图1，由于点P、Q分别在线段BD、SC上移动，
2024-06-10
10
274KB
平面几何中的最值问题.doc
平面几何中的最值问题在平面几何中，我们常常遇到各种求最大值和最小值的问题，有时它和不等式联系在在平面几何中，我们常常遇到各种求最大值和最小值的问题，有时它和不等式联系在一起，统称最值问题．如果把最值问题和生活中的经济问题联系起来，可以达到最经济、最节约和最高效率．下面介绍几个简例．在平面几何问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的面积、角的度数）的最大值或最小值问题，称为最值问题。最值问题的解决方法通常有两种：（1）应用几何性质：①三角形的三边关系：两边之和大于第三边，两边之
2024-06-16
10
92KB