预览加载中，请您耐心等待几秒...

解析几何中的最值问题.ppt

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共20页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

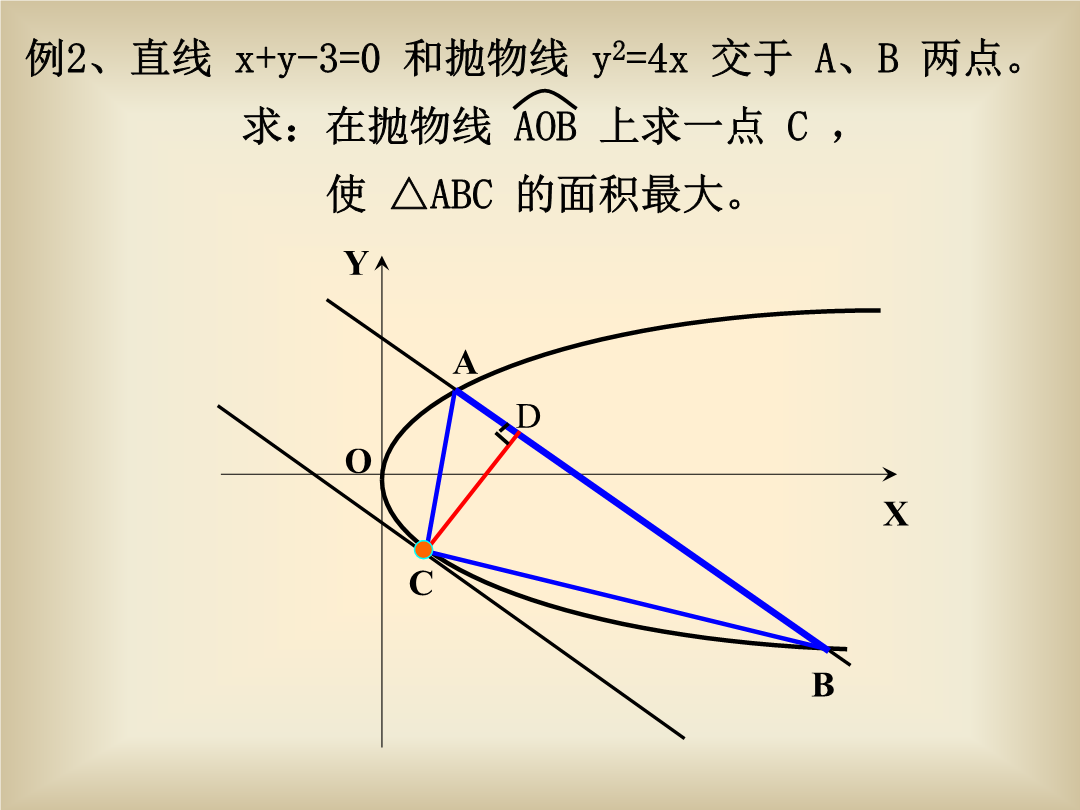
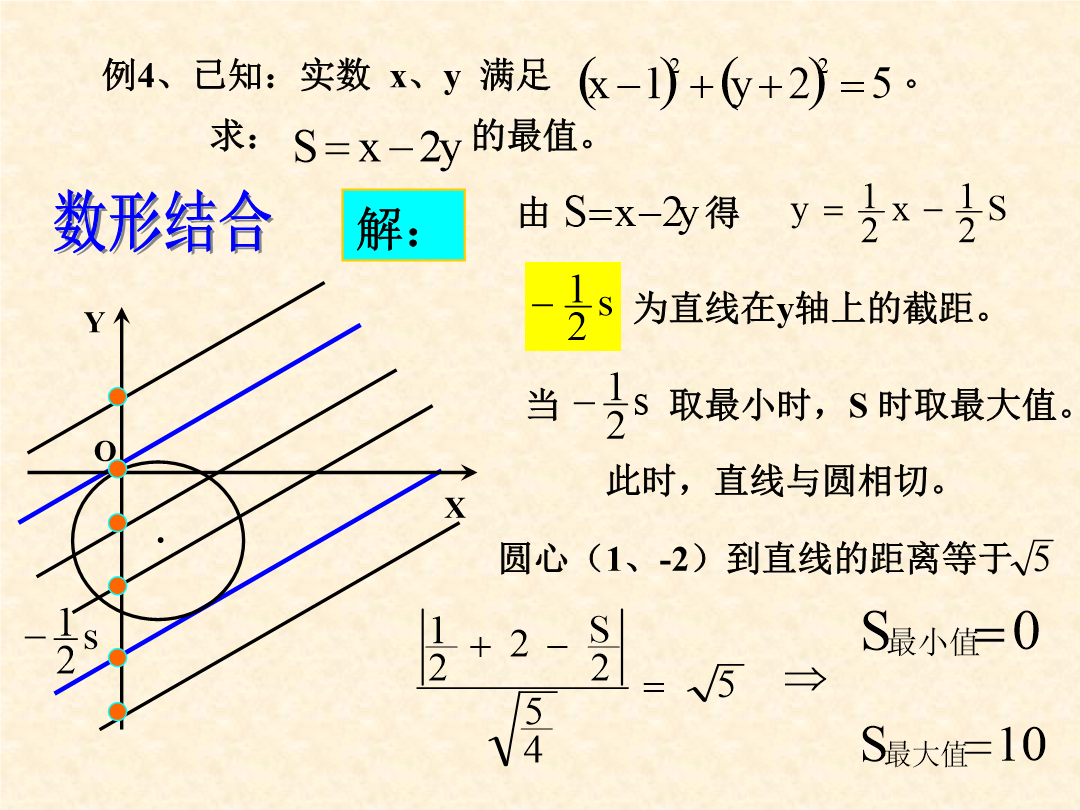
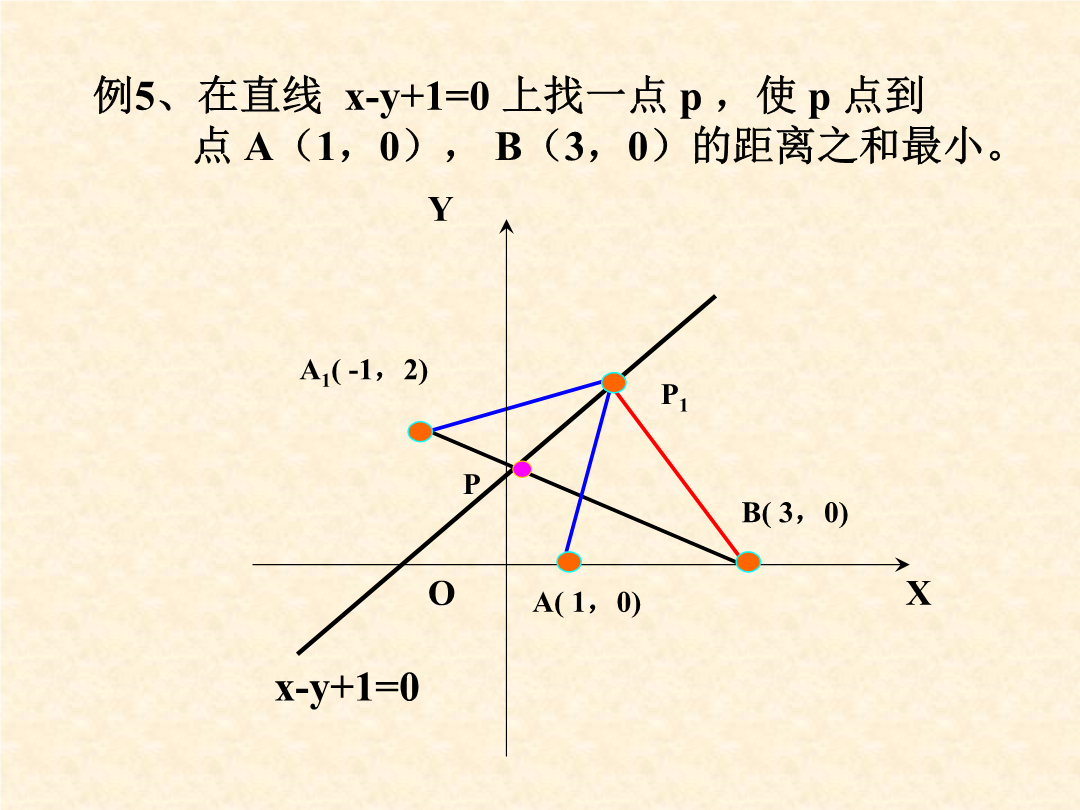
解析几何中的最值问题解析几何中求最值问题的基本方法例1、椭圆上过点A（0，1）引椭圆的任意一条弦AB。设B（x，y）为椭圆上的一点。YD例3、直线L过点P（2，1），它在两坐标轴上的截距均为正值，若截距之和最小，求L的方程。例4、已知：实数x、y满足。求：的最值。例4、已知：实数x、y满足。求：的最值。A1(-1，2)例5、在直线x-y+1=0上找一点p，使p点到点A（1，0），B（3，0）的距离之和最小。A1(4，2)例6、2、已知方程:求：满足这个方程的实数对（x，y）中，的最值。用代数方法讨论几何问题是解析几何的特点和手段。谢谢指导！Y2、已知方程:求：满足这个方程的实数对（x，y）中，的最值。提示：