
张量和应力张量优秀PPT.ppt

和蔼****娘子








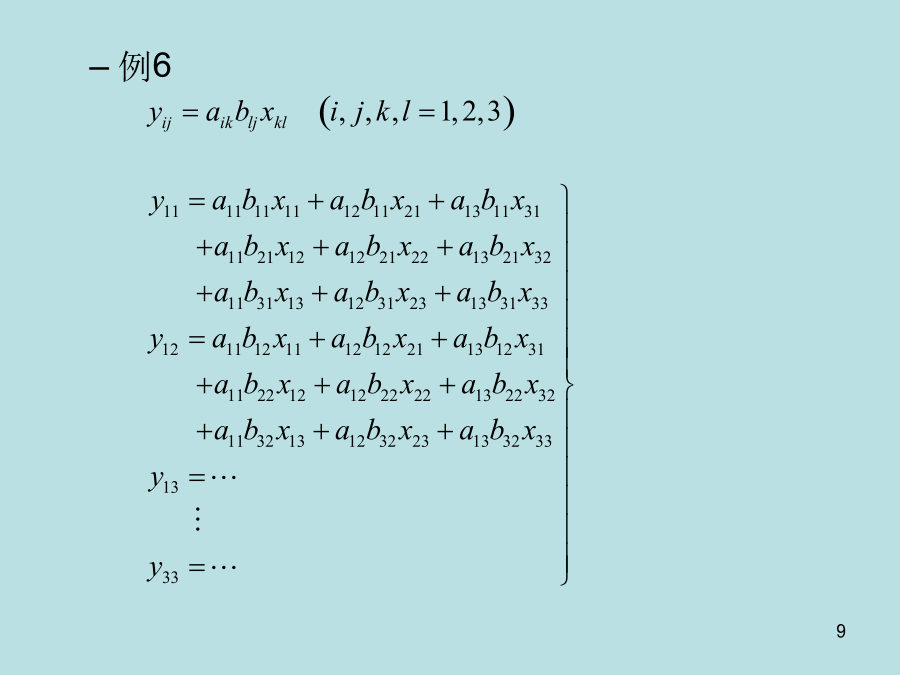

亲,该文档总共17页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

张量和应力张量优秀PPT.ppt
附录张量和应力张量1张量的基本概念1.1角标符号如果一个角标符号带有个m角标,每个角标取n个值,则该角标符号代表nm个元素。例σij(i,j=x,y,z)有32=9个元素(即九个应力分量)。1.2求和约定求和约定-合并例例1例2重复出现的角标称为哑标,不重复出现的角标称为自由标。自由标不包含求和的意思,但它可表示该表达式的个数。求和约定-展开例例1例2例3例4例5例61.3张量的基本概念物理量P在空间坐标系xi(i=1,2,3)中存在九个分量Pij(i,j=1,2,3);在新空间坐标系xk(k=1’,2’

张量和应力张量ppt课件.ppt
附录张量和应力张量1张量的基本概念1.1角标符号如果一个角标符号带有个m角标,每个角标取n个值,则该角标符号代表nm个元素。例σij(i,j=x,y,z)有32=9个元素(即九个应力分量)。1.2求和约定求和约定-合并例例1例2重复出现的角标称为哑标,不重复出现的角标称为自由标。自由标不包含求和的意思,但它可表示该表达式的个数。求和约定-展开例例1例2例3例4例5例61.3张量的基本概念物理量P在空间坐标系xi(i=1,2,3)中存在九个分量Pij(i,j=1,2,3);在新空间坐标系xk(k=1’,2’

张量和应力张量.ppt
1张量的基本概念1.1角标符号如果一个角标符号带有个m角标,每个角标取n个值,则该角标符号代表nm个元素。例σij(i,j=x,y,z)有32=9个元素(即九个应力分量)。1.2求和约定求和约定-合并例例1例2重复出现的角标称为哑标,不重复出现的角标称为自由标。自由标不包含求和的意思,但它可表示该表达式的个数。求和约定-展开例例1例2例3例4例5例61.3张量的基本概念物理量P在空间坐标系xi(i=1,2,3)中存在九个分量Pij(i,j=1,2,3);在新空间坐标系xk(k=1’,2’,3’)中存在九个

张量和应力张量学习教案.pptx
会计学1张量的基本概念1.1角标符号如果一个角标符号带有个m角标,每个角标取n个值,则该角标符号代表nm个元素。例σij(i,j=x,y,z)有32=9个元素(即九个应力分量)。1.2求和约定求和约定-合并例例1例2重复出现的角标称为哑标,不重复出现的角标称为自由标。自由标不包含求和的意思,但它可表示该表达式的个数。求和约定-展开例例1例2例3例4例5例61.3张量的基本概念物理量P在空间坐标系xi(i=1,2,3)中存在九个分量Pij(i,j=1,2,3);在新空间坐标系xk(k=1’,2’,3’)中存

应力张量应变张量和应力应变关系.pptx
§5-1应力分量旳坐标变换应力张量§5-2主应力应力张量不变量§5-3最大剪应力§5-4笛卡尔张量基础§5-5物体内无限邻近两点位置旳变化转动张量§5-6应变旳坐标变换应变张量§5-7主应变应变张量不变量§5-8广义Hooke定律旳一般形式§5-9弹性体变形过程中旳能量§5-10应变能和应变余能§5-11各向异性弹性体旳应力-应变关系§5-12各向同性弹性体应力-应变关系§5-13各向同性弹性体各弹性常数间旳关系分别称为应力张量旳第一、第二、第三不变量。则能量守恒定律指出:封闭系统中总能量旳增长(涉及动能
